Импульс тела. Закон сохранения импульса в природе и технике

План ответа

1. Импульс тела. 2. Закон сохранения импуль­са. 3. Применение закона сохранения импульса. 4. Реактивное движение.

Существуют величины, которые могут сохра­няться при взаимодействии тел. Такими величинами являются энергия и импульс.

Импульсом тела называют векторную физи­ческую величину, являющуюся количественной ха­рактеристикой поступательного движения тел. Им­пульс обозначается р. Единица измерения импульса

Р — кг • м/с. Импульс тела равен произведению мас­сы тела на его скорость: р = mv. Направление векто­ра импульса р совпадает с направлением вектора скорости тела v (рис. 4).

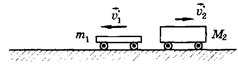
Рис. 4

Для импульса тел выполняется закон сохране­ния.Имеет вид m₁v₁ + т₂v₂ = m₁v₁' + т₂v₂' где т₁ и

т₂ — массы тел, а v₁ и v₂, — скорости до взаимодей­ствия, v₁' и v₂' — скорости после взаимодействия. Эта

формула и является математическим выражением закона сохранения импульса:импульс замкнутой физической системы сохраняется при любых вза­имодействиях, происходящих внутри этой системы.

В механике закон сохранения импульса и за­коны Ньютона связаны между собой. Если на тело массой т в течение времени t действует сила и ско­рость его движения изменяется от v₀ до v, то уско­рение движения a тела равно a = (v - v₀)/t. На осно­вании второго закона Ньютона для силы F можно записать F = та = m(v - v₀)/t, отсюда следует

Ft = mv - mv₀.

Ft — векторная физическая величина, харак­теризующая действие на тело силы за некоторый промежуток времени и равная произведению силы на время t ее действия, называетсяимпульсом силы.

Единица импульсав СИ — Н • с.

Закон сохранения импульса лежит в основе реактивного движения.Реактивное движение — это такое движение тела, которое возникает после отде­ления от тела его части.

Большая заслуга в развитии теории реак­тивного движения принадлежит К. Э. Циолковскому.

Он разработал теорию полета тела переменной массы (ракеты) в однородном поле тяготения и рас­считал запасы топлива, необходимые для преодоле­ния силы земного притяжения; основы теории жид­костного реактивного двигателя, а так же элементы его конструкции; теорию многоступенчатых ракет, причем предложил два варианта: параллельный (несколько реактивных двигателей работают одно­временно) и последовательный (реактивные двигате­ли работают друг за другом).В основе движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатиц) также лежит реактив­ный принцип.

Билет №5

Закон всемирного тяготения. Гравитационное поле. Сила тяжести. Вес тела.

Исаак Ньютон выдвинул предположение, что между любыми телами в природе существуют силы взаимного притяжения. Эти силы называют силами гравитации, или силами всемирного тяготения. Сила всемирного тяготения проявляется в Космосе, Солнечной системе и на Земле. Ньютон обобщил законы движения небесных тел и выяснил, что сила F равна:

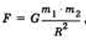
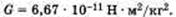
m₁ и т₂ -массы взаимодействующих тел, R — расстояние между ними, G — коэффициент пропорциональности, который называется гравитационной постоянной. Численное значение гравитационной постоянной опытным путем определил Кавендиш, измеряя силу взаимодействия между свинцовыми шарами. В результате закон всемирного тяготения звучит так: между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки.

Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах (или если хотя бы масса одного из тел велика). Закон же всемирного тяготения выполняется только для материальных точек и шаров (в этом случае за расстояние принимается расстояние между центрами шаров).

Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свободного падения. В соответствии со вторым законом Ньютона g = F_тяж*m следовательно, F_тяж = mg. Сила тяжести всегда направлена к центру Земли. В зависимости от высоты h над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с2.
В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете (рис. 1). Вес тела обозначается Р. Единица веса - Н. Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры.

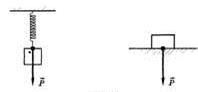
Если тело свободно падает, то в этом случае P = (g- g)m = 0. Состояние тела, в котором его вес равен нулю, называют невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением, поэтому в корабле наблюдается состояние невесомости.

Билет №6

Энергия. Потенциальная и кинетическая энергия.

Движущиеся тела имеют способность выполнять работу в случае изменения скорости. Энергия, которой обладает тело вследствие своего движения, называется кинетической энергией.

Часть механической энергии, обусловленная движением тела, называется кинетической энергией - Ек.

Зависимость кинетической энергии от массы движущегося тела и его скорости

Кинетическая энергия тела, движущегося с определенной скоростью, равна работе, которую нужно выполнить, чтобы придать неподвижному телу эту скорость. Пусть до неподвижного тела массой m приложена постоянную силу F. Тогда Eк = А = Fs, где s- модуль перемещения. Подставляя в эту формулу выражения F = mа и s = v²/2a, получим: кинетическая энергия тела массой m, движущегося со скоростью v, выражается формулой Eк = mv²/2.

Часть механической энергии, которая определяется взаимным расположением тел, которые взаимодействуют, называется потенциальной энергией - Еп.

Например, если сила тяжести выполняет работу во время падения груза вниз, система «поднятый груз и Земля» имеет потенциальную энергию.

Обозначим изменение потенциальной энергии 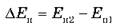, где индексом 1 обозначены начальное состояние системы, а индексом 2 - конечный.

Если во время изменения взаимного расположения тел система выполняет положительную работу, ее потенциальная энергия уменьшается, а если система выполняет отрицательную работу, ее потенциальная энергия увеличивается.

Изменение потенциальной энергии ΔЕп и А работа, выполненная системой, связаны соотношением:

ΔЕп = -A.

Из этой формулы следует, что физический смысл имеет только изменение потенциальной энергии: она измеряется работой, что ее исполнила система. Выбор нулевого уровня потенциальной энергии определяется соображениями удобства для решения каждой конкретной задачи.

а) Потенциальная энергия груза, поднятого над землей. Во время поднятия груза массой m на высоту h работа выполняется mgh, поэтому потенциальная энергия системы «груз и Земля» увеличивается на mgh. Выберем как нулевой уровень потенциальной энергии состояние системы, когда груз находится на поверхности земли. Тогда Еп = mgh.

б) Потенциальная энергия деформированной пружины. Потенциальная энергия деформированной пружины равна работе, которую надо выполнить, чтобы деформировать пружину. А = kx²/2, где k - жесткость пружины, x - ее удлинение. Следовательно, потенциальная энергия деформированной пружины Eп = kx²/2.

Билет №7