Энергия гармонических колебаний.

Гармонические колебания

Важным частным случаем периодических колебаний являются гармонические колебания, т.е. такие изменения физической величины, которые идут по закону

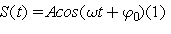
где 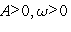. Из курса математики известно, что функция вида (1) меняется в пределах от А до -А , и что наименьший положительный период у нее 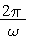. Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом .

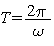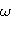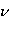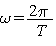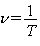Не следует путать циклическую частоту и частоту колебаний . Между ними простая связь. Так как , а , то .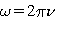

Величина 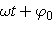называется фазой колебания. При t=0 фаза равна 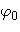, потому 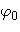называют начальной фазой.

Отметим, что при одном и том же t:

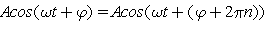
где 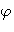- начальная фаза .Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точнотью до 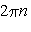. Поэтому из множества возможных значений начальной фазы выбирается обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это необязательно. Например, дано колебание 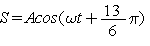, то его удобно записать в виде 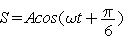и работать в дальнейшем с последним видом записи этого колебания.

Можно показать, что колебания вида:

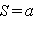
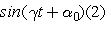
где 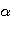и 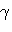могут быть любого знака, с помощью простых тригонометрических преобразований всегда приводится к виду (1), причем 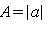, , 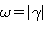а 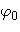не равна 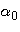, вообще говоря. Таким образом, колебания вида (2) являются гармоническими с амплитудой 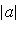и циклической частотой 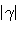. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.

Пусть требуется показать, что колебание

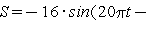
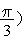
будет гармоническим и найти амплитуду 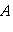, циклическую частоту 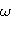, период 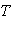и начальную фазу 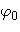. Действительно,

-

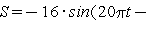
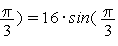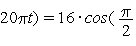
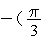
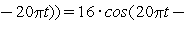
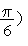
Видим, что колебание величины S удалось записать в виде (1). При этом , .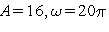

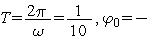
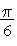Попробуйте самостоятельно убедится, что

.

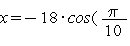
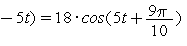
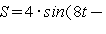
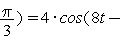
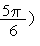Естественно, что запись гармонических колебаний в форме (2) ничем не хуже записи в форме (1), и переходить в конкретной задаче от записи в данной форме к записи в другой форме обычно нет необходимости. Нужно только уметь сразу находить амплитуду, циклическую частоту и период, имея перед собой любую форму записи гармонического колебания.

Иногда полезно знать характер изменения первой и второй производных по времени от величины S, которая совершает гармонические колебания (колеблется по гармоническому закону). Если 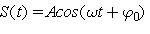, то дифференцирование S по времени t дает 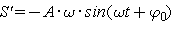, 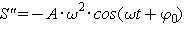. Видно, что S' и S'' колеблются тоже по гармоническому закону с той же циклической частотой 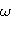, что и величина S, и амплитудам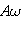и и 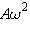, соответственно. Приведем пример.

Пусть координата x тела, совершающего гармонические колебания вдоль оси x, изменяется по закону 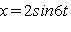, где х в сантиметрах, время t в секундах. Требуется записать закон изменения скорости и ускорения тела и найти их максимальные значения. Для ответа на поставленный вопрос заметим, что первая производная по времени от величины х есть проекция скорости тела на ось х, а вторая производная х есть проекция ускорения на ось х: 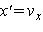, 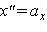. Продифференцировав выражение для х по времени, получим 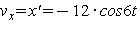, 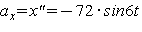. Максимальные значения скорости и ускорения : .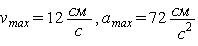