Линии и трубки тока. Уравнение неразрывности струи
Гидродинамика – раздел гидроаэромеханики, в котором изучается движение несжимаемых жидкостей и их взаимодействие с твердыми телами.
В гидродинамике различают понятия идеальной и реальной жидкостей.
Идеальной называют воображаемую жидкость, лишенную вязкости и теплопроводности.
Для описания движения жидкости используют понятия «линия тока» и «трубка тока». При установившемся течении все частицы жидкости движутся по определенным траекториям с определенными скоростями.
Линия тока – это линия, в каждой точке которой вектор скорости частицы направлен по касательной (рис.1.).
Понятие линии тока позволяет изобразить поток жидкости графически. Условились проводить линии тока так, чтобы густота их была пропорциональна величине скорости в данном месте. Там, где линии проведены гуще, скорость течения больше и наоборот (рис.2).
В общем случае величина и направление вектора 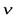 в каждой точке пространства могут изменяться со временем, поэтому и картина линий тока будет меняться.
в каждой точке пространства могут изменяться со временем, поэтому и картина линий тока будет меняться.
Возможно течение, при котором любая частица жидкости проходит данную точку пространства с одной и той же скоростью. Течение принимает стационарный характер.
Стационарным называют такое течение, при котором в данной точке вектор скорости 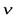 не изменяется с течением времени.
не изменяется с течением времени.
Трубка тока – это объем жидкости, ограниченный линиями тока (рис.3).
S1 и S2 – два произвольных сечения трубки тока;
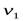 и
и 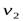 – скорости течения жидкости в этих сечениях.
– скорости течения жидкости в этих сечениях. 
Рассмотрим сечение S трубки тока, перпендикулярное скорости 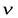 (рис.4).
(рис.4).
За время 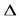 t через сечение S пройдут все частицы, расстояние которых от S в начальный момент времени не превышает расстояние l = v
t через сечение S пройдут все частицы, расстояние которых от S в начальный момент времени не превышает расстояние l = v 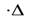 t. Поэтому за время
t. Поэтому за время 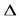 t через сечение S пройдет объем жидкости
t через сечение S пройдет объем жидкости
V = S 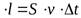
 (1)
(1)
А за единицу времени объем
Q = 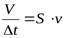 (1)
(1) 
Теорема о неразрывности струи: при стационарном течении идеальной жидкости произведение площади поперечного сечения S трубки тока на скорость сечения жидкости v есть величина постоянная для любого сечения трубки тока, т.е.
S × v =const
Для доказательства возьмем трубку тока настолько тонкую, что в каждом сечении скорость можно считать постоянной (рис.5.) Жидкость абсолютно несжимаема, т.е. ее плотность во всем объеме жидкости одинакова и неизменна. Тогда количество жидкости между сечениями S  и S
и S 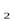 будет оставаться постоянным, а
будет оставаться постоянным, а
Рис. 5
это возможно только при условии, что объем
жидкости, протекающей через сечение S 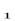 и S
и S 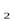 за время
за время 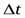 одинаковы, т.е.v
одинаковы, т.е.v 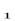 =v
=v 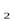 или, учитывая (1), можно записать
или, учитывая (1), можно записать
S 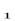 v
v 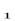
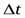 = S
= S 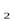 v
v 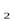
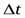 (2)
(2)
Приведенные рассуждения справедливы для любой пары сечений трубки тока, поэтому величина S×v для любого сечения трубки тока должна быть одна и та же.
Условие неразрывности струи применимо и к реальным жидкостям и газам, если их сжимаемостью можно пренебречь.
На рис.4 буквами р 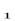 и р
и р 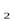 обозначены статические давления (давления напора) по обе стороны выделенного объема жидкостиV = S×l.
обозначены статические давления (давления напора) по обе стороны выделенного объема жидкостиV = S×l.
Чтобы скорость течения была направлена, как показано на рисунке, необходимо выполнение условия р 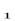 >р
>р 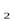 .
.
Тогда работа А по перемещению выбранного нами объема жидкости будет совершаться за счет разности сил давления F 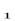 - F
- F 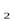 = р
= р 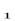 S - р
S - р 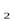 S
S 
А= 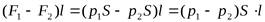

Учитывая, что 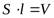 , можно записать
, можно записать
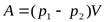 . (3)
. (3)
29. Рассмотрим трубку тока, расположенную наклонно в поле тяготения (рис.6). Выберем два произвольных сечения 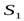 и
и 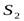 , находящихся на разных высотах по отношении к линии горизонта,
, находящихся на разных высотах по отношении к линии горизонта, 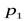 и
и 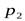 статические давления соответственно слева от сечения
статические давления соответственно слева от сечения 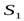 и справа от сечения
и справа от сечения 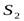 . Допустим, что
. Допустим, что 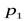 >
> 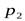 . Полная энергия некоторой массы
. Полная энергия некоторой массы 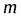 жидкости слагается из кинетической энергии
жидкости слагается из кинетической энергии 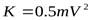 и
и
потенциальной энергии 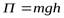 . Поэтому можно записать
. Поэтому можно записать 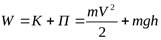 .
.
ля горизонтальной трубки тока 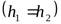 уравнение (6) принимает вид
уравнение (6) принимает вид
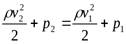 (9)
(9)
или
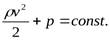 (10)
(10)
Формула Торричелли
Закон Торричелли показывает, что при истечении идеальной нестискувальнои жидкости из щели в боковой стенке или на дне сосуда жидкость приобретает скорость тела, падающего с определенной высоты. С помощью этого можно вычислить максимальный уровень утечки жидкости из сосуда. Для подтверждения можно воспользоваться законом Бернулли, выведя из него формулу Торричелли: ρgh + p 0 = (pV 2) / 2 + p 0, где p0 - атмосферное давление, h - высота столба жидкости в сосуде, V - скорость истечения жидкости. Отсюда V = √ 2gh.
31. Вязкость (внутреннее трение) —это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.
Сила внутреннего трения F тем больше, чем больше рассматриваемая площадь поверхности слоя S (рис. 52), и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою 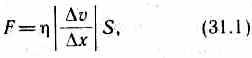
36. -----------------------------------
37. Термодинамическое равновесие
Утверждается, что любая замкнутая термодинамическая система, для которой внешние условия остаются неизменными, с течением времени переходит в равновесное состояние, в котором прекращаются все макроскопические процессы. Внешние параметры – это величины, определяемые положением не входящих в систему тел - (объем, магнитная индукция, напряженность электрического поля)
Внешние параметры являются функциями координат внешних тел.
Внутренние параметры – это величины, определяемые совокупным
движением и распределением в пространстве входящих в систему частиц
(температура, давление, внутренняя энергия, плотность, поляризованность,
намагниченность)
