Одномерные течения жидкостей и газов

Ю.В.Зуев

Одномерные течения жидкостей и газов

Допущено

Учебно-методическим объединением высших учебных

заведений Российской Федерации по образованию в

области авиации, ракетостроения и космоса в

качестве учебного пособия для студентов высших

учебных заведений, обучающихся по направлению

подготовки дипломированного специалиста 652200 —

«Двигатели летательных аппаратов»

Москва

Издательство МАИ

ББК 16.3.4.1

Зуев Ю.В. Одномерные течения жидкостей и газов: Учебное посо­бие. — М.: Изд-во МАИ, 2004. — 80с: ил.

ISBN 5-7035-1391-х

Дается описание одномерных течений жидкостей и газов, изуче­ние которых предусмотрено стандартной программой дисциплины «Механика жидкости и газа». Рассматриваются сверхзвуковые тече­ния со скачками уплотнения и с непрерывным увеличением скорос­ти (течение Прандтля-Майера). Излагаются одномерные модели, ко­торые могут быть использованы для расчета параметров простран­ственных течений в каналах. Приводится описание лабораторных работ, выполнение которых позволяет студентам закрепить теорети­ческие знания на практике.

Для студентов, обучающихся по специальностям 130200 — «Авиационные двигатели и энергетические установки», 130400 — «Ракетные двигатели», 130500 — «Электроракетные двигатели и энергетические установки» и 131500 — «Авиационная и космическая теплотехника» направления 652200 «Двигатели летательных аппара­тов».

Рецензенты: кафедра аэродинамики, конструкции и прочности ЛА МГТУ ГА (зав. кафедрой В.Г. Ципенко); К.А. Малиновский

ISBN 5-7035-1391-х ©Московский авиационный институт

(государственный технический университет), 2004

© Ю.В. Зуев, 2004

Предисловие

Государственным образовательным стандартом высшего профессионального образования по направлению 652200 "Двигатели летательных аппаратов" для специальностей 130200 - "Авиационные двигатели и энергетические установки", 130400 - "Ракетные двигатели", 130500 - "Электроракетные двигатели и энергетические установки" и 131500 - "Авиационная и космическая теплотехника" в качестве одной из общепрофессиональных дисциплин предусмотрена дисциплина "Механика жидкости и газа".

Задачей, которая ставится перед студентами, осваивающими эту дисциплину, является получение базовых знаний для более детального изучения в последующих специальных дисциплинах процессов, протекающих в двигателях различных типов. Программа дисциплины "Механика жидкости и газа" предусматривает чтение лекций, проведение практических занятий и выполнение лабораторных работ.

В пособии приводится описание одномерных течений жидкостей и газов, изучение которых предусмотрено стандартной программой дисциплины "Механика жидкости и газа". Рассматриваются сверхзвуковые течения с косыми скачками уплотнения и с непрерывным увеличением скорости (течение Прандтля-Майера). Кроме этого рассматриваются математические модели, которые в одномерной постановке позволяют рассчитывать основные параметры пространственных течений в каналах. Наряду с изложением теоретических вопросов, приводится описание лабораторных работ, выполнение которых позволяет студентам закрепить теоретические знания на практике.

Теоретическая часть представлена в пособии с учетом особенностей подготовки специалистов по направлению 652200. Подробное изложение теоретических вопросов в пособии позволяет использовать его студентами как при подготовке к проведению лабораторных работ, так и к сдаче зачета по дисциплине "Механика жидкости и газа".

При написании учебного пособия учтен многолетний опыт проведения лабораторных работ на кафедре теории воздушно-реактивных двигателей МАИ. В частности использованы методические разработки профессоров этой кафедры В.В.Полякова, О.С.Сергеля и А.А.Степчкова.

Автор выражает свою признательность профессору кафедры теории воздушно-реактивных двигателей МАИ И.А.Лепешинскому за ряд ценных замечаний, учтенных при работе над пособием.

Течение вязкой жидкости в канале с местными гидравлическими сопротивлениями

Изложение теории

Течения в каналах являются пространственными течениями и для определения всех их параметров необходимо решать систему дифференциальных уравнений в частных производных. Но для расчета изменения по длине канала давления и средней по сечению канала скорости можно использовать математическую модель, полученную для элементарной струйки, т.е. модель одномерного течения. Для того чтобы применить уравнения элементарной струйки к потокам реальной жидкости в каналах, необходимо учесть в этих уравнениях отличие кинетической энергии, рассчитанной по среднемассовой скорости от истинной кинетической энергии неравномерного потока. Это делается с помощью коэффициента Кориолиса a, равного отношению действительной кинетической энергии потока с неравномерным полем скоростей к кинетической энергии потока с тем же расходом, но имеющего равномерное поле скоростей в том же сечении канала. Значение коэффициента Кориолиса зависит от режима течения жидкости (числа Рейнольдса); для ламинарного режима a = 2, для турбулентного a = 1,1 [5].

С учетом изложенного при стационарном течении вязкой несжимаемой (r = const) жидкости в канале переменного сечения среднемассовая скорость и давление жидкости в любом сечении канала могут быть найдены из решения системы двух уравнений – уравнения неразрывности и уравнения энергии в механической форме (уравнения Бернулли), записанных для двух сечений канала – 1 и 2:

F₁W₁ = F₂W₂ (1.1)

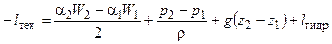(1.2)

В этих уравнениях: F – площадь поперечного сечения канала, W – среднемассовая скорость жидкости, r - ее плотность, p – давление, z – расстояние центра сечения канала от нивелирной плоскости, для которой z = 0, g – ускорение свободного падения, l_тех – техническая работа, l_гидр – работа, затраченная жидкостью на преодоление гидравлических сопротивлений, a - коэффициент Кориолиса.

Первый член правой части уравнения (1.2) описывает изменение кинетической энергии жидкости, второй – изменение потенциальной энергии давления и третий – изменение потенциальной энергии положения. В соответствии с уравнением Бернулли (1.2) техническая работа l_тех, подведенная к жидкости, идет на изменение ее кинетической энергии W²/2, потенциальной энергии давления р/r [совершение работы проталкивания (р₂-р₁)/r], потенциальной энергии положения gz и совершение работы по преодолению гидравлических сопротивлений l_гидр.

Последний член уравнения (1.2) учитывает гидравлические потери – уменьшение механической энергии жидкости вследствие трения о твердые поверхности и внутри жидкости. Гидравлические потери подразделяются на потери на трение и местные потери. Потери на трение связаны с движением вязкой жидкости вдоль твердых поверхностей, а местные потери – с образованием вихревых зон, возникающих при повороте потока, изменении площади канала и т.п.

Местные потери рассчитываются по формуле Вейсбаха [4]

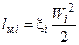(1.3)

Здесь: W_i – скорость в i-ом сечении канала, x_i – коэффициент местного сопротивления.

Потери на трение в канале круглого сечения длиной l и диаметром d определяются по формуле Дарси-Вейсбаха [4]

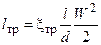(1.4)

В этой формуле: x_тр – коэффициент трения, W – средняя скорость жидкости на рассматриваемом участке канала (на его длине l).

Если поперечное сечение канала не является кругом, то в формулу (1.4) вместо диаметра d необходимо подставлять гидравлический диаметр d_г[4]:

.

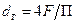Здесь: F – площадь поперечного сечения канала, П – его периметр.

Коэффициент трения зависит от числа Рейнольдса (режима течения) и относительной шероховатости стенок трубы:

x_тр = f(Re, D/r)

Здесь: Re – число Рейнольдса, D - средняя высота гребешков шероховатости, r – радиус (гидравлический радиус) канала.

Число Рейнольдса рассчитывается по формуле:

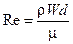
в которой: r, W и m - плотность, скорость и динамический коэффициент вязкости, d – диаметр (гидравлический диаметр) канала.

Для ламинарного режима течения жидкости в трубе (Re < 2300) [1, 4]

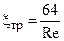
В этом случае

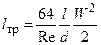~ W,

т.е. при ламинарном течении потери на трение пропорциональны скорости течения в первой степени.

При турбулентном режиме течения в трубе с гидравлически гладкой поверхностью стенок коэффициент трения рассчитывается по формуле Блазиуса [1, 4]

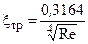2300 < Re < 10⁵

или по формуле Конакова [4]

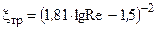Re > 10⁵

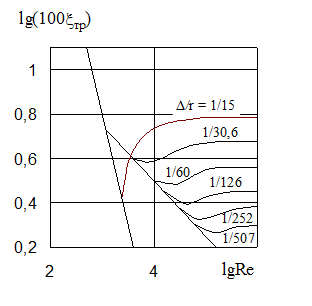
При больших значениях числа Рейнольдса (Re > 10⁵) коэффициент трения слабо зависит от Re; в этом случае потери на трение пропорциональны квадрату скорости жидкости и определяются только величиной относительной шероховатости стенок канала (рис. 1.1).

Из уравнения (1.1) следует, что при течении несжимаемой жидкости по каналу с постоянной площадью поперечного сечения (F₁ = F₂) W₁ = W₂, т.е. в этом случае скорость по всей длине канала остается постоянной: W = const. Если режим течения в канале не меняется, то a₁ = a₂ и первый член в правой части уравнения (1.2) обращается в нуль.

При течении несжимаемой жидкости по горизонтальному каналу (z₁=z₂) и отсутствии технической работы между рассматриваемыми сечениями (l_тех=0) уравнение (1.2) принимает вид:

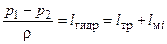[Дж/кг] (1.5)

В этом случае гидравлические потери на участке канала равны по абсолютной величине работе проталкивания или изменению потенциальной энергии давления на этом участке, т.е гидравлические сопротивления преодолеваются несжимаемой жидкостью за счет уменьшения потенциальной энергии давления этой жидкости при неизменном значении ее кинетической энергии.

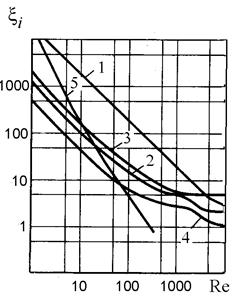
Местные потери определяются по формуле (1.3). При этом необходимо знать коэффициент местного сопротивления x_i. В первом приближении для типовых элементов трубопроводов (крана, фильтра и т.п.) значение этого коэффициента может быть определено по справочнику [3]. Зависимость коэффициента местного сопротивления некоторых элементов трубопроводов от числа Рейнольдса приведена на рис. 1.2.

В том случае, если местное сопротивление не является типовым или необходимо знать величину потерь с большей точностью, значение коэффициента местного сопротивления можно определить экспериментально. При этом используется уравнение (1.5), которое с учетом (1.4) принимает вид:

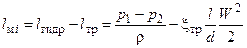[Дж/кг] (1.6)

В соответствии с формулой (1.3)

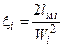(1.7)

Для того чтобы определить местные потери на каком-либо элементе трубопровода необходимо измерить разность давлений в двух сечениях трубопровода (перед и за местным сопротивлением) и скорость жидкости в трубопроводе. Вычитая из суммарных гидравлических потерь потери на трение на прямолинейном участке трубопровода, можно по формуле (1.6) определить l_мi.

Наряду с коэффициентом местных потерь для количественной оценки этих потерь в трубопроводах используют эквивалентную длину трубопровода l_экв. Это длина трубопровода, потери на трение по длине которого при той же скорости и диаметре равны потерям на местном сопротивлении, т.е.

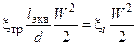
Отсюда

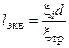
1.2. Лабораторная работа "Определение гидравлического сопротивления крана"

Цели работы - определение местного гидравлического сопротивления крана, коэффициента сопротивления крана, эквивалентной длины трубопровода, зависимости этих величин от числа Рейнольдса.

Косые скачки уплотнения

Изложение теории

Картина обтекания одного и того же тела дозвуковым и сверхзвуковым потоками качественно различна. При обтекании тела дозвуковым потоком элементарные волны давления, возникающие при взаимодействии потока с телом, распространяются во все стороны со скоростью звука. Эти волны уже на достаточном расстоянии искривляют линии тока, подготавливая поток для плавного обтекания тела. При обтекании затупленного тела сверхзвуковым потоком элементарные волны давления не могут распространяться против сверхзвукового потока и "подготавливать" его для плавного обтекания. Поэтому сверхзвуковой поток "натыкается" на препятствие так, что на некотором расстоянии от тела образуется скачок уплотнения, на котором ударно тормозится сверхзвуковой поток. Скачок уплотнения представляет собой сильную волну сжатия малой толщины (порядка длины свободного пробега молекул), в которой все параметры газа изменяются на конечную величину. Наличие скачкообразного изменения параметров газа на участке, имеющем малую протяженность (порядка длины свободного пробега молекул) указывает на то, что здесь имеет место внутренний молекулярный перенос, связанный с переходом кинетической энергии упорядоченного течения газа в кинетическую энергию беспорядочного теплового движения молекул. В результате этого происходит разогрев газа при прохождении его из невозмущенной области перед фронтом скачка уплотнения в область возмущенного движения за фронтом скачка уплотнения. Повышение средней квадратичной скорости движения молекул вызывает также возрастание давления и плотности невозмущенного газа при прохождении его через фронт скачка уплотнения.

При составлении математической модели течения газа через скачок уплотнения принимается, что газ является идеальным, а скачок уплотнения в связи с его малой толщиной рассматривается как геометрическая поверхность. Поверхность скачка является поверхностью сильного разрыва параметров газа – на ней все параметры газа и их производные терпят разрыв. В случае скачка уплотнения поверхность разрыва является нормальной, так как она перпендикулярна вектору скорости или его нормальной составляющей.

Скачки уплотнения могут быть прямыми или косыми. Прямыми скачками уплотнения называются скачки, фронт которых перпендикулярен вектору скорости набегающего потока. Косыми скачками уплотнения называются скачки, фронт которых составляет с вектором скорости набегающего потока угол a, отличный от прямого. Этот угол может меняться от угла характеристики a₀ до 90°. Косые скачки уплотнения возникают при повороте сверхзвукового потока, например при сверхзвуковом обтекании клина.

На рис. 2.1 показана фотография обтекания клина, полученная теневым методом. Ось клина совпадает с направлением вектора скорости невозмущенного потока. В этом случае на вершине клина образуются два косых скачка уплотнения, симметричных относительно оси симметрии клина.

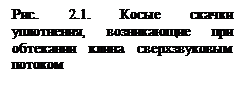
Задача обтекания клина сверхзвуковым потоком сводится к задаче обтекания этим потоком внутреннего тупого угла (180°- w), изображенного на рис. 2.2. На косом скачке уплотнения сверхзвуковой поток поворачивает на угол w: если первоначально газ двигался параллельно поверхности АВ, то после поворота он будет двигаться параллельно поверхности ВС. Параметры потока перед скачком уплотнения обозначим индексом н, а за скачком – индексом 1. До скачка уплотнения вектор скорости 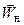составляет с фронтом скачка угол a, а за скачком вектор скорости 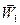составляет с фронтом скачка угол b. Из рисунка следует, что

a=w+b (2.1)

Разложим векторы скорости газа до скачка 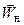и за скачком 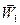на составляющие, нормальные и тангенциальные к фронту скачка: W_нn, W_нt и W_1n, W_1t.

При пересечении косого скачка уплотнения газом нормальная составляющая его вектора скорости скачкообразно уменьшается на конечную величину (W_1n<W_нn), а тангенциальная оcтается неизменной (W_1t=W_нt=W_t). Для того, чтобы доказать это рассмотрим рис. 2.3, на котором изображен косой скачок уплотнения и контрольный объем н-1-1-н. Боковые поверхности н-1 этого объема перпендикулярны, а торцевые поверхности н-н и 1-1 параллельны фронту скачка. При этом площади поверхностей н-н и 1-1 равны: F_н = F₁. Так как давления на обеих боковых поверхностях н-1 одинаковы, то из уравнения количества движения, записанного в проекции на направление фронта скачка следует, что тангенциальная составляющая скорости W_t остается неизменной, откуда и вытекает условие W_1t=W_нt=W_t. Уравнение количества движения в проекции на нормаль к скачку с учетом равенства площадей F_н и F₁ (F_н=F₁=F)записывается следующим образом

F(p_н – р₁) = G(W_1n – W_нn)

В этом уравнении G – расход газа через поверхность н-н (или 1-1). Так как р₁> p_н, то W_1n< W_нn.

В связи с тем, что при пересечении косого скачка нормальная составляющая скорости газа W_n уменьшается, а тангенциальная составляющая W_t остается неизменной, косой скачок уплотнения можно представить как прямой скачок для нормальной составляющей скорости, сносимый вдоль фронта косого скачка со скоростью W_t.

В теории косых скачков уплотнения вводятся дополнительно три параметра течения: температура частичного торможения Т_n, условная критическая скорость звука a_крn и приведенная скорость l_n.

Температура частичного торможения - температура, которую принимает газ при энергетически изолированном погашении до нуля только нормальной составляющей скорости. Эта температура рассчитывается по формуле:

Т_n^*=Т+W_n²/2c_p

в которой: T - статическая температура газа, c_p – удельная теплоемкость газа при постоянном давлении.

Условная критическая скорость звука – критическая скорость звука, рассчитанная по формуле

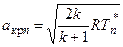
Приведенная скорость l_n – отношение нормальной составляющей скорости к условной критической скорости звука:

l_n=W_n/a_кpn

Получим формулы, связывающие параметры газа перед и за косым скачком уплотнения.

Течение в косом скачке уплотнения, также как и течение в прямом скачке уплотнения является энергетически изолированным (l_тех = 0 и q_н= 0) и поэтому из уравнения энергии в тепловой форме, записанного для элементарной струйки, пересекающей скачок (рис. 2.4), q_н - l_тех= i₁^* - i_н^* = с_р(Т₁^* - Т_н^*) следует i₁^* = i_н^* , Т₁^* = Т_н^* . Т.е. полная энергия газа, равная полной энтальпии (энтальпии торможения) газа, на косом скачке уплотнения не изменяется. Так как 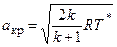и Т₁^* = Т_н^*, то а_кр1 = а_кр.н= а_кр.

Можно показать, что температура частичного торможения Т_n^*, также как и температура торможения Т^*, на косом скачке остается постоянной.

По определению Т_n^*=Т+W_n²/2c_p. Так как W² = W_n² +W_t², то

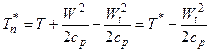
или для сечений н-н и 1-1 элементарной струйки, пересекающей скачок (рис. 2.4):

,

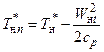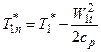
На косом скачке уплотнения Т₁^* = Т_н^* и W_1t = W_нt, следовательно Т_1n^* = Т_нn^*. Из этого равенства следует, что a_кр1n= a_кр.нn= a_крn.

Приведенные скорости l_нn и l_1n не являются нормальными составляющими приведенных скоростей l_ни l₁. Покажем это на примере приведенной скорости l_нn. Из рис. 2.2 следует, что W_нn = W_н×sina. Для того, чтобы в этом уравнении перейти к приведенным скоростям, необходимо левую часть разделить на a_кр.нn, а правую - на a_кр.н. Так как a_кр.нn ¹ a_кр.н, то l_нn¹l_н×sina. Таким же образом можно доказать, что l_1n¹l₁×sinb.

В отличие от приведенной скорости l_n число Маха М_n является нормальной составляющей М как перед, так и за скачком уплотнения

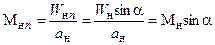(2.2а) 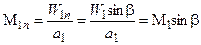(2.2б)

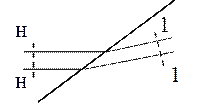
Так как косые скачки уплотнения являются прямыми скачками уплотнения для нормальных составляющих вектора скорости, то эти скачки можно рассчитывать по формулам, полученным для прямых скачков уплотнения с заменой l_ни l₁на l_нn и l_1n. Выполнив эту замену, получим следующие формулы, связывающие параметры течения за скачком с параметрами течения перед скачком:

- основное кинематическое соотношение

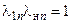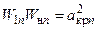или (2.3)

- уменьшение полного давления газа

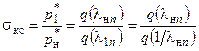(2.4)

- увеличение плотности газа

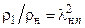(2.5)

- увеличение статического давления газа

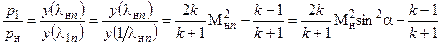(2.6)

- увеличение статической температуры

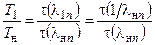(2.7)

Уравнение ударной адиабаты, состоящее из скалярных параметров, сохраняет ту же форму, что и для прямого скачка

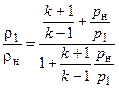
Часто при решении задач необходимо знать величину приведенной скорости за косым скачком уплотнения l₁. Связь между l₁ и l_нможно найти из треугольников скоростей за и перед скачком уплотнения (рис. 2.2):

W_1t = W₁ cosb = W_нt = W_н cosa

Отсюда

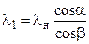
Из этих треугольников скоростей также можно получить уравнение, связывающее углы a, b и приведенную скорость l_нn. Разделив почленно W_нn = W_нttga на W_1n = W_1ttgb с учетом W_нt= W_1t, имеем:

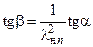(2.8)

Формулы (2.3)-(2.7) позволяют проводить как расчет, так и анализ изменения параметров газа при пересечении им косого скачка уплотнения.

Из формулы (2.3) следует, что за косым скачком уплотнения всегда l_1n < 1 и W_1n < a_крn, так как l_нn > 1 и W_нn > a_крn. Но скорость W₁ за косым скачком может быть как дозвуковой, так и сверхзвуковой. Так как при увеличении l значение газодинамической функции t(l) уменьшается, значение у(l) увеличивается и при l > 1 значение q(l) уменьшается, то t(l_нn)<t(l_1n), y(l_нn)>y(l_1n) и q(l_нn)<q(l_1n). В соответствии с формулами (2.4), (2.6) и (2.7) s_кс = р₁^*/ р_н^* < 1, p₁/p_н >1 и Т₁/Т_н >1. Из формулы (2.5) следует, что r₁/r_н >1. Это означает, что в косом скачке уплотнения (также как и в прямом, но в меньшей степени) полное давление уменьшается, а статическое давление и статическая температура увеличиваются. Качественное изменение параметров газа при пересечении им косого скачка уплотнения показано на рис. 2.2.

Приведенный формальный анализ изменения параметров газа при пересечении им скачка уплотнения полностью соответствует физической картине течения. Действительно, течение газа, пересекающего скачок уплотнения, является энергетически изолированным. Это означает, что полная энергия газа, равная полной энтальпии, остается постоянной. Полная энергия газа складывается из его тепловой энергии, потенциальной энергии давления и кинетической энергии (потенциальная энергия положения в случае газовых течений мала по сравнению с перечисленными видами энергии и ей можно пренебречь). Как было отмечено выше, при пересечении скачка уплотнения газом происходит увеличение его температуры и давления, что приводит к увеличению тепловой энергии и потенциальной энергии давления газа. В результате этого при постоянной полной энергии газа уменьшается кинетическая энергия и, соответственно, скорость газа. Уменьшение скорости газа при пересечении им скачка уплотнения следует и из уравнения обращения воздействий

,

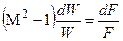в соответствии с которым при уменьшении площади сечения элементарной струйки сверхзвукового потока (рис. 2.4) скорость этого потока должна уменьшаться.

В соответствии с формулой (2.4) полное давление газа при пересечении им скачка уплотнения уменьшается. Это позволяет сделать вывод о том, что прохождение идеального газа сквозь скачок уплотнения не является изоэнтропическим процессом, а сопровождается необратимым переходом механической энергии в тепло.

На практике расчет косого скачка уплотнения сводится к определению параметров газа за скачком уплотнения по заданным значениям угла w, числа Маха М_н и известным параметрам газа перед скачком уплотнения с использованием формул (2.4)-(2.7).

Для того, чтобы воспользоваться этими формулами, необходимо знать приведенную скорость l_нn, которую можно определить по нормальной составляющей числа Маха перед скачком уплотнения 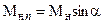. Связь между l_нn иМ_нn устанавливается формулой [1, 4]

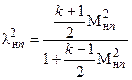(2.9)

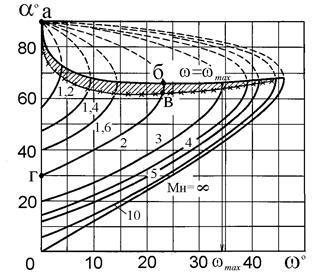При проведении расчетов значение l_нn удобнее находить по значению М_нn из таблиц газодинамических функций, не обращая внимания на индекс n. Заменив l_нn наМ_нn, мы заменили одно неизвестное на другое, так как для вычисления М_нn необходимо знать угол a. Этот угол можно найти по графикам a=f(М_н,w), построенным в результате решения системы уравнений (2.1), (2.2а), (2.8) и (2.9). Зависимость a=f(М_н,w) для газа с показателем адиабаты k = 1,4 (воздуха) графически представлена на рис. 2.5.

Точки пересечения кривых М_н= const с прямой w = 0 (точки г) соответствуют характеристикам сжатия, для которых 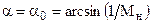. Участки кривых г-в соответствуют косым скачкам уплотнения, за которыми поток остается сверхзвуковым (М₁ > 1). Такие скачки называются слабыми косыми скачками. Участки кривых в-а соответствуют так называемым сильным косым скачкам, за которыми скорость потока становится дозвуковой (М₁ < 1). Опыт показывает, что в обычных условиях сильные косые скачки, соответствующие участкам кривых б-а, не реализуются, так как они являются неустойчивыми. Из рисунка видно, что прямая w = const пересекает кривые М_н = const в двух точках, т.е. одному значению w при заданном М_н могут соответствовать два значения угла a. Из приведенного выше следует, что из этих углов a необходимо выбирать меньшее значение, при котором реализуется устойчивый косой скачок уплотнения. Кроме этого из рис. 2.5 следует, что для заданного значения числа М_н существует максимальный угол отклонения потока в косом скачке уплотнения w_max. Если w > w_max, то поворот потока в косом скачке уплотнения не возможен и перед телом возникает отошедшая (отсоединенная) ударная волна, в которой угол a меняется от 90° до a₀.

2.2. Лабораторная работа "Теоретическое и экспериментальное исследование косых скачков уплотнения"

Цель работы - теоретическое и экспериментальное исследование изменения параметров газа на косом скачке уплотнения. После обработки экспериментальных данных и проведения теоретических расчетов должны быть получены зависимости a=f₁(w), s=f₂(a) и р₁/р_н=f₃(a), которые представляются в виде графиков, позволяющих сравнить результаты расчета и эксперимента.

Теоретические расчеты

В данной работе проводится сопоставление расчетных и экспериментальных зависимостей, полученных для постоянного числа Маха невозмущенного потока (М_н= const). Это означает, что при проведении эксперимента число Маха в рабочей части трубы должно быть постоянным по времени и расчеты должны проводиться для этого числа Маха. Но вследствие случайных факторов скорость потока в рабочей части аэродинамической трубы может незначительно меняться. Принимая это во внимание, расчеты выполняются для числа Маха невозмущенного потока М_н, которое является средним арифметическим между значениями чисел Маха М_нj, полученными в эксперименте (столбец № 13 табл. 2.1): .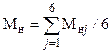

Теоретические расчеты удобнее проводить для заданных значений углов a. При проведении эксперимента на данном стенде угол косого скачка a меняется в диапазоне от 30° до 55°. Поэтому задаются следующие значения угла a - 30, 33, 36, 40, 43, 46, 50 и 55°, для которых при М_н, полученном в эксперименте, проводятся теоретические расчеты.

Для каждого заданного значения угла a проводятся следующие расчеты.

1. Определяется нормальная составляющая числа Маха М_н

M_нn = М_н sin a

2. По формуле (2.9) или по таблицам газодинамических функций по M_нnнаходитсяl_нn.

3. По таблицам газодинамических функций определяются значения газодинамических функций q(l_нn) и у(l_нn).

4. Из основного кинематического соотношения (2.3) находится приведенная скорость l_1n: l_1n = 1/l_нn.

5. По таблицам газодинамических функций определяются значения газодинамических функций q(l_1n) и у(l_1n).

6. Рассчитывается отношение давлений р₁/р_н: .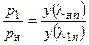

7. Вычисляется коэффициент потерь полного давления на косом скачке уплотнения

.

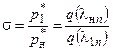8. Рассчитывается тангенс угла w

,

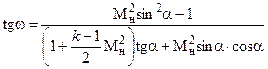по которому определяется угол w.

Результаты расчетов заносятся в табл. 2.2.

Таблица 2.2

№№ п/п	Мн	a	sina	sin2a	cosa	tga	tgw	w	Mнn	lнn
	-	град.	-	-	-	-	-	град.	-	-

Окончание табл. 2.2

q(lнn)	y(lнn)	l1n	q(l1n)	y(l1n)	p1/pн	s= p1*/pн*
-	-	-	-	-	-	-

Для удобства вычислений в табл. 2.2 записываются некоторые промежуточные данные расчетов: sina, sin²a, cosa, tg a.

По результатам обработки экспериментальных данных и теоретических расчетов строятся зависимости a=f₁(w), s=f₂(a) и р₁/р_н=f₃(a): сплошными кривыми изображаются теоретические зависимости, на которые точками наносятся данные эксперимента.

2.3. Вопросы для самостоятельной подготовки

1. Причины возникновения скачка уплотнения.

2. Дайте определение прямого и косого скачков уплотнения.

3. Поведение нормальной и тангенциальной составляющих вектора скорости на косом скачке уплотнения.

4. Температура частичного торможения Т_n*, условная критическая скорость звука a_крn, приведенная скорость l_n.

5. Основное кинематическое соотношение для косого скачка уплотнения.

6. Основное динамическое соотношение для скачка уплотнения.

7. Изменение параметров торможения газа на косом скачке уплотнения.

8. Изменение статических параметров газа на косом скачке уплотнения.

9. Объяснить зависимость a=f(М_н, w).

10. Измерение скорости сверхзвукового потока с помощью трубки Пито.

11. Какова цель лабораторной работы?

12. Опишите стенд, на котором проводится эксперимент.

13. Какова последовательность проведения эксперимента?

14. Последовательность обработки экспериментальных данных.

15. Последовательность проведения теоретических расчетов.

3. Сверхзвуковое течение с непрерывным увеличением скорости (течение Прандтля-Майера)

Изложение теории

Течение Прандтля-Майера реализуется при обтекании сверхзвуковым потоком внешнего тупого угла (180°+d). На рис. 3.1 приведена фотография обтекания клина, полученная теневым методом.

Ось клина составляет некоторый угол i с направлением вектора скорости невозмущенного потока. В этом случае на верхней поверхности клина образуется косой скачок уплотнения, а на нижней – центрированная волна разрежения, пересекая которую сверхзвуковой поток ускоряется.

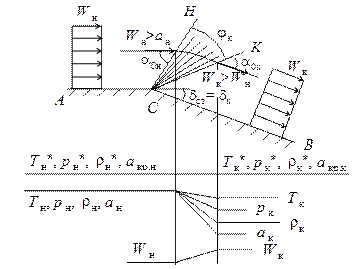
Рассмотрим обтекание сверхзвуковым потоком поверхности, образованной двумя полубесконечными пластинами, расположенными под углом d_ст друг к другу, т.е. образующими внешний тупой угол АВС, равный (180°+d_ст) (рис. 3.2).

Будем считать, что вдоль адиабатической стенки АС течет сверхзвуковой (l_н > 1) равномерный параллельный поток идеального газа. В этом случае течение вдоль стенки АС будет энергетически изолированным (Т^* = const) и изоинтропическим (р^* = const).

Вершина угла С является источником слабых возмущений, которые в виде бесчисленного множества прямолинейных характеристик разрежения располагаются в пределах угла НСК. Совокупность этих характеристик называется центрированной волной разрежения, так как все образующие ее характеристики исходят из одной точки. Первая характеристика СН располагается под углом 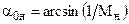к вектору скорости невозмущенного потока