Элементы современной физики атомов и молекул

§ 223. Атом водорода в квантовой механике

Решение задачи об энергетических уровнях электрона для атома водорода (а также систем:

иона гелия двукратно ионизован- ного лития и др.) сводится к зада- че о движении электрона в

ском поле ядра.

Потенциальная энергия взаимодей- ствия электрона с ядром, обладающим зарядом Ze (для атома водорода Z 1),

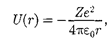(223.1)

где — расстояние между электроном и ядром.

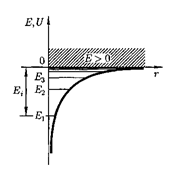
Графически функция U(r) изображе- на жирной кривой на рис. 305. 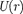с уменьшением 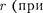приближении электрона к ядру) неограниченно убы- вает.

Состояние электрона в атоме водо- рода описывается волновой функци- ей 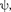удовлетворяющей стационарному уравнению Шредингера 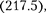учиты- вающему значение (223.1):

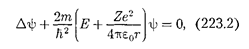
где т — масса электрона; Е — полная энергия электрона в атоме.

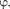Так как поле, в котором движется электрон, является центрально-сим- метричным, то для решения уравнения (223.2) обычно используют сфериче- скую систему координат: вда- ваясь в математическое решение этой задачи, ограничимся рассмотрением важнейших результатов, которые из него следуют, пояснив их физический

Энергия.В теории дифференци- альных уравнений доказывается, что

Рис. 305

уравнения типа (223.2) имеют решения, удовлетворяющие требованиям одно- значности, конечности и непрерывнос- ти волновой функции 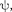только при собственных значениях энергии

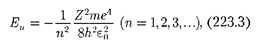
т.е. для дискретного набора отрица- тельных значений энергии.

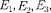Таким образом, как и в случае «по- тенциальной ямы» с бесконечно высо- кими «стенками» (см. § 220) и гармо- нического осциллятора (см. § 222), ре- шение уравнения Шредингера для ато- ма водорода приводит к появлению дискретных энергетических уровней. Возможные значения ... по- казаны на рис. 305 в виде горизонталь- ных прямых.

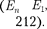Самый нижний уровень 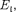отвеча- ющий минимальной возможной энер- гии, — основной, все остальные >

п= 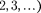— возбужденные (см. §

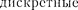При Е < 0 движение электрона явля- ется связанным — он находится внут- ри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа п энер- гетические уровни располагаются тес- нее и при п = оо 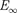= 0. При Е > 0 дви- жение электрона является свободным; область непрерывного спектра Е > 0 (заштрихована на рис. 305) соответ- ствует ионизованному атому. Энергия ионизации атома водорода равна

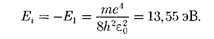Выражение (223.3) совпадает с фор- мулой (212.3), полученной Бором для энергии атома водорода. Однако если Бору пришлось вводить дополнитель- ные гипотезы (постулаты), то в кванто- вой механике значения

энергии, являясь следствием те- ории, вытекают непосредственно из ре- шения уравнения Шредингера.

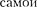
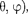
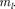2. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (223.2) удовлетворяют собственные функции 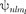(г, оп- ределяемые тремя квантовыми числа- ми: главным п, орбитальным 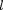и магнит- ным

Главное квантовое число п, соглас- но (223.3), определяет энергетические уровни электрона в атоме и может при- нимать любые целочисленные значе- ния, начиная с единицы:

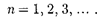
Из решения уравнения Шредингера вытекает, что момент импульса (меха- нический орбитальный момент) элект- ронаквантуется, е.неможетбытьпро- извольным, а принимает дискретные значения, определяемые по формуле

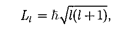(223.4)

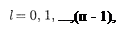где 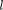— орбитальное квантовое чис- ло, которое при заданном п принимает значения

(223.5)

т.е. всего п значений, и определяет мо- мент импульса электрона в атоме.

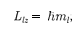Из решения уравнений Шрединге- ра следует также, что вектор 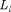момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция 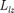на направле- ние z внешнего магнитного поля при- нимает квантованные значения, крат- ные

(223.6)

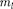где ~ магнитное квантовое число,которое при заданном 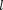может прини- мать значения

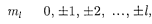= (223.7)

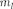т.е. всего 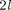+ 1 значений. Таким обра- зом, магнитное квантовое число оп- ределяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса элек- трона в атоме может иметь в простран- стве 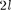+ 1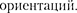

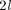
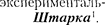Наличие квантового числа т, долж- но привести в магнитном поле к рас- щеплению уровня с главным кванто- вым числом п на + 1 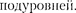Со- ответственно в спектре атома должно наблюдаться расщепление спектраль- ных линий. Действительно, расщепле- ние энергетических уровней в магнит- ном поле было обнаружено в 1896 г. голландским физиком (1865— 1945) и получило название эф- фекта 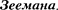Расщепление 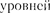энергии во внешнем электрическом поле, тоже доказанное

но, называется эффектом

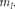Хотя энергия электрона (223.3) и зависит только от главного квантового числа п, но каждому собственному зна- чению 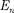(кроме 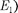соответствует не- сколько собственных функций 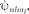от- личающихсязначениями/и Следо- вательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.

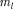Так как при данном п орбитальное квантовое число 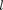может изменяться от О до п — 1 [см. (223.5)], а каждому зна- чению 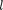соответствует 2/+ 1 различных значений (223.7), то число различ- ных состояний, соответствующих дан- ному п, равно

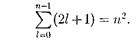(223.8)

Квантовые числа и их значения яв- ляются следствием решений уравнений

И. Штарк (1874 — 1957) — физик.

и условий однозначности, непрерывности и конечности, налагае- мых па волновую функцию 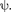Кроме того, так как при движении электрона в атоме существенны волновые свой- ства электрона, то квантовая механика вообще отказывается от классического представления об электронных орби- тах. Согласно механике, каж- дому энергетическому состоянию соот- ветствует волновая функция, квадрат модуля которой определяет вероят- ность обнаружения электрона в едини- це объема.

Вероятность обнаружения электро- на в различных частях атома неодина- кова. Электрон при своем движении как бы «размазан» по всему объему, обра- зуя электронное облако, плотность (гу- стота) которого характеризует вероят- ность нахождения электрона в различ- ных точках объема атома. Квантовые числа п и 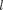характеризуют размер форму электронного облака, а

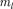вое число ~ ориентацию электрон- ногооблакавпространстве.

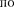В атомной физике, аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числа- ми 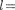0, называют s-состоянием (элек- трон в этом состоянии называют s-элек-

— —

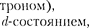
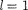
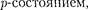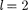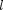= 3 — /-состоянием и т. д. Значение главного квантового чис- ла указывается перед условным обозна- чением орбитального квантового чис- ла. Например, электроны в состояниях с п 2 и 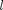0 и 1 обозначаются соответ- ственно символами 2s 2р.

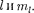
На рис. 306 для примера приведено распределение электронной плотности (формы электронного облака) для состо- яний атома водорода при п= 1 п = 2, определяемое 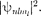Как видно из ри- сунка, оно зависит от п, Так, при 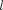0 электронная плотность отлична от

нуля в центре и не зависит от направ- ления (сферически-симметрична), а для остальных состояний в центре рав- на нулю и зависит от направления.

3. Спектр.Квантовые числа /, п позволяют более полно описать спектр испускания (поглощения) атома водо- рода, полученный в теории Бора (см. рис. 297).

В квантовой механике вводятся пра- вила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и по- глощением света. Теоретически доказа- но и экспериментально подтверждено, что для излучения электро- на, движущегося в центрально-симмет- ричном поле ядра, могут осуществлять- ся только такие переходы, для которых:

1) изменение орбитального кванто- вого числа Д 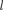удовлетворяет условию

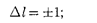(223.9)

2) 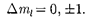изменение магнитного квантово- го числа 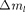удовлетворяет условию

В оптических спектрах указанные правила отбора в основном выполняют- ся. Однако в принципе могут наблю- даться и слабые «запрещенные» линии, например возникающие при переходах с 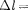2. Появление этих линий объяс- няется тем, что строгая теория, запрещая дипольные переходы, разрешает перехо- ды, соответствующие излучению более сложных систем зарядов, например квадруполей. Вероятность же квадру- переходов (переходы с 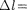2)

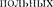во много раз меньше вероятности ди- польиых переходов, поэтому «запре- щенные» линии и являются слабыми.

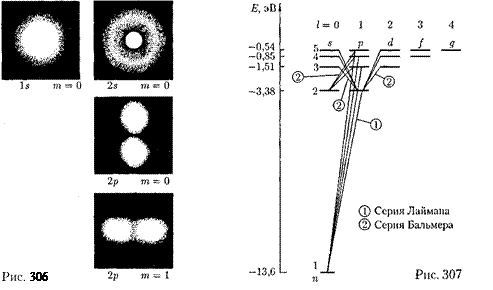
Учитывая число возможных состо- яний, соответствующих данному п, и правило отбора (223.9), рассмотрим спектральные линии атома водорода (рис. 307). Серии Лаймана соответству- ют переходы

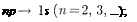
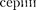Бальмера —

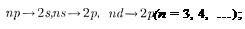
и т. д.

Переход электрона из основного со- стояния в возбужденное обусловлен увеличением энергии атома и может происходить только при сообщении атому энергии извне, например за счет поглощения атомом фотона. Так как поглощающий атом находится обычно в основном состоянии, то спектр атома водорода должен состоять из линий, соответствующих переходам 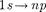(п= 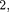3, ...), что находится в полном согласии с опытом.

§ 224. 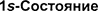электрона в атоме водорода

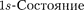электрона в атоме во- дорода является сферически-симмет- ричным. Волновая функция 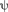электро- на в этом состоянии определяется толь- ко расстоянием электрона от ядра, т. е.

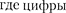
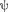
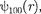в индексе соот- ветственно указывают, что п — 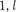= 0 и

— 0. Уравнению Шредингера для электрона в атоме водоро-

да удовлетворяет функция вида

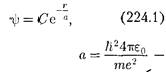= (224.1)

где, как можно показать,

величина, совпадающая с первым оо- ровским радиусом а [см. (212.2)] для атома водорода; С — некоторая посто- янная, определяемая из условия норми- ровки вероятностей (216.3).

Благодаря сферической симметрии 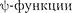вероятность обнаружения электрона на расстоянии одинакова по всем направлениям. Поэтому эле- мент объема dV, отвечающий одинако- вой плотности вероятности, обычно представляют в виде объема сферичес- кого слоя радиусом и толщиной dr: dV = 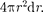Тогда, согласно условию

нормировки вероятностей 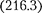с уче- том (224.1),

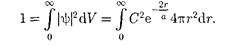После интегрирования получим

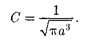(224.2)

Подставив выражение (224.2) в фор- мулу (224.1), определим нормирован- ную волновую функцию, отвечающую

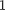«-состоянию электрона в атоме водо- рода:

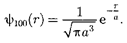(224.3)

Вероятность обнаружить электрон в элементе объема [см. (216.2)] равна

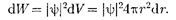
Подставив в эту формулу волновую функцию (224.3), получим плотность вероятности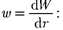

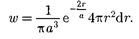
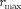Вычислим те расстояния от ядра, на которых электрон может быть обна- ружен с наибольшей вероятностью.

Исследуя выражение — па максимум,

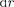
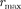получим, что = а. Следовательно, электрон может быть обнаружен с наи- большей вероятностью на расстояниях, равных боровскому радиусу, т. е. имеет- ся равная и наибольшая вероятность обнаружения электрона во всех точках, расположенных на сферах радиуса а с центром в ядре атома.

Казалось бы, квантово-механиче- 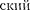расчет дает полное согласие с тео- рией Бора. Однако, согласно квантовой механике, плотность вероятности лишь

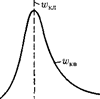Рис. 308

при = а достигает максимума, остава- ясь отличной от нуля во всем простран- стве (рис. 308). Таким образом, в основ- ном состоянии атома водорода наибо- лее вероятным расстоянием от электро- на до ядра является расстояние, равное боровскому радиусу. В этом заключа- ется 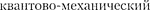смысл бо-

ровского радиуса.

§225.Спинэлектрона.

Спиновое квантовое число

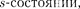
и В.Герлах, проводя пря- мые измерения магнитных моментов (см. § 131), обнаружили в 1922 г., что узкий пучок атомов водорода, заведо- мо находящихся в в не- однородном магнитном поле расщепля- ется на два пучка. В этом состоянии мо- мент импульса электрона равен нулю [см. (223.4)]. Магнитный момент ато- ма, связанный с орбитальным движени- ем электрона, пропорционален механи- ческому моменту [см. 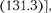поэтому он равен нулю и магнитное поле не дол- жно оказывать влияния на движение атомов водорода в основном состоянии, т.е. расщепления быть не должно. Од- нако в дальнейшем при применении спектральных приборов с большой раз- решающей способностью было доказа- но, что спектральные атома во- дорода обнаруживают тонкую структу- ру (являютсядублетами) даже в отсут- ствие магнитного поля.

Для объяснения тонкой структуры спектральных линий, а также ряда дру- гих трудностей в атомной физике аме- риканские физики Д. (1900 — 1974) и С. Гаудсмит - 1979) пред- положили, что электрон обладает соб- ственным неуничтожимым механиче- ским моментом импульса, не связан- ным с движением электрона в простран- стве, — спином 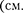§ 131).

Спин электрона (и всех других мик- рочастиц) — квантовая величина, у нее нет классического аналога; это внутрен- нее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается соб- ственный механический момент им- пульса (спин) 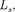то ему соответствует собственный магнитный момент Согласно общим выводам квантовой механики, спин квантуется по закону

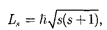
где s — спиновое квантовое число.

По аналогии с орбитальным момен- том импульса, спина кван- туется так, что вектор может прини- мать 2 s + 1 Так как в опы- тах Штерна и Герлаха наблюдались только две ориентации, то 2s + 1 2, откуда s 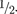Проекция спина на на- правление внешнего магнитного поля, являясь квантованной величиной, оп- ределяется выражением, аналогичным (223.6):

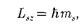
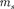
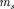где — магнитное спиновое кванто- вое число; оно может иметь только два значения: =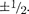

Таким образом, опытные данные привели к необходимости характеризо- вать электроны (и микрочастицы вооб- ще) добавочной внутренней степенью свободы. Поэтому для полного описа-

ния состояния электрона в атоме необ- ходимо наряду с главным 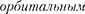и магнитным квантовыми числами за- давать еще магнитное спиновое кван- товоечисло.

§226.Принципнеразличимости тождественныхчастиц.

Фермионы и бозоны

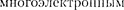Если перейти от рассмотрения дви- жения одной микрочастицы (одного электрона) к сис-

темам, то проявляются особые свой- ства, не имеющие аналога в классиче- ской физике. Пусть

ческая система состоит из одинаковых частиц, например электронов. Все элек- троны имеют одинаковые физические свойства — массу, электрический заряд, спин и другие внутренние характерис- тики (например, числа). кие частицы называют тождествен- ными.

Необычные свойства системы оди- наковых тождественных частиц прояв- ляются в фундаментальном принципе квантовой механики — принципе не- различимости тождественных час- согласно которому невозможно экспериментально различить тожде-

ственные частицы.

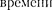В классической механике даже оди- наковые частицы можно различить по положению в пространстве и импуль- сам. Если частицы в какой-то момент времени пронумеровать, то в следую- щие моменты можно просле- дить за траекторией любой из них. Классические частицы, таким образом,

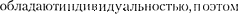у классическая механика систем из оди- наковых частиц принципиально не от- личается от классической механики систем из различных частиц.

В квантовой механике положение иное. Из соотношения неопределенно- стей вытекает, что для микрочастиц во- обще неприменимо понятие траекто- рии; состояние микрочастицы описыва- ется волновой функцией, позволяющей вычислять лишь вероятность 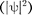на- хождения микрочастицы в окрестнос- тях той или иной точки пространства. Если же волновые функции двух тож- дественных частиц в пространстве пе- рекрываются, то разговор о том, какая частица находится в данной области, вообще лишен смысла: можно лишь го- ворить о вероятности нахождения в данной области одной из тождествен- ных частиц.

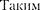образом, в квантовой механи- ке тождественные частицы полностью теряют свою индивидуальность и ста- новятся неразличимыми. Следует под- черкнуть, что принцип неразличимос- ти тождественных частиц не является просто следствием вероятностной ин- терпретации волновой функции, а вво- дится в квантовую механику как новый принцип, который, как уже указывалось, является фундаментальным.

Принимая вовниманиефизический смысл величины 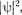принцип неразли- чимости тождественных частиц можно записать в виде

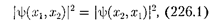
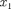
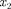где — соответственно совокуп- ность пространственных и спиновых координат первой и второй частиц. Из выражения (226.1) вытекает, что воз- можны два случая:

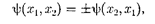
т.е. принцип неразличимости тожде- ственных частиц ведет определенному свойствусимметрииволновойфункции. Если при перемене частиц местами вол- новая функция не меняет знака, то она

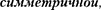называется если меня- ет— антисимметричной.

Изменение знака волновой функции не означает изменения состояния, так как физический смысл имеет лишь квадрат модуля волновой функции. В квантовой механике доказывается, что характер симметрии волновой функции не меняется со временем. Это же явля- ется доказательством

симметрии или антисимметрии — при- знак данного типа микрочастиц.

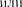
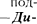Установлено, что симметрия ан- тисимметрия волновых функций опре- деляется спином частиц. В зависимос- ти от характера симметрии все элемен- тарные частицы и построенные из них системы (атомы, молекулы) делятся па два класса. Частицы с полуцелым спи- ном (например, электроны, протоны, нейтроны) описываютсяантисиммет- ричными волновыми функциями чиняются статистике Ферми

рака] эти частицы называются ферми- онами.

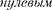
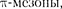
Частицы с или целочислен- ным спином (например, фо- тоны) описываются симметричными волновыми функциями

статистике Бозе эти частицы называются бозонами. Слож- ные частицы (например, атомные ядра), составленные из нечетного числа фер- мионов, фермионами (сум- марный спин — а из чет- ного — бозонами (суммарный спин це- лый).

Зависимость характера симметрии волновых функций системы тожде- ственных частиц от спина частиц тео- ретически обоснована швейцарским физиком В.Паули (1900-1958), что явилось еще одним доказательством того, что спин является фундамен- тальной характеристикой микрочас- тиц.

§ 227. Принцип Паули.