И конденсатора. Энергия электростатического поля

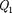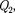1. Энергия системы неподвижных точечныхзарядов.Электростатиче- ские силы взаимодействия консерватив- ны (см. § 83); следовательно, система за- рядов обладает потенциальной энерги- ей. Найдем потенциальную энергию си- стемы двух неподвижных точечных за- рядов и находящихся на рассто- янии г друг от друга. Каждый из этих зарядов в поле другого обладает потен- циальной энергией [см. (84.2) и (84.5)]:

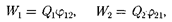
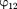
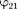
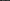
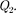где и соответственно потенци- алы, создаваемые зарядом 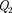в точке на- хождения заряда 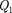и зарядом 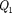в точ- ке нахождения заряда

Согласно (84.5),

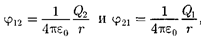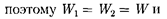
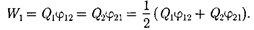Добавляя к системе из двух зарядов последовательнозаряды мож- но убедиться в том, что в случае п не- подвижных зарядов энергия взаимо- действия системы точечных зарядов равна

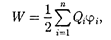
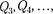(95.1)

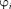
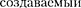
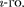где — потенциал, в точке, где находится заряд всеми за- рядами, кроме

2. Энергия заряженного уединен- ного проводника.Пусть имеется уеди- ненный проводник, заряд, емкость и по- тенциал которого соответственно рав- ны Q, С, ф. Увеличим заряд данного проводника на dQ. Для этого необходи- мо перенести заряд dQ из бесконечнос- ти па уединенный проводник, затратив на это работу

— =

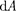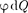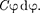
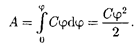Чтобы зарядить тело от нулевого потен- циала до ф, необходимо совершить ра- боту

(95.2)

Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот про- водник:

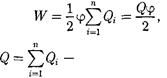Формулу (95.3) можно получить исходя и из того, что потенциал провод- ника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Полагая потенци- ал проводника равным ф, из формулы (95.1) найдем

где заряд проводника.

3. Энергия заряженного конденса- тора.Как всякий заряженный провод- ник, конденсатор обладает энергией, которая в соответствии с формулой (95.3) равна

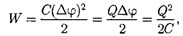(95)

где Q — заряд конденсатора; С — его емкость; 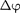— разность потенциалов между обкладками конденсатора.

Используя выражение (95.4), мож- но найти механическую (пондеромо- 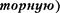силу, с которой пластины конденсатора притягивают друг друга. Предположим, что первоначальное расстояние х между пластинами уве- личиваем на 6х. При этом приложен- ная к пластине сила совершает работу 6А — 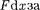счет уменьшения потенци- альной энергия системы: откуда

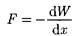(95.5)

Подставив в (95.4) выражение (94.3), получим

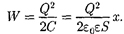(95.6)

Производядифференцирование при конкретном значении энергии [см. (95.5) и (95.6)], найдем искомую силу:

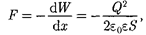
где знак «—» указывает, что сила F яв- ляется силой притяжения.

4.Энергия электростатического поля. Преобразуем формулу (95.4), вы- ражающую энергию плоского конден- сатора посредством зарядов и потенци- алов, воспользовавшись выражением для емкости плоского конденсатора

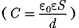и разности потенциалов между его обкладками 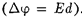Тогда

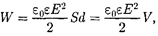(95.7)

где V = Sd — объем конденсатора.

Формула (95.7) показывает, что энергия конденсатора выражается через величину, характеризующую электро- статическое поле, — напряженность Е. Объемная плотность энергии элек- тростатического поля (энергия едини-

цы объема)

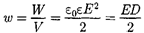(95.8)

Выражение (95.8) справедливо толь- кодля изотропного диэлектрика, для которого выполняется соотношение (88.2):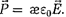

Формулы (95.4) и (95.7) соответ- ственно связывают энергию конденса- тора с зарядом на его обкладках и с на- пряженностью поля. Возникает, есте- ственно, вопрос о локализации энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос мол-сет дать только опыт. Электростатика изу- чает постоянные во времени поля непод- вижных зарядов, т. е. в ней поля и обус- ловившие их заряды неотделимы друг от друга, поэтому электростатика ответить на поставленные вопросы не может.

Дальнейшее развитие теории и экс- виде электромагнитных волн, - перимента показало, что 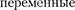во них переносить энергию. Это убеди- времени электрические и магнитные тельно подтверждает основное положе- поля могут существовать обособленно, ние теории независимо от возбудивших их зарядов, кализована в поле и носителем энергии и распространяться в пространстве в является поле.

Контрольные вопросы

• В чем заключается закон сохранения заряда? Приведите примеры проявления закона.

• Запишите, сформулируйте и объясните закон Кулона.

• Какие поля называют электростатическими?

• Что такое напряженность Е электростатического поля?

• Каково направление вектора напряженности Е? Единица напряженности в СИ.

• Что такое поток вектора Е? Единица его в СИ?

• Электрический диполь помещен внутрь замкнутой поверхности. Каков 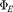сквозь эту поверхность?

• Пользуясь принципом суперпозиции, найдите в поле двух точечных зарядов Q и +2 Q,

находящихся на расстоянии /друг от друга, точку, где напряженность поля равна нулю.

• Чему равно отношение папряженностей электростатических полей в 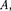лежащей на продолжении оси диполя, и в точке В, лежащей на перпендикуляре, проходящем че- рез середину О оси этого диполя, если А — ОВ?

• В чем заключается физический смысл теоремы Гаусса для электростатического поля в вакууме?

• Что такое линейная, поверхностная и объемная плотности зарядов?

• Как показать, что электростатическое поле является потенциальным?

• Что называется циркуляцией вектора напряженности?

• Дайте определения потенциала дайной точки электростатического поля и разности по- тенциалов двух точек поля. Каковы их единицы?

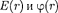• Приведите графики зависимостей для равномерно заряженной сферической поверхности. Дайте их объяснение и обоснование.

• Какова связь между напряженностью и потенциалом электростатического поля? Выве- дите ее и объясните. Каков физический смысл этих понятий?

• Чему равна работа по перемещению заряда вдоль эквипотенциальной поверхности?

• Что такое поляризованность?

• Что показывает диэлектрическая проницаемость среды?

• Выведите связь между диэлектрическими восприимчивостью вещества и проницаемо- стью среды.

• В чем различие поляризации диэлектриков с полярными и неполярными молекулами?

• Определите, чему равна диэлектрическая проницаемость при построении рис. 137.

• Как определяется вектор электрического смещения? Что он характеризует?

• Сформулируйте теорему Гаусса для электростатического поля в диэлектрике.

• Выведите и прокомментируйте условия для векторов Е и D на границе раздела двух диэлектрических сред.

• Каковы напряженность и потенциал поля, а также распределение зарядов внутри и на поверхности заряженного проводника?

• На чем основана электростатическая защита?

• Три одинаковых конденсатора один раз соединены последовательно, другой — парал- лельно. Во сколько раз и когда емкость батареи будет больше?

• Может ли электростатика ответить на вопрос: где локализована энергия и что является ее носителем — заряды или поле? Почему?

Выведите формулы для энергии заряженного конденсатора, выражая ее через заряд па обкладках конденсатора и через напряженность поля.

ЗАДАЧИ

11.1. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0,8 г/см3. Какова должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и керосине был один и тот же? Диэлектрическая прони- цаемость керосина 2. [1,6 г/см3]

11.2. На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью ст = 1,5 пКл/см2 расположена круглая пластинка. Плоскость пластинки составляет с линиями напряженности угол а = 45°. Определите поток вектора напряженности через эту пластинку, если ее радиус 10 см. 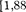кВ • м]

11.3.Кольцо радиусом г= 10 см из тонкой проволоки равномерно заряжено с линейной плотностью т = 10 нКл/м. Определите напряженность поля на оси, проходящей через центр кольца в точке А, удаленной на расстояние о = 20 см от центра кольца. [ 1 кВ/м]

11.4. 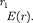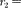Шар радиусом R = 10 см заряжен равномерно с объемной плотностью р = 5 нКл/м3. Определите напряженность электростатического поля: 1) па расстоянии 2 см от центра шара; 2) на расстоянии 12 см от центра шара. Постройте зависимость [1) 3,77 В/м; 2) 13,1 В/м]

11.5. Электростатическое поле создается положительно заряженной бесконечной ни- тью с постоянной линейной плотностью т = 1 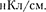Какую скорость приобретет элект- рон, приблизившись под действием поля к нити вдоль линии напряженности с расстояния

= 2,5 см до = 1,5 см? [18 Мм/с]

11.6. Электростатическое поле создастся сферой радиусом R = 4 см, равномерно заря- женной с поверхностной плотностью ст = 1 пКл/м2. Определите разность потенциалов между двумя точками поля, лежащими на расстояниях = 6 см и = 10 см. [1,2 В]

11.7. Определите линейную плотность бесконечно длинной заряженной нити, если ра- бота сил поля по перемещению заряда Q = 1 нКл с расстояния 10 см до = 5 см в направлении, перпендикулярном нити, равна 0,1 мДж. [8 мкКл/м]

11.8. Пространство между обкладками плоского конденсатора заполнено парафином 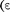= 2). Расстояние между пластинами d= 8,85 мм. Какую разность потенциалов необходи- мо подать на пластины, чтобы поверхностная плотность связанных зарядов на парафине составляла 0,05 нКл/см2? [500 В]

11.9. Свободные заряды с объемной плотностью р 10 нКл/м3 равномерно распределены по шару радиусом R = 5 см из однородного изотропного диэлектрика с диэлектрической проницаемостью = 6. Определите напряженности электростатического поля на расстоя- ниях = 2 см и = 10 см от центра шара. 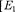= 1,25 В/м; 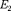= 23,5 В/м]

11.10. 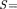Пространство между пластинами плоского конденсатора заполнено стеклом 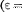7). Расстояние между пластинами d = 5 мм, разность потенциалов U= 500 В. Опреде- лите энергию поляризованной стеклянной пластины, если площадь 50 см2. [6,64 мкДж]

11.11. Плоский воздушный конденсатор емкостью 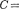10 пФ заряжен до разности по- тенциалов 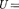1 кВ. После отключения конденсатора от источника напряжения расстоя- ние между пластинами конденсатора было увеличено в два раза. Определите: 1) разность потенциалов на обкладках конденсатора после их раздвижения; 2) работу внешних сил по раздвижению пластин. [1)2 кВ; 2) 5 мкДж]

11.12. Разность потенциалов между пластинами конденсатора U= 200 В. Площадь каж- дой пластины S — 100 см2, расстояние между пластинами d = 1 мм, пространство между ними заполнено парафином (е = 2). Определите силу притяжения пластин друг к другу. [3,54 мН]

Глава 12

§ 96. Электрический ток, сила и плотность тока

В электродинамике — разделе уче- ния об электричестве, в котором рас- сматриваются явления и процессы, обусловленные движением электриче- ских зарядов или макроскопических за- ряженных тел, — важнейшим понятием является понятие электрического тока. Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием прило- женного электрического поля 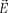свобод- ные электрические заряды перемеща- ются: положительные — по полю, отри- цательные — против поля (рис. 148, а), т.е. в проводнике возникает электри- ческий ток, называемый током прово-

димости.

Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заря- женного макроскопического тела (рис. 148, б), то возникает так называемый конвекционный ток.

Для возникновения и существова- ния электрического тока необходимо, с одной стороны, наличие свободных но- сителей тока — заряженных частиц,

способных перемещаться упорядочен- ие, а с другой — наличие электрическо- го поля, энергия которого, каким-то об- разом восполняясь, расходовалась бына их упорядоченное движение. Зана- правление тока условно принимают на- правление движения положительных зарядов.

Количественной мерой электричес- кого тока служит сила тока I —ска- лярная физическая величина, опреде- ляемая электрическим зарядом, прохо- дящим через поперечное сечение про- водника в единицу времени:

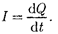Если сила тока иего направление не изменяются со временем, то такой ток называется постоянным. Для постоян- ного тока

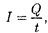где Q —электрический заряд, проходя- щий завремя t через поперечное сече- ние проводника. Единица силы тока — ампер (А) [см. Введение].

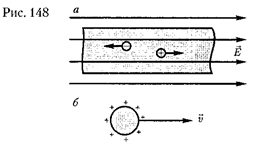Физическая величина, определяе- мая силой тока, проходящего через еди- ницу площади поперечного сечения проводника, перпендикулярного на- правлению тока, называется плотнос- тью тока:

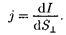Выразим силу и плотность тока че- рез скорость 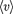упорядоченного движе- ния зарядов в проводнике. Если кон- центрация носителей тока равна п

177

каждый носитель имеет элементарный заряд е (что не обязательно для ионов), то за время dt через поперечное сече- ние S проводника переносится заряд dQ = ne(v)Sdt. Сила тока

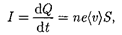
а плотность тока j — ne(v).

Плотность тока — вектор; направле- ние вектора j совпадает с направлени- ем упорядоченного движения положи- тельных зарядов:

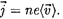(96.1)

Единица плотности тока — ампер на метр в квадрате (А/м2).

Сила тока сквозь произвольную по- верхность S определяется как поток

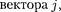т.е.

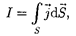(96.2)

где = 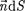(n — единичный вектор нормали к площадке 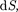составляющей с вектором j угол а).

§ 97. Сторонние силы. Электродвижущая сила и напряжение

Если в цепи на носители тока дей- ствуют только силы электростатическо- го поля, то происходит перемещение носителей (они предполагаются поло- жительными) от точек с большим по- тенциалом к точкам с меньшим потен- циалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Поэтому для существования постоян- ного тока необходимо наличие в цепи устройства, способного создавать и под- держивать разность потенциалов за

счет работы сил неэлектростатическо- го происхождения. Такие устройства называются источниками тока.

Силы неэлектростатическогопро- исхождения, действующие на заряды со стороны источников тока, называются сторонними.

Природа сторонних сил может быть различной. Например, в гальваничес- ких элементах они возникают за счет энергии химических реакций между электродами и электролитами; в гене- раторе — за счет механической энергии вращения ротора генератора и т. п. Роль источника тока в электрической цепи, образно говоря, такая же, как роль на- соса, который необходим для перека- чивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электрические за- ряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддер- живается разность потенциалов и в цепи течет постоянный электрический

Сторонние силы совершают работу по перемещению электрических заря- дов. Физическая величина, определяе- мая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой 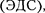дей- ствующей в цепи:

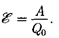(97.1)

Эта работа производится за счет энергии, затрачиваемой в источнике тока, поэтому величину 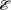можно также называть электродвижущей силой ис- точника тока, включенного в цепь. Ча- сто, вместо того чтобы сказать: «в цепи действуют сторонние силы», говорят:

«в цепи действует ЭДС», т.е. термин

«электродвижущая сила» употребляет-

ся как характеристика сторонних сил. ЭДС, как и потенциал, выражается в вольтах [ср. (84.9) и (97.1)].

Сторонняя сила 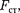действующая на заряд 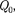может быть выражена как

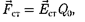
где 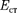— напряженность поля сторон- них сил.

Работа сторонних сил по перемеще- нию заряда 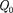на замкнутом участке цепи

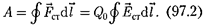
Разделив (97.2) на 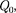получим вы- ражение для 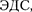действующей в цепи:

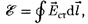т.е. ЭДС, действующая в замкнутой цепи, может быть определена как цир- куляция вектора напряженности поля сторонних сил. ЭДС, действующая на участке 1 — 2, равна

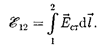(97.3)

На заряд 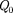помимо сторонних сил действуют также силы электростати- ческого поля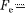 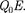Таким образом, результирующая сила, действующая в цепи на заряд 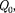равна

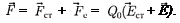
Работа, совершаемая результирую- щей силой над зарядом 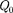на участке 1 — 2, равна

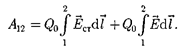
Используя выражения (97.3) и

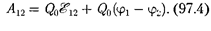(84.8), можем записать

Для замкнутой цепи работа электро- статических сил равна нулю (см. §83), поэтому в данном случае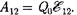

Напряжением U на участке 1 — 2 на- зывается физическая величина, опреде- ляемая работой, совершаемой суммар- ным полем электростатических (куло- новских) исторонних сил при переме- щении единичного положительного за- ряда на данном участке цепи. Таким образом, согласно (97.4),

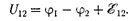Понятиенапряженияявляетсяобоб- щением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том слу- чае, если наэтом участке не действует ЭДС, т.е. сторонние силы отсутствуют.

§ 98. Закон Ома.

Сопротивлениепроводников

Немецкий физик Г. Ом (1787 —1854) экспериментально установил, что сила тока I, текущего по однородному метал- лическому проводнику (т.е. провод- нику, в котором не действуют сторон- ние силы), пропорциональна напряже- нию U на концах проводника

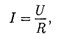(98.1)

где R — электрическое сопротивление проводника.

Уравнение (98.1) выражает закон Ома дляучастка цепи (не содержаще- го источника тока): сила тока в провод- нике прямо пропорциональна прило- женному напряжению и обратно про- порциональна сопротивлению провод- ника. Формула (98.1) позволяет уста- новить единицусопротивления ом(Ом): 1 Ом — сопротивление такого провод-

в котором при напряжении 1 В те- чет 1 А.

Величина

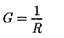называется электрической проводи- мостью проводника. Единицапроводи- мости — сименс(См): 1 См — прово- димость участка электрической цепи сопротивлением 1 Ом. Сопротивление проводников зависит от его размеров и формы, а также от материала, из кото- рого проводник изготовлен. Для одно- родного линейного проводника сопро- тивление R прямо пропорционально его длине 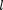и обратно пропорциональ- но площади его поперечного сечения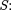

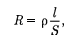(98.2)

где р — коэффициент пропорциональ- ности, характеризующий материал про- водника и называемый удельным элек- трическим сопротивлением.

Единица удельного электрического сопротивления — ом-метр(Ом*м).Наименьшим удельным сопротивлени- ем обладают серебро (1,6 • 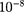Ом • м) и медь 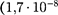Ом • м). На практике наряду с медными применяются алю- миниевые провода. Хотя алюминий и имеет большее, чем медь, удельное со- противление (2,6 • 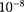Ом • м), но зато обладает меньшей плотностью по срав- нению с медью.

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (98.2) в закон Ома (98.1), получим

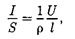(98.3)

где величина, обратная удельному со- противлению,

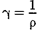
называется удельной электрической проводимостью вещества проводника. Ее единица — сименс на метр (См/м). Учитывая, что 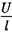• = Е — напряжен- ность электрического поля в проводни- ке, 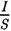= j — плотность тока, формулу

(98.3) можно записать в виде

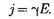(98.4)

Так как в изотропном проводнике носители тока в каждой точке движут- ся в направлении вектора Ё, то направ- ления j и Е совпадают. Поэтому фор- мулу (98.4) можно записать в виде

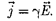(98.5)

Выражение (98.5) — закон Ома в дифференциальной форме, связыва- ющий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Опыт показывает, что в первом при- ближении изменение удельного сопро- тивления, а значит и сопротивления с температурой описывается линейным законом:

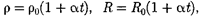
где р и р0, R и Ro — соответственно удельные сопротивления и сопротивле- ния проводника при t и О 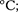— тем- пературный коэффициент сопро- тивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 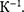Следовательно, температур- ная зависимость сопротивления может быть представлена в виде

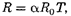(98.6)

где Т— термодинамическая температура.

Рис. 149

ся термисторами. Они позволяют из- мерять температуру с точностью до миллионных долей кельвин.

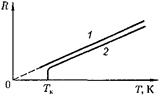Зависимость сопротивления от тем- пературы (98.6) представлена на рис. 149 (кривая 1). При низких температурах наблюдается отступление от этой зави- симости.

Впоследствии было обнаружено, что сопротивление многих металлов (на- пример, Al, Pb, Zn и др.) и их сплавов при очень низких температурах Тк (0,14 — 20 К), называемых критиче- скими, характерных для каждого веще- ства, скачкообразно уменьшается до нуля (кривая 2), т.е. металл становит- ся абсолютным проводником. Впервые это явление, названное сверхпроводи- мостью, обнаружено в 1911 г. Г. Камер- линг-Оннесом для ртути.

Явление сверхпроводимости объяс- няется на основе квантовой теории. Практическое использование сверхпро- водящих материалов (в обмотках сверх- проводящих магнитов, в системах па- мяти ЭВМ и др.) затруднено из-за их низких критических температур. В на- стоящее время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температуре выше 140 К.

На зависимости электрического со- противления металлов от температуры основано действие термометров со- противления, которые позволяют по градуированной взаимосвязи сопро- тивления от температуры измерять тем- пературу с точностью до 0,001 К. Тер- мометры сопротивления, в которых в качестве рабочего вещества использу- ются полупроводники, изготовленные по специальной технологии, называют-

§ 99. Работа и мощность тока.

Закон Джоуля—Ленца

Рассмотрим однородный провод- ник, к концам которого приложено на- пряжение U.

За время dt через сечение проводника переносится заряд dq — Idt. При этом силы электростатического поля и сторон- ние силы совершают работу [см. (84.6)]

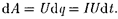(99.1)

Если сопротивление проводника R, то, используя закон Ома (98.1), полу- чим, что работа тока

Из (99.1) и (99.2) следует, что мощ- ность тока

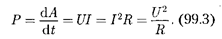
Если сила тока выражается в ампе- рах, напряжение — в вольтах, сопротив- ление — в омах, то работа тока выража- ется в джоулях, а мощность в ваттах. На практике применяются также внесис- темные единицы работы тока: ватт-час (Вт•ч),киловатт-час(кВт•ч);1 Вт•ч— работа тока мощностью 1 Вт в течение 1 ч; 1 Вт• ч = 3600 Вт• с = 3,6 • 103Дж;

1 кВт • ч = 103Вт • ч = 3,6 • 10° Дж.

Если ток проходит по неподвижно- му металлическому проводнику, то вся работа идет на его нагревание и, но за- кону сохранения энергии,

dQ = dA. (99.4)

Таким образом, используя выраже- ния (99.4), (99.1) и (99.2), получим

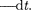dQ = 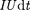= PRdt = (99.5)

R

Выражение (99.5) представляет со- бой закон Джоуля 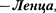экспери- ментально установленный независимо друг от друга Дж. Джоулем и Э. X. Лен-

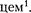
Выделим в проводнике элементар- ный цилиндрический объем dV = 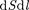(ось цилиндра совпадает с направлени- ем тока), сопротивление которого R =

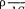— . По закону Джоуля 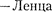за

dS

время 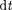в этом объеме выделится теп- лота

dQ PRdt = =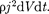

Количество теплоты, выделяющее- ся за единицу времени в единице объе- ма, называется удельной тепловой мощностью тока. Она равна

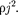= (99.6)

—

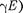Используя дифференциальную фор- му закона Ома (j — и соотношение р — 1 , получим

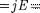
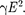(99.7)

Формулы (99.6) и (99.7) являются обобщенным выражением закона Джоуля 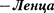в дифференциаль- ной форме, пригодным для любого про- водника.

Тепловое действие тока находит ши- рокое применение в технике, которое началось с открытия в 1873 г. русским инженером А.Н.Лодыгиным (1847 — 1923) лампы накаливания.

На нагревании проводников элект- рическим током основано действие электрических муфельных печей, элек- трической дуги [открыта русским ин-

женером В. В. Петровым (1761 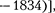контактной электросварки, бытовых электронагревательных приборов и т. д.

§ 100. Закон Ома