Поверхностный эффект в круглом проводе

Параметры электромагнитной системы : 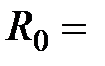1,5 см; 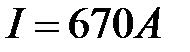; ; 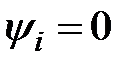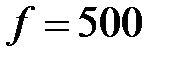Гц; ; .

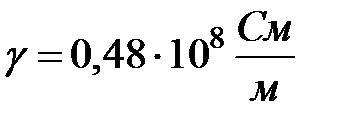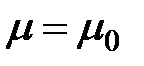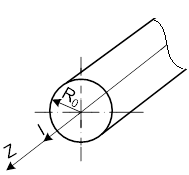
Рис.5.7

С учетом указанных в задании допущениях строится расчётная модель электромагнитной системы (рис.5.8)

Рис.5.8

Решение приведем в цилиндрической системе координат, ось которой совпадает с осью проводника и имеет направление, совпадающее с направлением тока в рассматриваемый момент времени. В такой системе координат с учетом принятых выше допущений электромагнитное поле в проводнике имеет только осевую составляющую напряженности электрического поля, направленную вдоль линии тока и только угловую составляющую напряженности магнитного поля, поверхностное значение которой на поверхности проводника, благородя осевой симметрии системы можно рассчитать на основании закона полного тока.

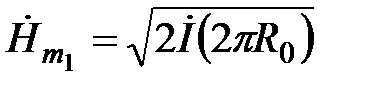. (5.1)

Запишем уравнение Максвелла для проводящей среды в комплексной форме

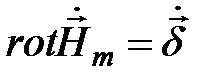, (5.2)

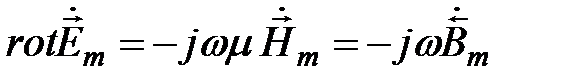(5.3)

совместно с остальными уравнениями электродинамики:

,

;

.

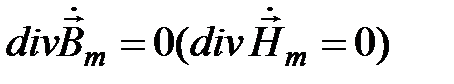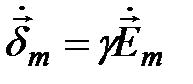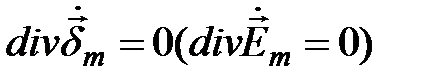Будем для решения использовать понятие векторного магнитного потенциала 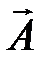, который вводится соотношениями

,

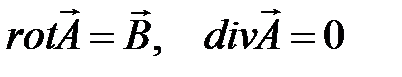тогда система уравнений поля сводится к уравнению для комплекса амплитуды векторного магнитного потенциала.

Перепишем (5.2)и (5.3) соответственно в виде

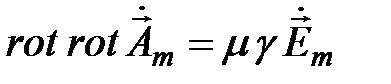(5.4)

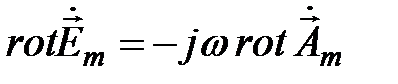. (5.5)

Из (*5.5) следует .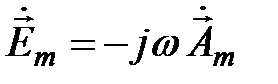

Учитывая векторное тождество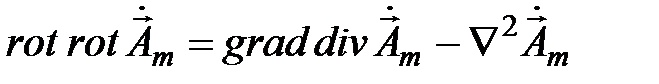

и что 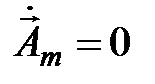, из (5.4*) получаем

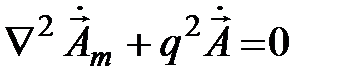(5.6)

где .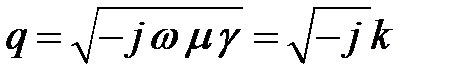

Вектор имеет только одну составляющую, т.е. 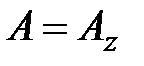. Поэтому (5.6) можно записать в виде

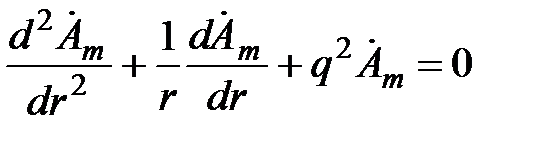(5.7)

Введя параметр 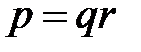получим уравнение Бесселя с комплексным аргументом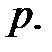

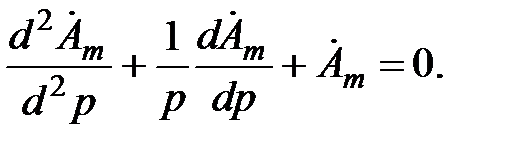(5.8)

Общее решение (5.8) можно записать в виде

,

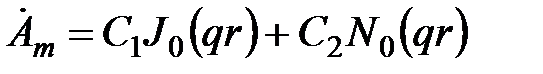где 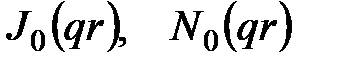- функция Бесселя нулевого порядка соответственно первого и второго рода.

Так как аргумент функции Бесселя общается в нуль на оси провода и 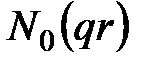= 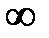, то функции Бесселя второго рода должна быть из решения исключена, т.е. постоянная 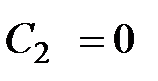. Тогда

.

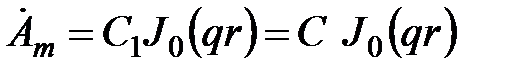Напряжённость магнитного поля определим с учетом правила дифференцирования функций Бесселя (см. приложения 2)

,

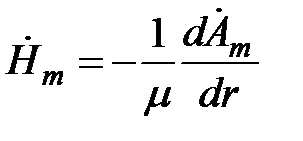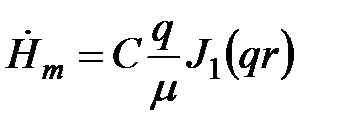. (5.9)

Определим постоянную интегрирования.

При ,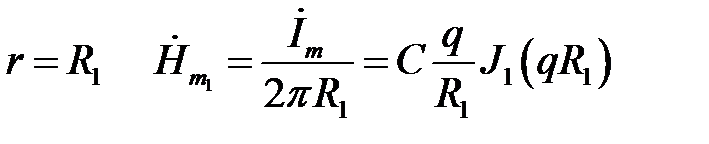

откуда .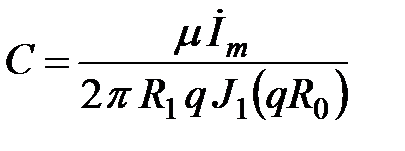

Подставляя выражение для С в (5.9), находим

.

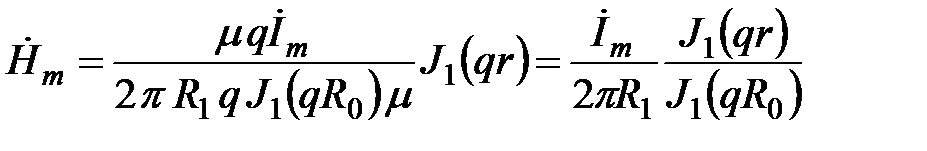Напряжённость электрического поля:

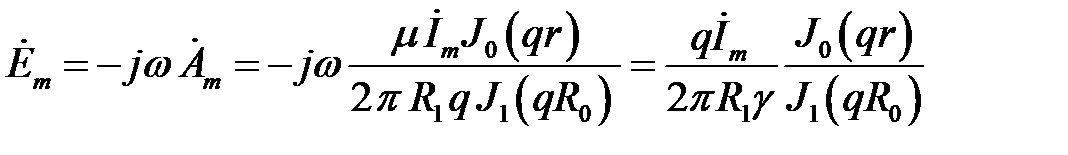
Комплекс амплитуды плотности тока:

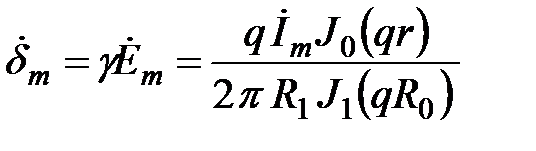
Определяем модуль вектор Пойнтинга на поверхность провода .

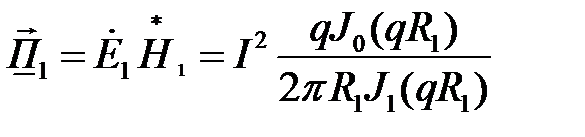
Используя теорему Умова-Пойнтинга, определяем: потери мощности на 1м длины проводника

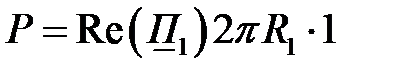Вт.

величины активного сопротивления и индуктивного сопротивления, обусловленного внутренней индуктивностью проводника определятся:

Анализ решения показывает, что перемен­ный ток по сечению ци­линдрического провода распределяется неравномерно.

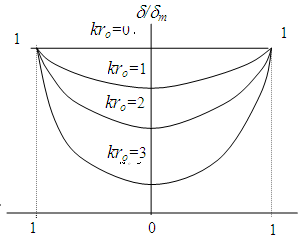
Поверхностный эффект возрас­тает с ростом частоты f, магнитной проницаемости m, удельной проводимости g. В технике сильных токов (на час­тоте 50 Гц) это явление сказывается незна­чи­тельно в медных и алюминиевых проводах большого сечения, и в сильной сте­пени - в сталь­ных (m_r>>1) проводах любого сечения.

Сопротивление проводника постоянному току или омиче­ское сопро­тивление определяется по формуле:

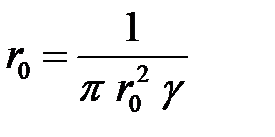[Ом/м].

Внутреннее комплексное сопротивление того же проводника перемен­ному току с учетом поверхностного эффекта может быть выражено через параметры поля:

.

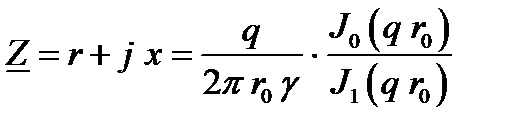Поверхностный эффект возрас­тает с ростом частоты f, магнитной проницаемости m, удельной проводимости g. В технике сильных токов (на частоте 50 Гц) это явление сказывается незна­чи­тельно в медных и алюминиевых проводах большого сечения, и в сильной сте­пени - в сталь­ных (m>>1) проводах любого сечения.

Практический интерес представляет отношение активного сопротивления провода к омическому r/r₀, количественно характеризующее поверхностный эффект в проводе.С ростом частоты fвследствие усиления поверхностного эффекта происходит увеличение активного сопротивления провода (r/r₀>1).