Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи плоской границы раздела двух диэлектриков
Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи плоской границы раздела двух диэлектриков
Рассмотрим поле оси, расположенной на расстоянии h от границы раздела двух диэлектриков с диэлектрическими проницаемостями e1 и e2 (рис.2.11а15а).
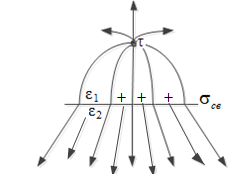
Вследствие разной поляризации диэлектриков на границе раздела выявятся связанные заряды, влияющие на поле в обеих средах. Поле создается свободным зарядом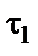 
, а также поверхностным связанным зарядом на границе раздела двух сред (рис.2.115б). Распределение связанных зарядов неизвестно.
В случае плоских, сферических и цилиндрических границ задача расчёта поля в кусочно-однородной среде решается методом зеркальных изображений.
Математическим обоснованием метода изображений является следствие теорема единственности решения.
Электростатическое поле по одну сторону некоторой поверхности S не изменится, если по другую сторону поверхности изменить параметры среды (например, заменить поводящую среду диэлектриком) и изменить расположение свободных зарядов так, чтобы на этой поверхности сохранились прежние граничные условия.
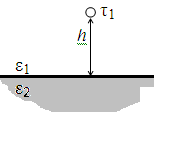
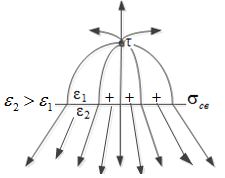
а) б)
Рис.2.15. К методу зеркальных изображений1
В случае плоских, сферических и цилиндрических границ задача расчёта поля в кусочно-однородной среде решается методом зеркальных изображений.
Математическим обоснованием метода изображений является следствие теорема единственности решения.
Электростатическое поле по одну сторону некоторой поверхности S не изменится, если по другую сторону поверхности изменить параметры среды (например, заменить поводящую среду диэлектриком) и изменить расположение свободных зарядов так, чтобы на этой поверхности сохранились прежние граничные условия.
Согласно этому методу вместо расчёта поля в неоднородной среде решают две эквивалентные задачи расчёта поля в однородных средах: первой и второй.
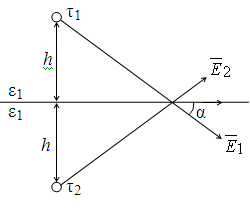
Расчёт поля в верхней части пространства ведется от двух зарядов: реального t1 и фиктивного t2, расположенных симметрично относительно границы раздела (рис.2.162а). Среда всюду имеет диэлектрическую проницаемость e1.
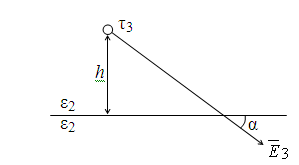
Расчёт поля в нижней части пронстранства ведется от заряда t3, расположенного в той же точке, что и t1 (рис.2.12б16б). Среда при этом всюду имеет проницаемость e2.
а) б)
Рис.2.1216
Величины и знаки зарядов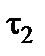 
и 
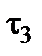определяются из требования неизменности граничных условий в исходной и эквивалентных задачах.
Граничные условия реальной задачи:
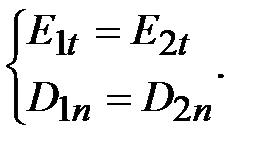
В расчётной моде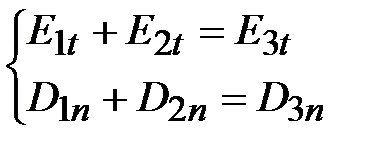ли:
или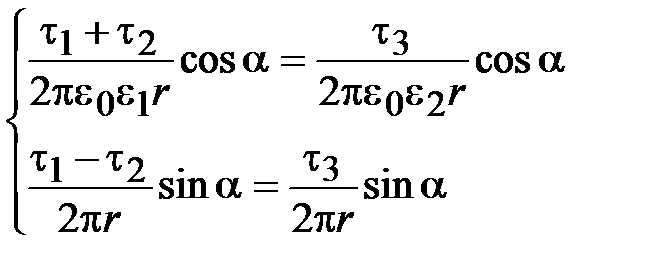 
.
Осюда получаем
; 
,
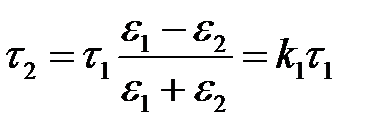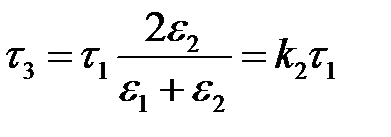Если относительную диэлектрическую проницаемость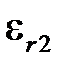 
устремить к бесконечности (вторая среда — проводник), то получим все соотношения для расчёта поля заряженной оси, расположенной над проводящей плоскостью. При этом с учетом 
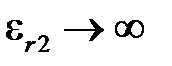имеем
.
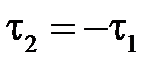В нижней полуплоскости поле равно нулю (проводнике).
Поле заряженной оси,