Дифракция на щели и квантовая теория света

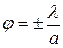Световые волны после щели распространяются во всех направлениях, но большая часть энергии приходится на сектор . При 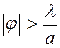интенсивность рассеянного излучения невелика, поэтому можно считать, что условие определяет граничное значение угла рассеивания. Значит, угол дифракции заключен в пределах

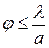. (7)

Чем уже щель (чем меньше а), тем шире пучок света, прошедшего через эту щель (тем больше ).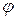

Опишем теперь эту же ситуацию, пользуясь представлением о пучке света как совокупности фотонов. Энергия и импульс фотона:

, .

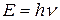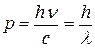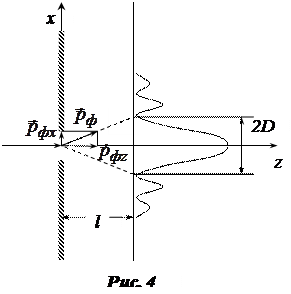
До прохождения через щель импульс фотона 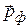был направлен вдоль оси z, поперечная составляющая импульса была равна нулю ( 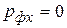), а неопределенность по координате х равна ∞. Расширение светового пучка при прохождении света через щель означает, что у фотона появляется составляющая импульса вдоль оси х ( 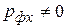). При этом неопределенность по координате 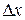будет равна ширине щели а (рис. 4). Считая, что угол 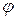определяется первым дифракционным минимумом, имеем (угол 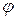- мал, ):

.

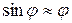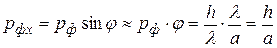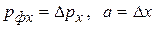. Следовательно,

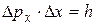. (8)

Мы учитывали только центральный максимум (см. рис. 2). С учетом максимумов более высоких порядков неопределенность по импульсу 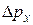может быть еще больше, и соотношение неопределенностей Гейзенберга нужно записать в виде:

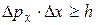. (9)

Смысл его состоит в том, что чем точнее определена одна из величин 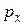или х, тем неопределенней становится другая. Фотон не может иметь одновременно абсолютно точных значений координаты и соответствующей проекции импульса. Соотношение (6), безусловно, применимо и для электронов и для других микрочастиц. Это один из важнейших законов микромира. Для удобства оценки результатов эксперимента можно ввести параметр

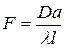(10)

Из рис. 4 следует, что 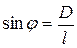. Поэтому .

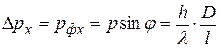Подставим найденное выражение для 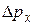в (8). После сокращения на h получаем, что при выполнении условия (8) параметр F должен быть равен 1:

.

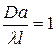Порядок выполнения работы

1. Установите на оптической скамье экран и дифракционную решетку

2. Включите лазер согласно прилагаемой инструкции и найдите положение экрана, при котором четко наблюдаются дифракционные максимумы.

3. Измерить линейкой расстояние а от решетки до экрана и расстояние 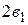между максимумами 1-го порядка и 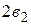максимумами 2-го порядка. Повторить измерения при других расстояниях а (по указанию преподавателя). Результаты запишите в таблицу 1.

Таблица 3

а, см	в, см
1. … 5.

4. Установите на оптической скамье микрометрическую щель так, чтобы пучок света проходил через щель. На расстоянии 0,9 м от щели установите экран с миллиметровыми делениями и добейтесь на экране отчетливой дифракционной картины.

5. Определите ширину 2D центрального максимума, измеряя расстояния между темными полосами, окаймляющими этот максимум.

6. Уменьшая ширину щели на 0,02 мм (ауд. 305) или на 0,2 (ауд. 309) и измеряя каждый раз 2D, записывайте измерения в таблицу 2.

7. Те же измерения проделайте пр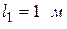и и 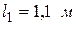. Данные запишите в таблицу 2.

Таблица 2

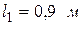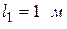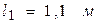а, мм	D, мм	F	а, мм	D, мм	F	а, мм	D, мм	F
1. …			1. … 10.			1. … 10.

8. Исследуйте зависимость интенсивности света от угла дифракции 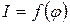для трех значений ширины щели (для ауд. 305 - 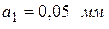, , 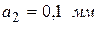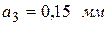; для ауд. 309 - 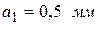, , 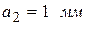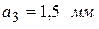). Для этого установите на расстоянии 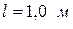от щели вместо экрана фотодиод, закрепленный в препаратоводитель. К фотодиоду подключите микроамперметр М95. Перемещая фотодиод в горизонтальном направлении, снимите зависимость фототока от координаты 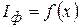. Центральному максимуму соответствует 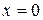. Нетрудно сообразить, что полученный график представляет собой зависимость 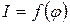в условных единицах 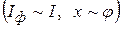. То же самое проделайте для других значений ширины щели.

Обработка результатов

1. По данным таблицы 1 рассчитайте длину волны 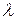, используя формулу (6). Результаты запишите в таблицу 3. Оцените погрешность измерения .

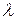Таблица 3

k		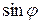d, м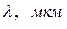

2. По данным таблицы 2 постройте графики зависимости .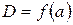

3. Для каждой пары значений а и D по формуле (10) рассчитайте величину F. При расчетах использовать длину волны, полученную в п.1. Определите 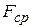. Рассчитайте погрешность 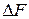как погрешность величины, измеряемой косвенным путем. Сравните полученный результат с ожидаемым результатом.

4. Постройте графики 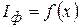. Сравните полученные графики с рис. 2.

Контрольные вопросы

1. В чем заключается явление дифракции?

2. Выведите условия максимума и минимума для случая дифракции на щели.

3. Запишите соотношение неопределенностей для координаты и импульса. Объясните его физический смысл.

4. Для каких еще величин можно записать соотношение неопределенностей?

5. От чего зависит энергия и импульс фотона? Запишите формулы.

6. Что называется дифракционной решеткой?

7. Что такое период решетки?

8. Как определить длину световой волны с помощью дифракционной решетки?

Литература

5. А.А.Детлаф, Б.М.Яворский. Курс физики, т. 3, М., «Высшая школа», 1979.

6. Г.А.Зисман, О.М.Тодес. Курс общей физики, т. 3, М., «Наука», 1978.

7. И.В.Савельев. Курс общей физики, т. 2, М., «Наука», 1978.

8. А.Н.Верхозин. Строение атома в общем курсе физики, Псков, 1983.

Лабораторная работа 2.05