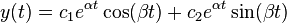Определитель Вронского. Формула Остроградского-Лиувилля.

Определителем Вронского W(x;y₁(x), y₂(x), ..., y_n(x)) называется определитель, первая строка которого образована функциями y₁(x), y₂(x), ..., y_n(x) из C_n-1[a, b] , а последующие строки образованы производными от функций предыдущей строки:

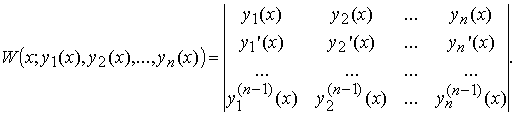
Справедливо следующее необходимое условие линейной зависимости функций.

Если функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b], то их определитель Вронского тождественно равен нулю на этом отрезке: W(x; y₁(x), y₂(x), ..., y_n(x)) ≡ 0 на [a;b].

Важно понимать, что обратное утверждение неверно. Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Однако, если определитель Вронского системы функций на некотором отрезке отличен от тождественного нуля, то система функций линейно независима на этом отрезке.

Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.

Рассмотрим две функции:

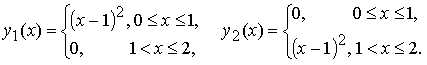
Эти функции линейно независимы на [0, 2]. Действительно:

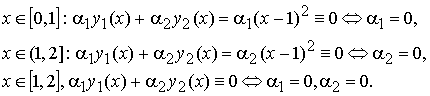
Вычислим определитель Вронского W(x;y₁(x), y₂(x)) на [0, 2]:

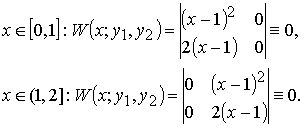
Итак, функции линейно независимы на [0, 2], а W(x; y₁(x), y₂(x)) ≡ 0 на [0, 2].

Этот пример означает, что тождественное равенство нулю определителя Вронского системы функций является необходимым условием линейной зависимости системы функций, но не является достаточным условием линейной зависимости системы функций.

С другой строны, отличие от тождественного нуля определителя Вронского системы функций является достаточным условием условием линейной независимости системы функций.

(Ведь если бы она была бы линейно зависима, то определитель Вронского был бы тождественным нулём).

Определителем Вронского вектор-функций Y₁(x), Y₂(x), ..., Y_n(x),

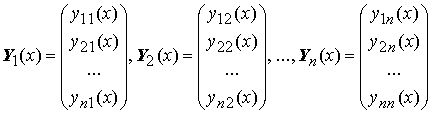
называется определитель W[x; Y₁, Y₂, ..., Y_n], заданный равенством

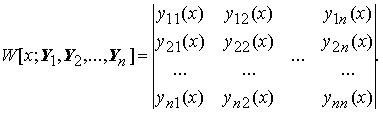
Формула Лиуви́лля-Острогра́дского — формула, связывающая определитель Вронского (вронскиа́н) для решений дифференциального уравнения и коэффициенты в этом уравнении.

Пусть есть дифференциальное уравнение вида

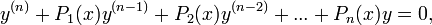
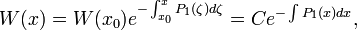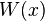тогда где — определитель Вронского

Для линейной однородной системы дифференциальных уравнений

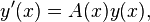где 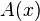— непрерывная квадратная матрица порядка 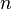, справедлива формула Лиувилля-Остроградского

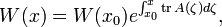где 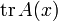— след матрицы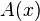

Построение общего решения линейного однородного уравнения 2 – го порядка с постоянными коэффициентами.

Однородное уравнение второго порядка:

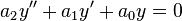
интегрируется следующим образом:

Пусть 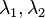— корни характеристического уравнения.

,

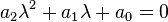являющегося квадратным уравнением.

Вид общего решения однородного уравнения зависит от значения дискриминанта :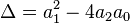

· при 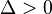уравнение имеет два различных вещественных корня

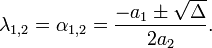
Общее решение имеет вид:

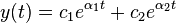
· при 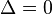— два совпадающих вещественных корня

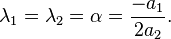
Общее решение имеет вид:

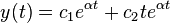
· при 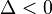существуют два комплексно сопряженных корня

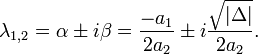
Общее решение имеет вид: