Первообразная и неопределенный интеграл.
Первообразная и неопределенный интеграл.
Функция 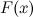 называется первообразной для функции
называется первообразной для функции 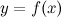 на промежутке
на промежутке 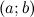 , конечном или бесконечном, если функция
, конечном или бесконечном, если функция 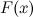 дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
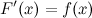
Функция F(x) называется первообразной для функции f(x), если справедливо равенство F’(x)=f(x).
В общем случает, если для функции f(x) есть первообразная F(x), для которой выполняется равенство, то f(x) +с так же первообразная для функции f(x), где с – произвольная константа.
Функция вида F(x)+c – семейство первообразных.
(О бесконечном множестве первообразных для функции)
Если функция 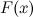 является первообразной для функции
является первообразной для функции 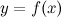 на некотором промежутке, то и функция
на некотором промежутке, то и функция 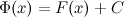 , где
, где 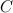 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции 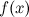 на рассматриваемом промежутке.
на рассматриваемом промежутке.
(Об общем виде первообразной для функции)
Если функции 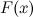 и
и 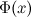 - две любые первообразные функции
- две любые первообразные функции 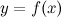 , то их разность равна некоторой постоянной, то есть
, то их разность равна некоторой постоянной, то есть
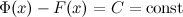
Теорема 1.Пусть F(x) некоторая первообразная для f(x), тогда все первообразные представлены в виде семейства f(x)+с, где с – константа.
Док-во. Пусть F(x) –первообразная для f(x).
Фи(х)= f(x)
По условию теоремы F(x) так же первообразная f(x)= F(x)
Вычтем: фи(х)- f(x)=0
По св-ву производной:
(фи(х)- f(x))’=0
Следовательно:
фи(х)- f(x)=с
фи(х)- f(x)+с
Следствие: любые две первообразные для одной и той же функции отличаются разве лишь на постоянное число.
Семейство первообразных f(x)+c функции f(x) называют неопределенными интегралами и обозначают значком интеграла.
Теорема 2(без док-ва).
Если f(x) подинтегральная функция непрерывная на некотором промежутке, то для нее существет первообразная и неопределенный интеграл.
Совокупность всех первообразных функции 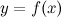 , определенных на заданном промежутке, называется неопределенным интегралом от функции
, определенных на заданном промежутке, называется неопределенным интегралом от функции 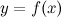 и обозначается символом
и обозначается символом 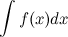 . То есть
. То есть
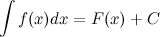
Знак 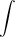 называется интегралом,
называется интегралом, 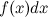 - подынтегральным выражением,
- подынтегральным выражением, 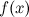 - подынтегральной функцией, а
- подынтегральной функцией, а  - переменной интегрирования.
- переменной интегрирования.
Операция нахождения первообразной или неопределенного интеграла от функции 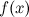 называется интегрированием функции
называется интегрированием функции 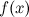 . Интегрирование представляет собой операцию, обратную дифференцированию.
. Интегрирование представляет собой операцию, обратную дифференцированию.
Т. о. с геометрической точки зрения неопределенный интеграл есть семейство интегралов кривых, полученных х в результате сдвига интегральной кривой у= f(x) в направлении оси ОУ вверх/вниз на отрезок произвольной длины с.
Теорема о среднем.
Если f(x) непрерывна на отрезке [a,b], то существует точка 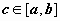 , такая что
, такая что 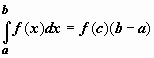 .
.  Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения.
Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. 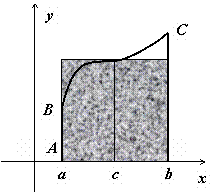 Тогда
Тогда 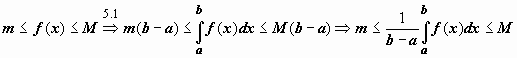 . Число
. Число 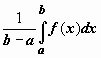 заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между mи M. Таким образом, существует точка
заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между mи M. Таким образом, существует точка 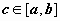 , такая что
, такая что 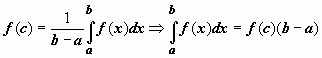 .
.
 Это свойство имеет простую геометрическую интерпретацию: если
Это свойство имеет простую геометрическую интерпретацию: если 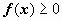 непрерывна на отрезке [a,b], то существует точка
непрерывна на отрезке [a,b], то существует точка 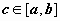 такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).
такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).
Важное следствие
| Утверждение: |
Пусть 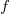 — непрерывна на — непрерывна на 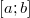 . Тогда на этом отрезке у неё существует неопределённый интеграл. . Тогда на этом отрезке у неё существует неопределённый интеграл. |
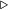 |
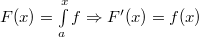 В силу непрерывности функции на отрезке и теоремы Барроу В силу непрерывности функции на отрезке и теоремы Барроу 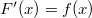 — одна из первообразных. Значит, неопределённый интеграл существует. — одна из первообразных. Значит, неопределённый интеграл существует. |
Формула Ньютона-Лейбница
| Теорема (формула Ньютона-Лейбница): |
Пусть 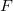 дифференцируема на дифференцируема на 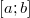 , её производная , её производная 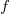 интегрируема на этом же отрезке. Тогда интегрируема на этом же отрезке. Тогда 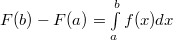 |
| Доказательство: |
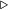 |
Так как 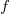 — интегрируема, то — интегрируема, то 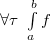 равен пределу интегральных сумм при любой системе промежуточных точек для равен пределу интегральных сумм при любой системе промежуточных точек для  . Поэтому, если . Поэтому, если  — разбиение — разбиение 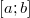 , то , то 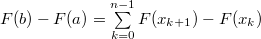 . Так как . Так как 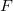 дифференцируема, то, применив для каждого промежутка из разбиения формулу Лагранжа, получим: дифференцируема, то, применив для каждого промежутка из разбиения формулу Лагранжа, получим: 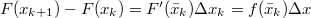 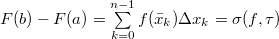 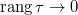 , следовательно, правая часть стремится к интегралу, левая — постоянна. Значит, в пределе, получаем нужную формулу. , следовательно, правая часть стремится к интегралу, левая — постоянна. Значит, в пределе, получаем нужную формулу. |
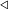 |
Следствие
Объединяя эту теорему со следствием к теореме Барроу получаем следующий факт:
| Утверждение: |
Пусть 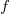 — непрерывна на — непрерывна на 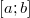 , , 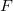 — одна из первообразных. Тогда — одна из первообразных. Тогда 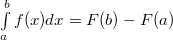 |
Формулы
]Вычисление определенного интеграла по частям
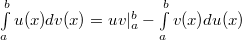
Формула Ньютона-Лейбница.
Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции 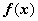 , то
, то 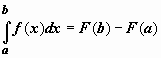 .
.
 Док-во. Мы установили, что функция
Док-во. Мы установили, что функция 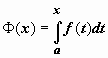 - первообразная непрерывной f(x). Так как F(x) - тоже первообразная, то Ф(x) = F(x) + C. Положим в этом равенстве x = a. Так как
- первообразная непрерывной f(x). Так как F(x) - тоже первообразная, то Ф(x) = F(x) + C. Положим в этом равенстве x = a. Так как 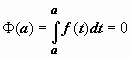 , то
, то 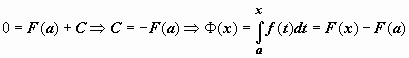 . В равенстве
. В равенстве 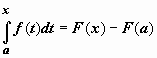 переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x , верхний предел x обозначим b. Окончательно,
переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x , верхний предел x обозначим b. Окончательно, 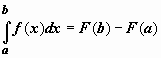 .
.
 Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом:
Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом: 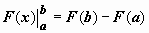 (здесь
(здесь 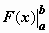 читается как "подстановка от a до b"), поэтому формулу Ньютона-Лейбница обычно записывают так:
читается как "подстановка от a до b"), поэтому формулу Ньютона-Лейбница обычно записывают так: 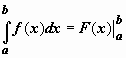 .
.
 Пример применения формулы Ньютона-Лейбница:
Пример применения формулы Ньютона-Лейбница: 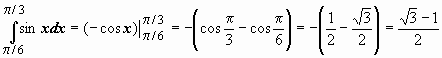 .
.
Первообразная и неопределенный интеграл.
Функция 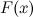 называется первообразной для функции
называется первообразной для функции 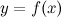 на промежутке
на промежутке 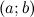 , конечном или бесконечном, если функция
, конечном или бесконечном, если функция 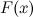 дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
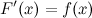
Функция F(x) называется первообразной для функции f(x), если справедливо равенство F’(x)=f(x).
В общем случает, если для функции f(x) есть первообразная F(x), для которой выполняется равенство, то f(x) +с так же первообразная для функции f(x), где с – произвольная константа.
Функция вида F(x)+c – семейство первообразных.
(О бесконечном множестве первообразных для функции)
Если функция 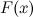 является первообразной для функции
является первообразной для функции 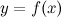 на некотором промежутке, то и функция
на некотором промежутке, то и функция 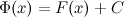 , где
, где 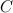 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции 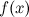 на рассматриваемом промежутке.
на рассматриваемом промежутке.
(Об общем виде первообразной для функции)
Если функции 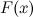 и
и 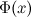 - две любые первообразные функции
- две любые первообразные функции 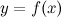 , то их разность равна некоторой постоянной, то есть
, то их разность равна некоторой постоянной, то есть
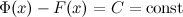
Теорема 1.Пусть F(x) некоторая первообразная для f(x), тогда все первообразные представлены в виде семейства f(x)+с, где с – константа.
Док-во. Пусть F(x) –первообразная для f(x).
Фи(х)= f(x)
По условию теоремы F(x) так же первообразная f(x)= F(x)
Вычтем: фи(х)- f(x)=0
По св-ву производной:
(фи(х)- f(x))’=0
Следовательно:
фи(х)- f(x)=с
фи(х)- f(x)+с
Следствие: любые две первообразные для одной и той же функции отличаются разве лишь на постоянное число.
Семейство первообразных f(x)+c функции f(x) называют неопределенными интегралами и обозначают значком интеграла.
Теорема 2(без док-ва).
Если f(x) подинтегральная функция непрерывная на некотором промежутке, то для нее существет первообразная и неопределенный интеграл.
Совокупность всех первообразных функции 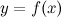 , определенных на заданном промежутке, называется неопределенным интегралом от функции
, определенных на заданном промежутке, называется неопределенным интегралом от функции 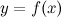 и обозначается символом
и обозначается символом 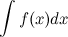 . То есть
. То есть
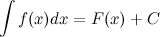
Знак 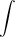 называется интегралом,
называется интегралом, 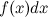 - подынтегральным выражением,
- подынтегральным выражением, 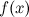 - подынтегральной функцией, а
- подынтегральной функцией, а  - переменной интегрирования.
- переменной интегрирования.
Операция нахождения первообразной или неопределенного интеграла от функции 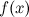 называется интегрированием функции
называется интегрированием функции 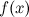 . Интегрирование представляет собой операцию, обратную дифференцированию.
. Интегрирование представляет собой операцию, обратную дифференцированию.
Т. о. с геометрической точки зрения неопределенный интеграл есть семейство интегралов кривых, полученных х в результате сдвига интегральной кривой у= f(x) в направлении оси ОУ вверх/вниз на отрезок произвольной длины с.
