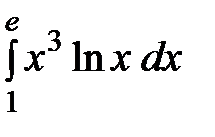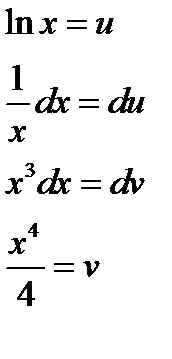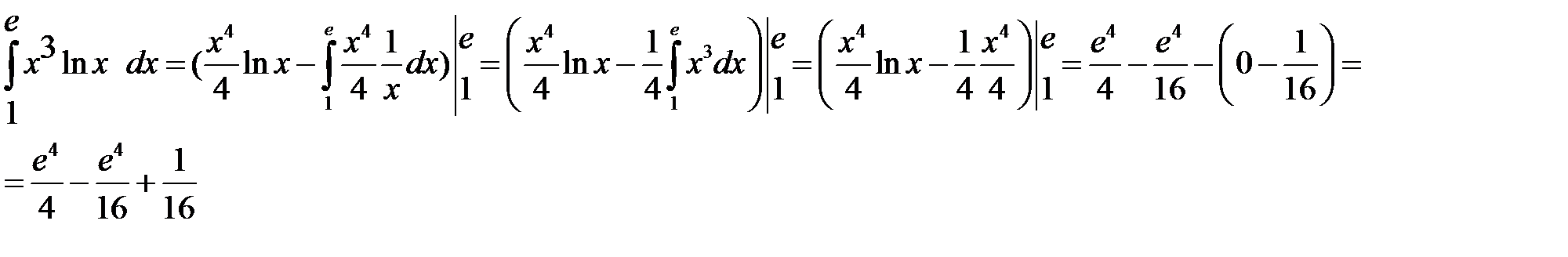Интегрирование рациональных функций от тригонометрических функций.
Пример 1.Найти неопределенный интеграл
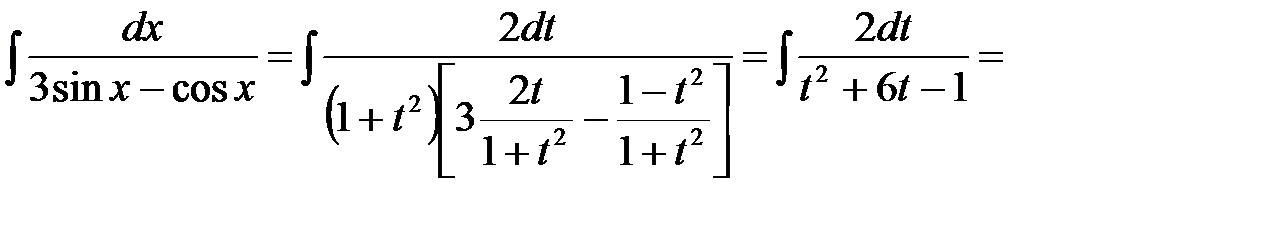
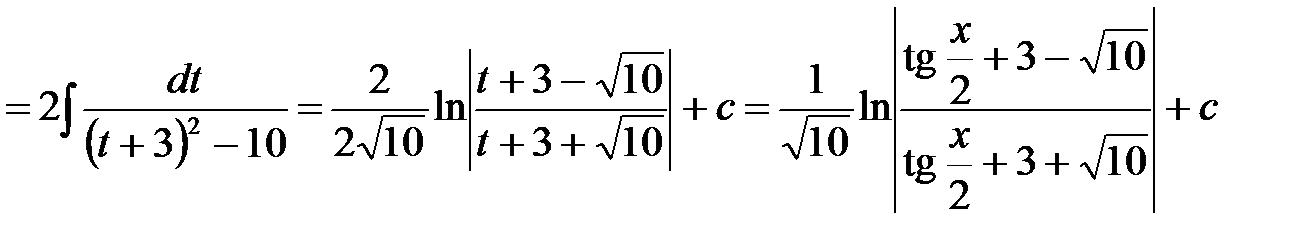 .
.
Пример 2.Найти неопределенный интеграл
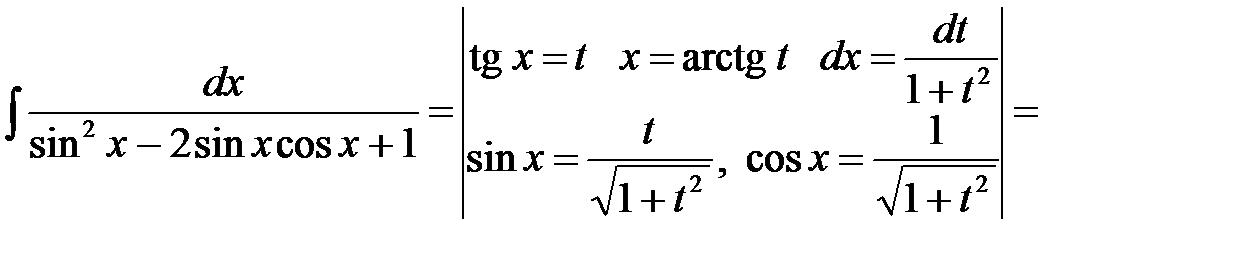
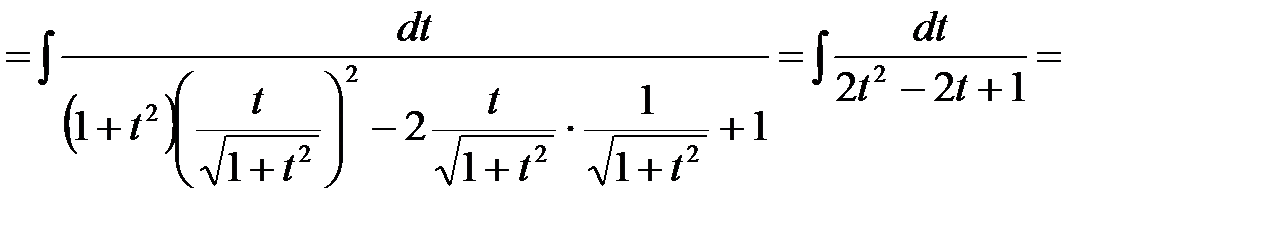
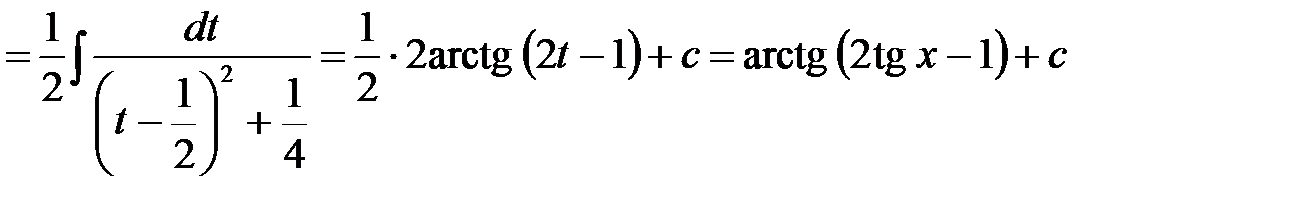 .
.
Пример 3. Найти неопределенный интеграл
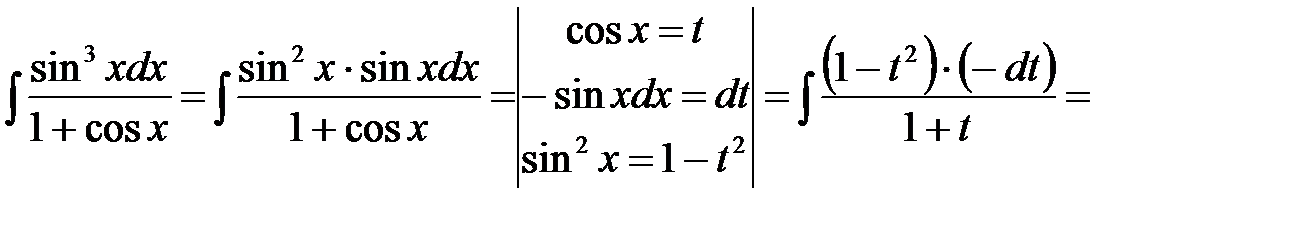
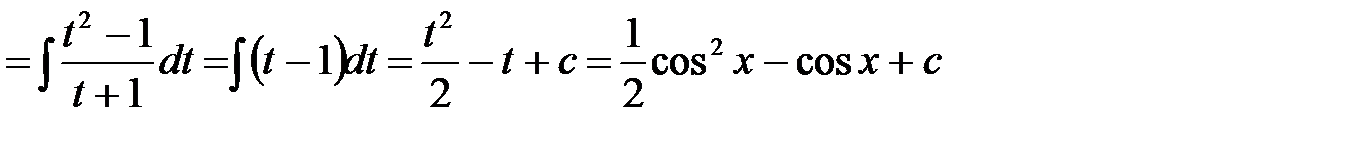 .
.
Пример 4.Найти неопределенный интеграл
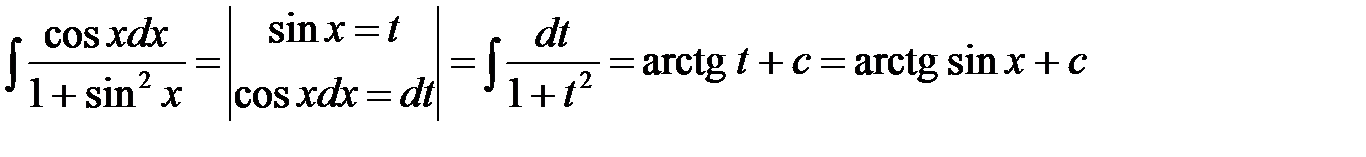 .
.
Пример 5.Найти неопределенный интеграл
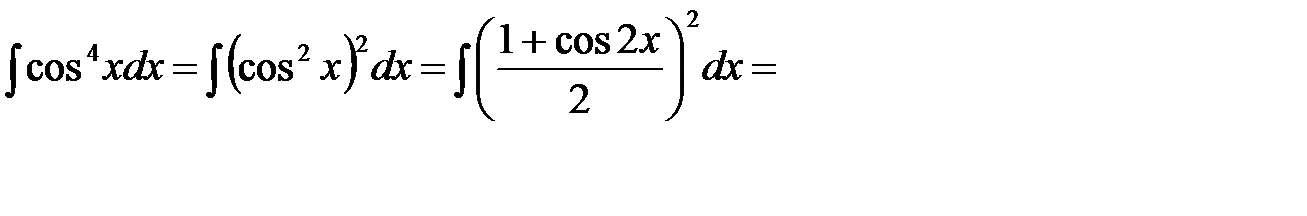
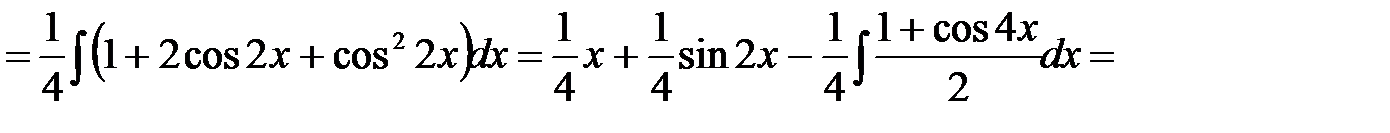
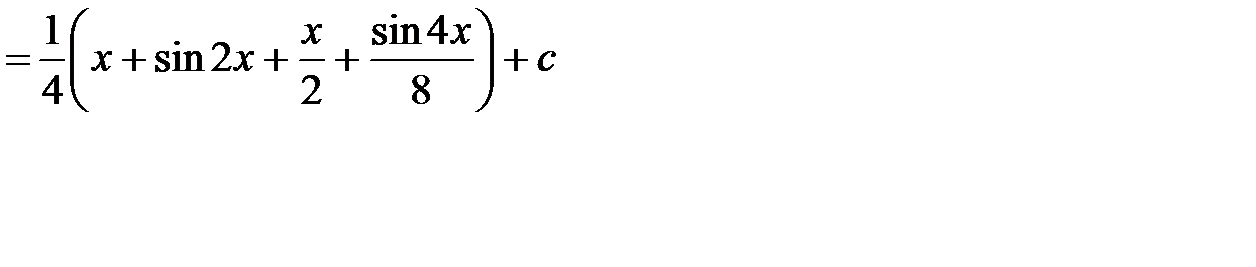 .
.
Пример 6. Найти неопределенный интеграл 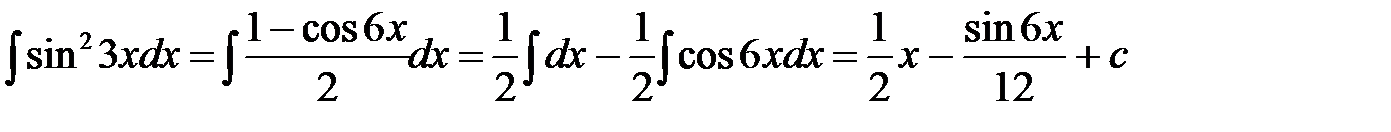 .
.
Пример 7. Найти неопределенный интеграл
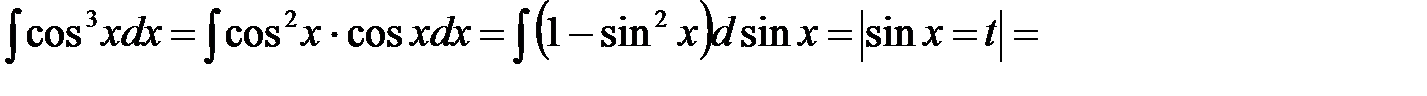
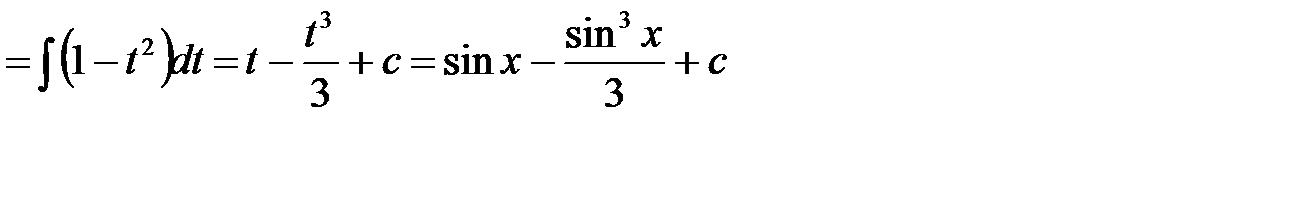 .
.
Пример 8. Найти неопределенный интеграл: 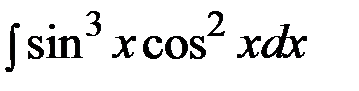 .
.
Решение: Здесь функция sinxстоит в нечетной степени, поэтому 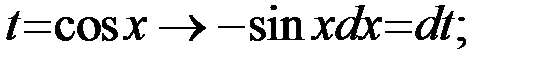
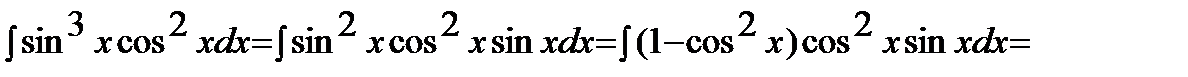
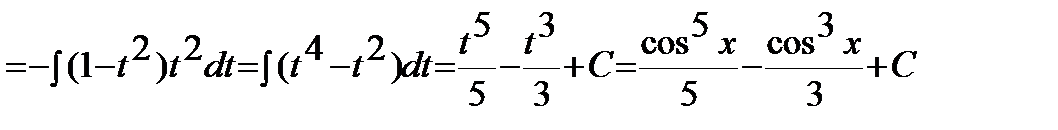 ;
;
Пример 9. Найти неопределенный интеграл
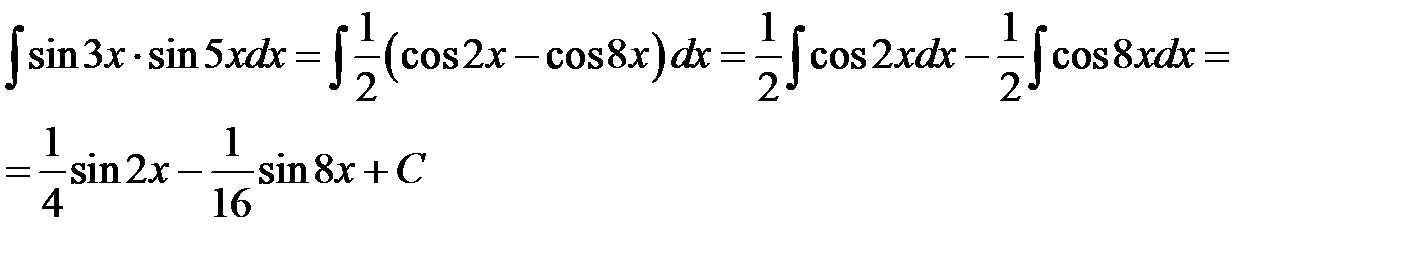
Пример 10. Найти неопределенный интеграл
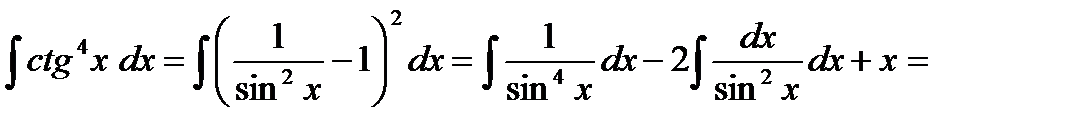
= - 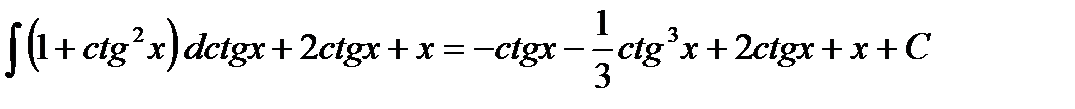
Пример 11. Найти неопределенный интеграл
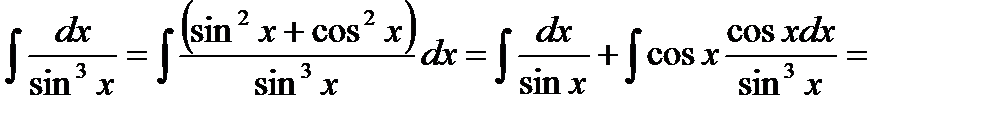
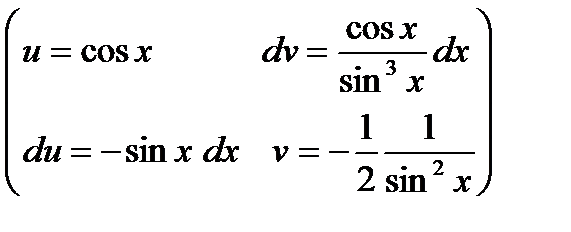 =
= 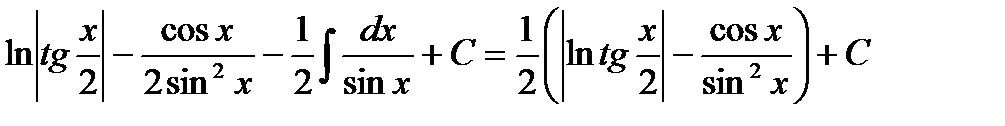 .
.
Интегрирование рациональных функций некоторых иррациональностей
Пример 1. Найти неопределенный интеграл 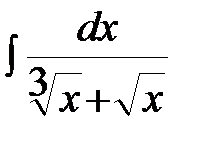 .
.
Решение:
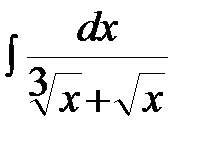
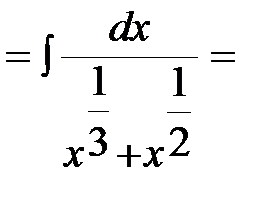
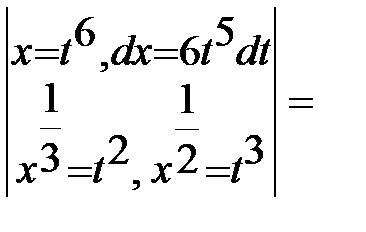
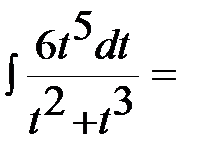
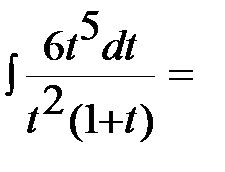
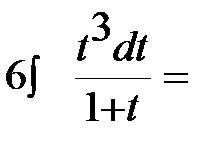
В подынтегральном выражении выделим целую часть: 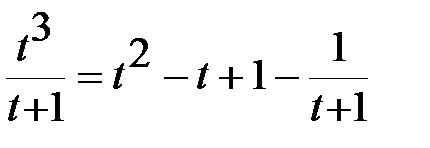 ,
,
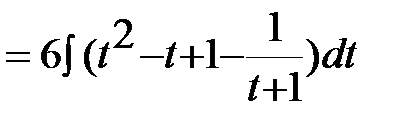
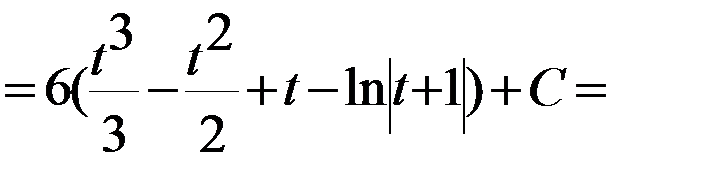
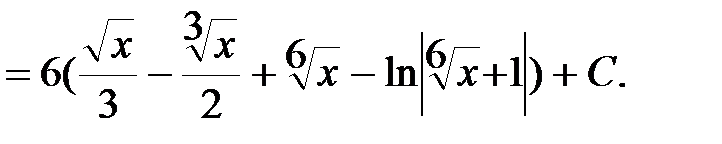 .
.
Пример 2. Найти неопределенный интеграл 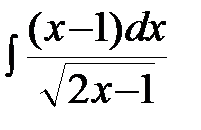 .
.
Решение:Сделаем следующую замену переменных: 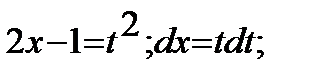
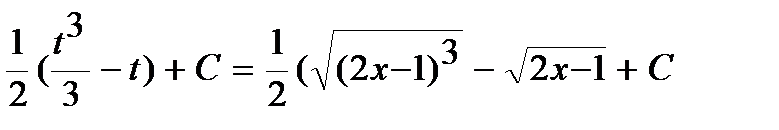 .
.
Пример 3. Найти неопределенный интеграл 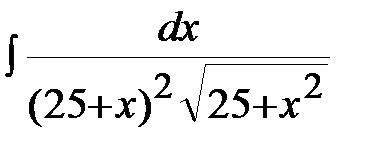 .
.
Решение:Замена 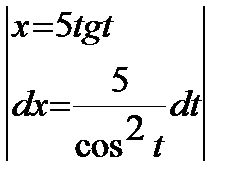 интеграл примет вид
интеграл примет вид 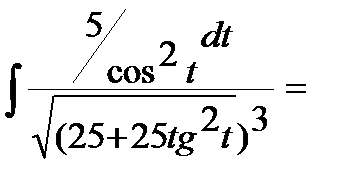
= 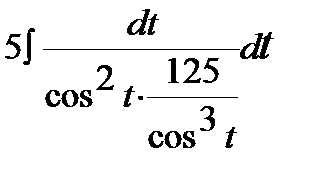 =
= 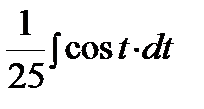 =
= 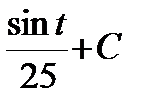 =
= 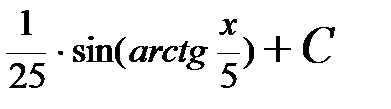 =
=
= 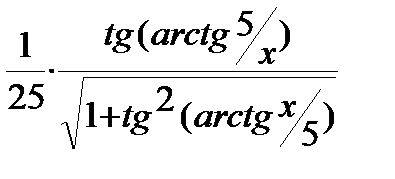 +С=
+С= 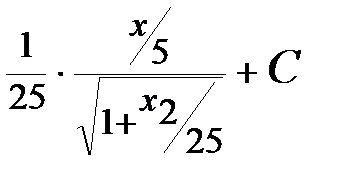 =
= 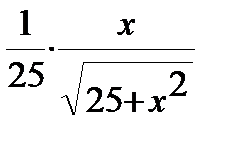 +С.
+С.
Пример 4. Найти неопределенный интеграл 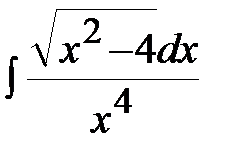 .
.
Решение:Замена 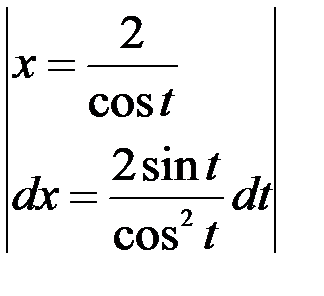 тогда
тогда 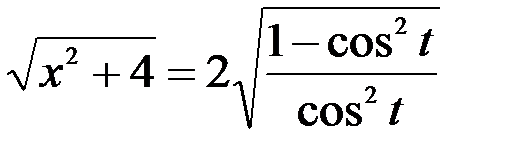 =
= 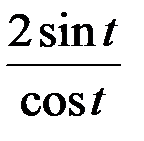 .
. 
Интеграл примет вид 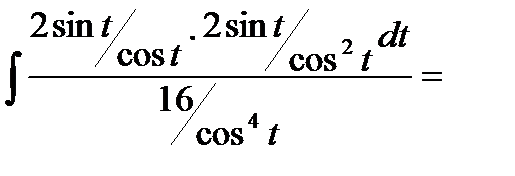
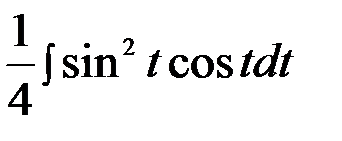 =
=
= 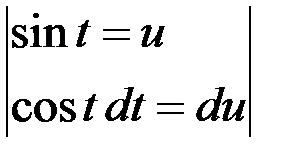 =
= 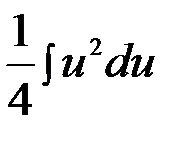 =
= 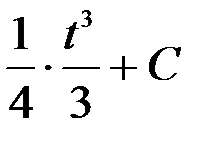 =
= 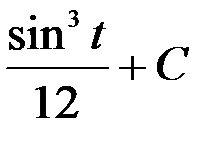 =
= 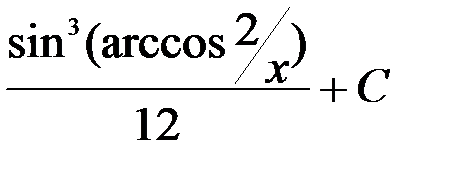
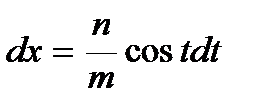 .
.
Пример 5. Найти неопределенный интеграл 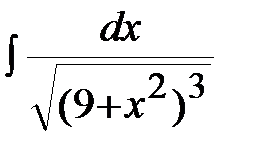 .
.
Решение:Замена 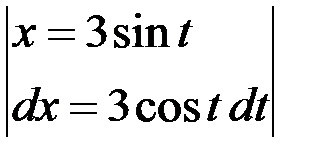 Тогда интеграл примет вид
Тогда интеграл примет вид 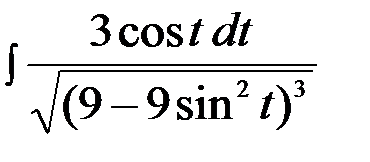 =
=
= 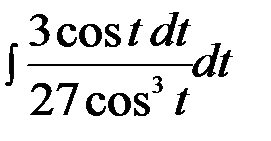 =
= 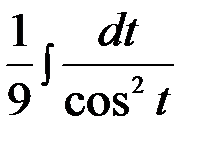 =
= 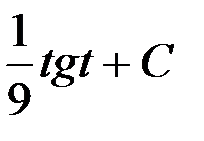 =
= 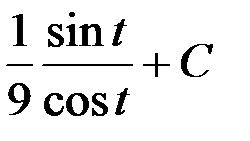 =
= 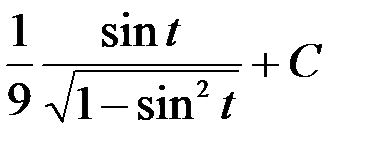 =
=
= 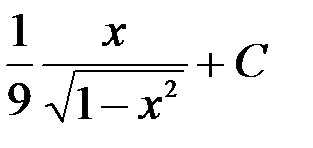 .
.
Определенный интеграл
1.Используя формулу Ньютона-Лейбница, вычислить интегралы:
1). 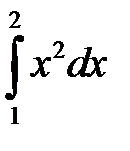
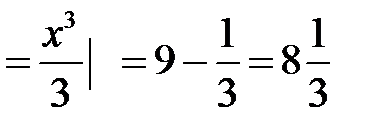

2). 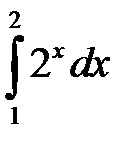 =
= 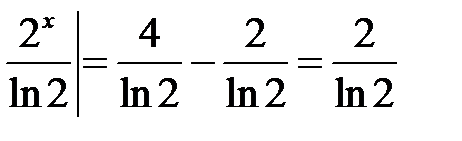
3). 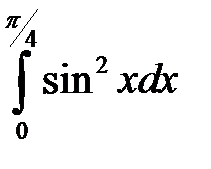
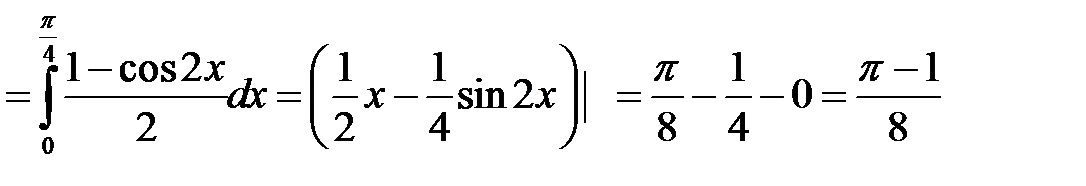
4) 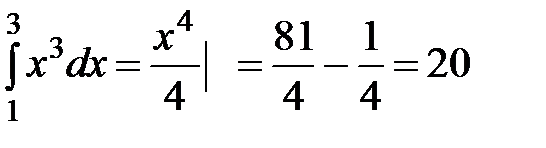
5) 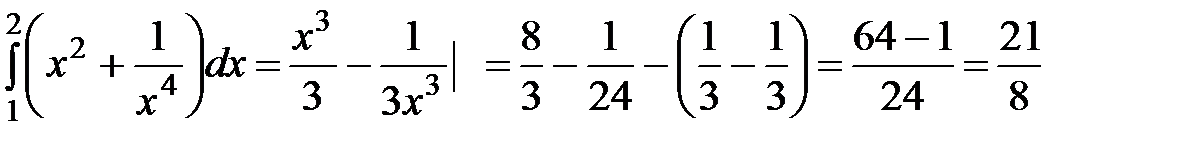
6) 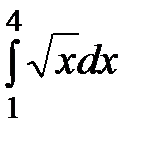
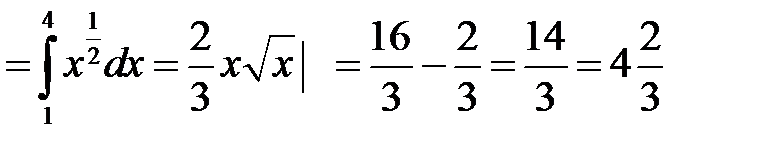
7) 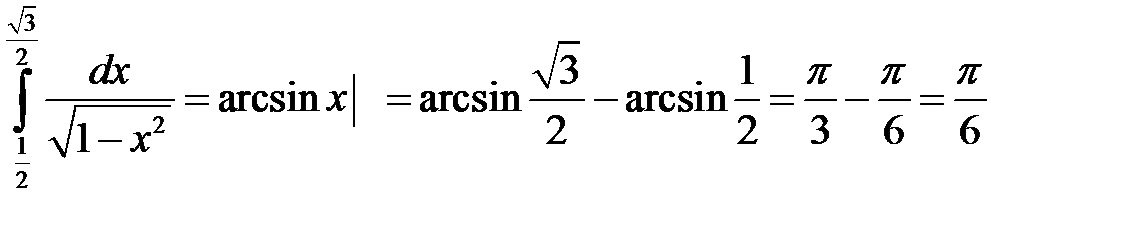
8) 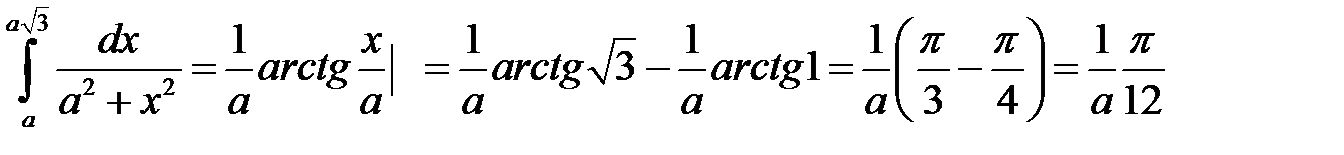
9) 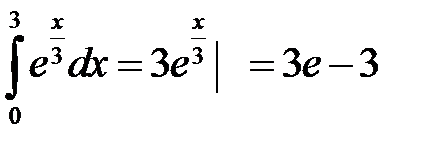

10) 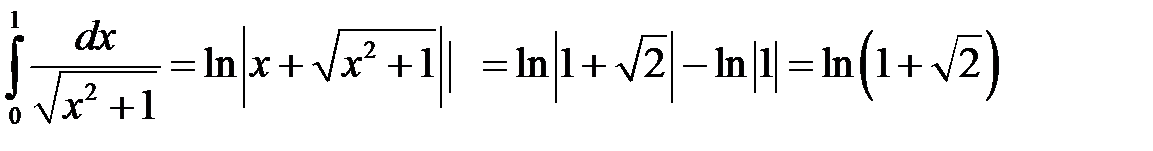

11) 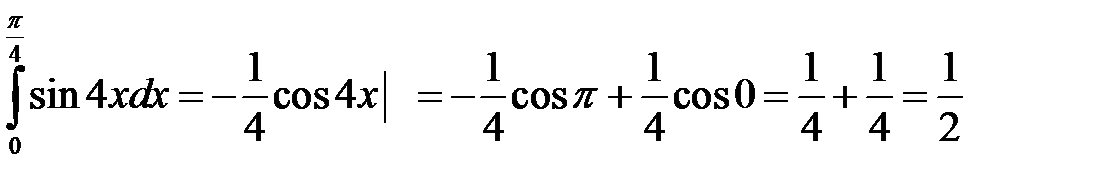
12) 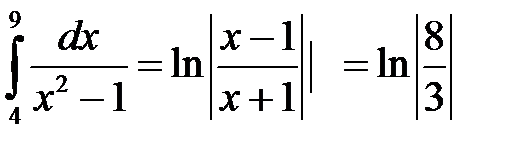
13) 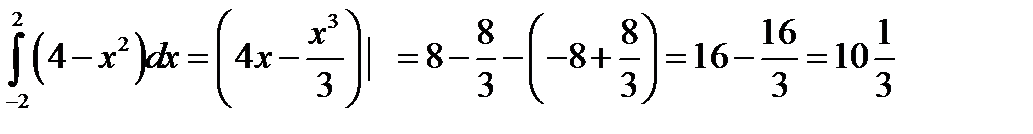
14) 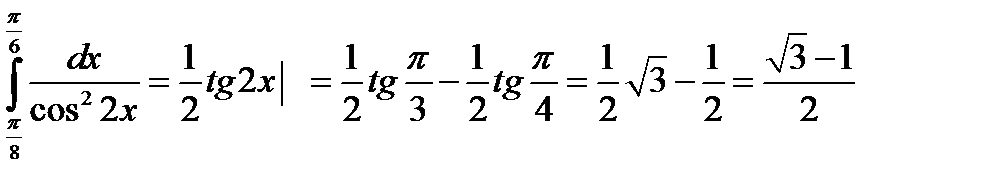
15) 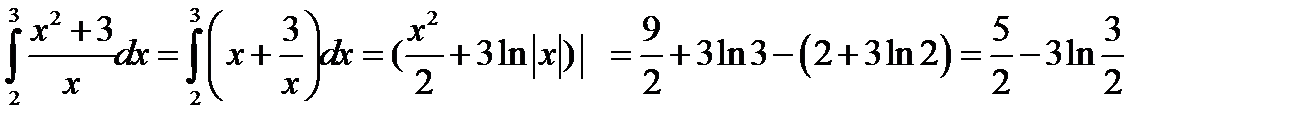
Вычисление определенного интеграла методом замены
1. 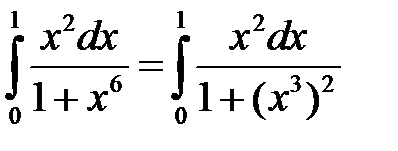
Положим 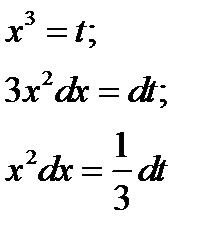
Вычислим новые пределы интегрирования
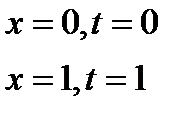
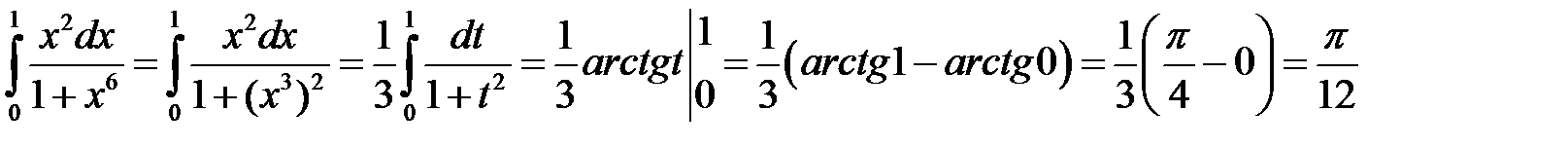
2. 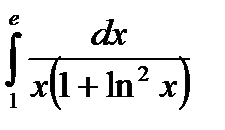
Положим 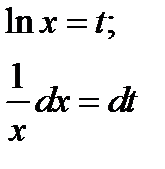
Вычислим новые пределы интегрирования
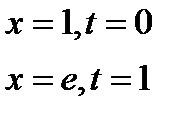

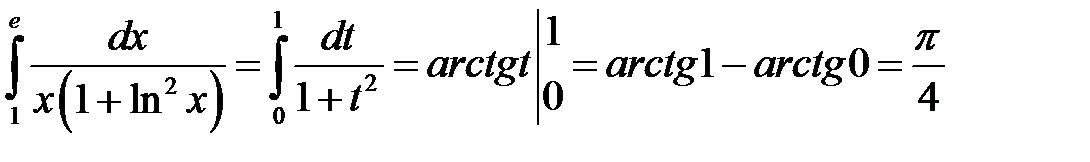
3. 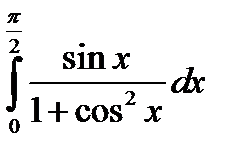
Положим 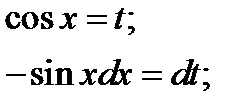
Вычислим новые пределы интегрирования
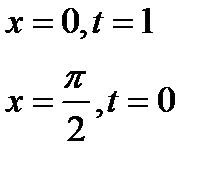
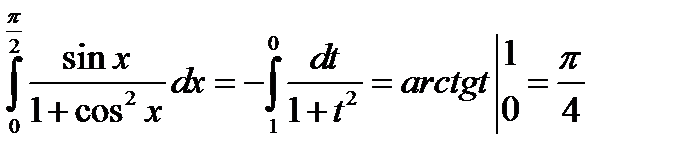
4. . Вычислить определенный интеграл : 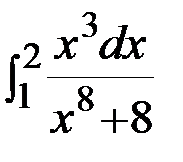 .
.
Решение:Сделаем замену переменных 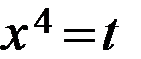 . Тогда
. Тогда
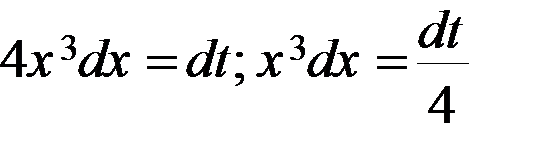 .
.
Найдем новые пределы интегрирования, подставив в формулу 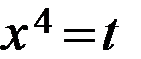 вместо x сначала единицу, а затем двойку, получим таблицу для нахождения новых пределов:
вместо x сначала единицу, а затем двойку, получим таблицу для нахождения новых пределов:
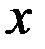 | ||
 |
Итак, 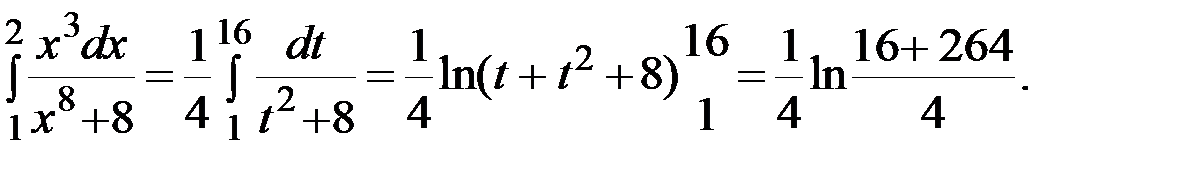
5. Вычислить определенный интеграл : 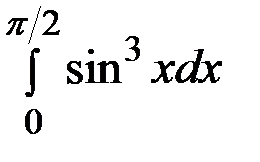 .
.
Решение:Положив 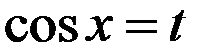 , Тогда находим,
, Тогда находим, 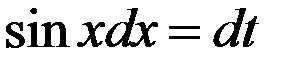 и
и 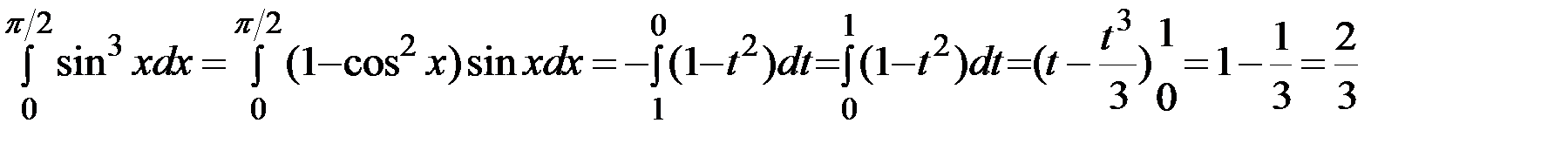
6. Вычислить определенный интеграл:
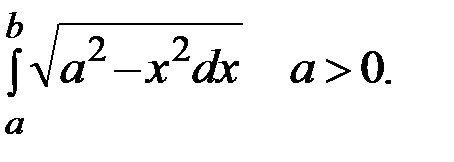
Решение: Сделаем следующую замену переменных: 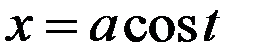 . Тогда
. Тогда 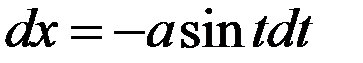 .
.
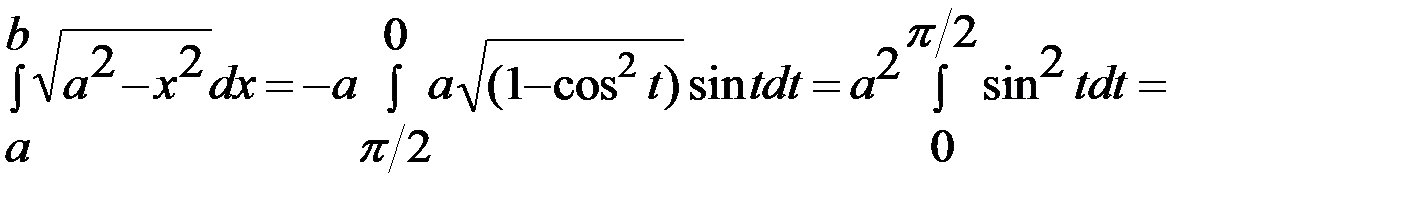
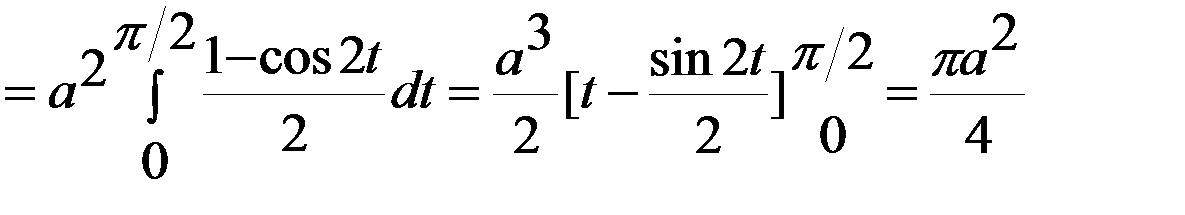 (новые пределы интегрирования были найдены из уравнений:
(новые пределы интегрирования были найдены из уравнений: 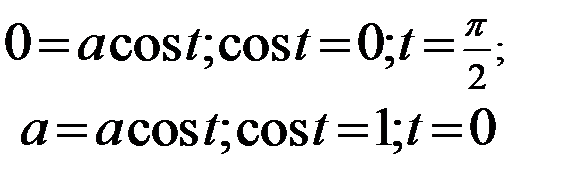
7.Вычислить интеграл 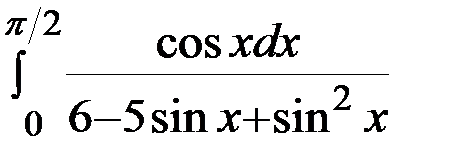 .
.
Решение: Применим подстановку: 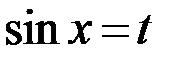 ,
, 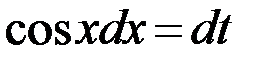 , если
, если 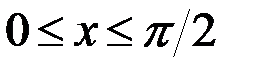 , то
, то 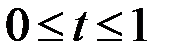 . Следовательно,
. Следовательно,
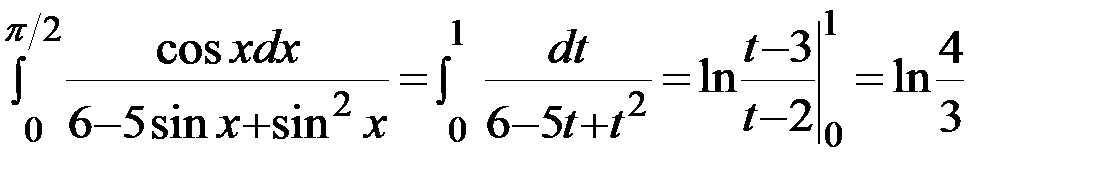 .
.
8.Вычислить интеграл 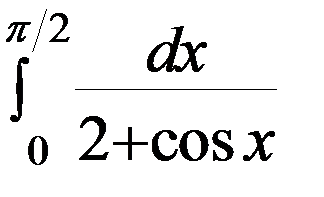 .
.
Решение: Применим подстановку: 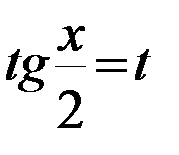 ,
, 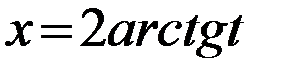 ,
, 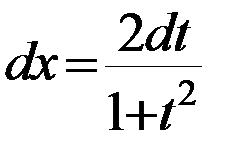 , если
, если 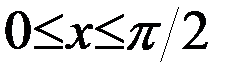 , то
, то 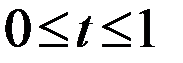 .
.
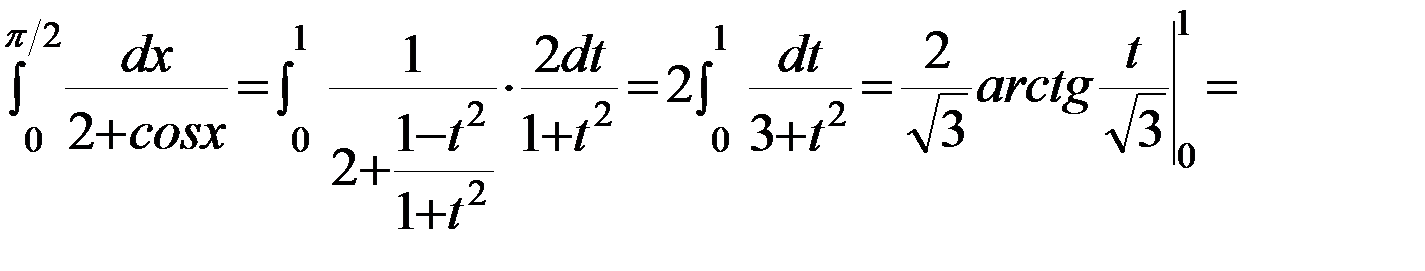
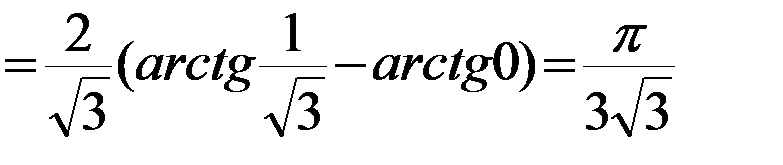 .
.
Метод по частям для вычисления определенного интеграла.
1. Вычислить определенный интеграл
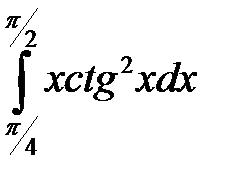
Решение. Используем тригонометрическую формулу 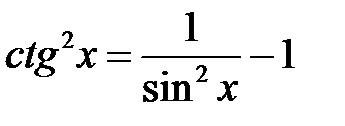 ,
,
получаем интеграл:


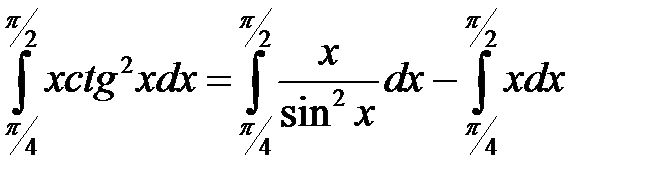
2. Вычислим 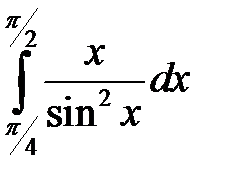 методом по частям. Положим
методом по частям. Положим
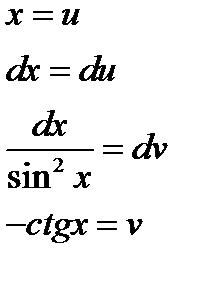
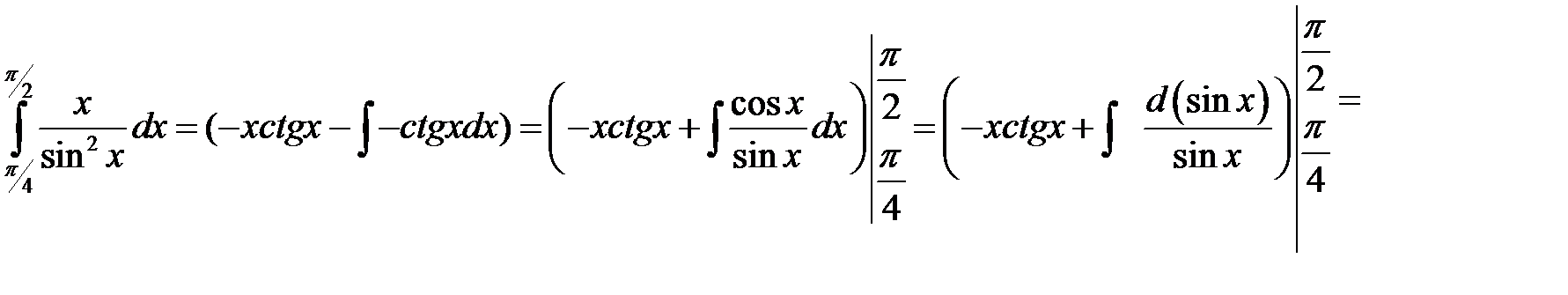
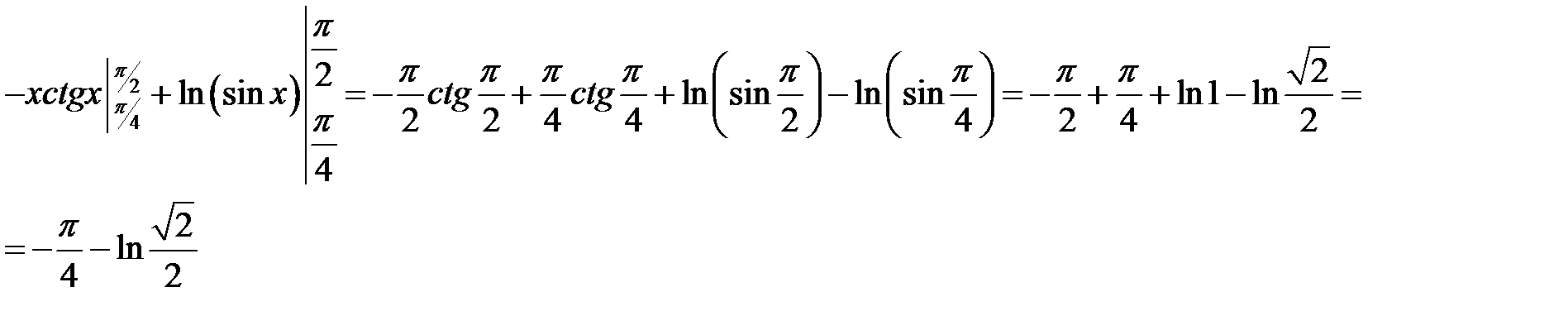 Пример 3.
Пример 3.
Вычислить определенный интеграл: 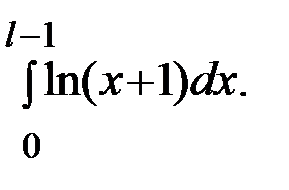
Решение:В формуле интегрирования по частям положим:
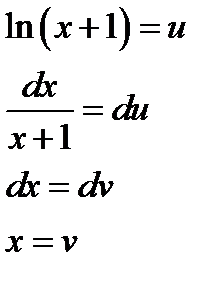
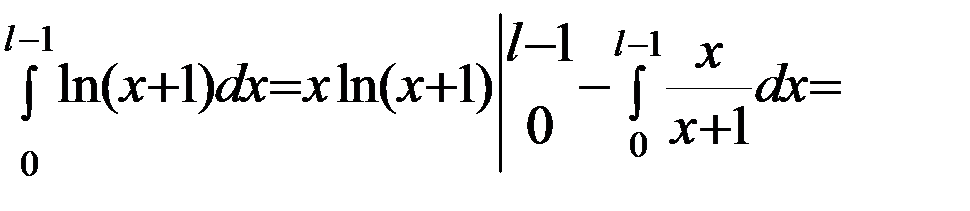
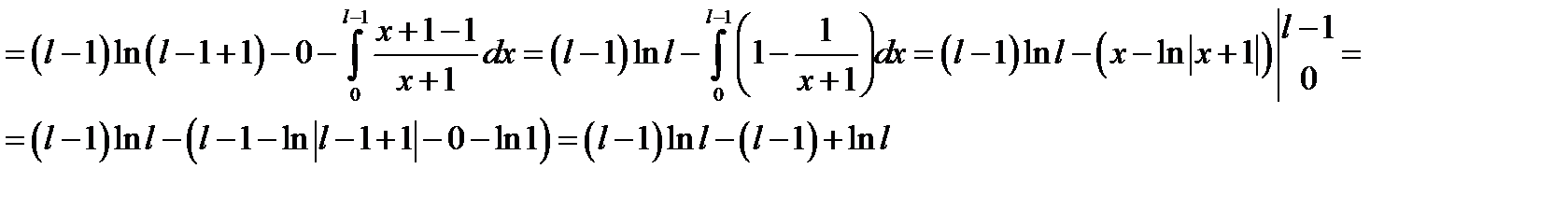 Пример 4.
Пример 4.
Вычислить интеграл 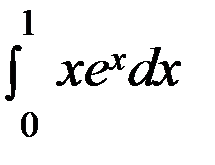 .
.
Решение: Положим 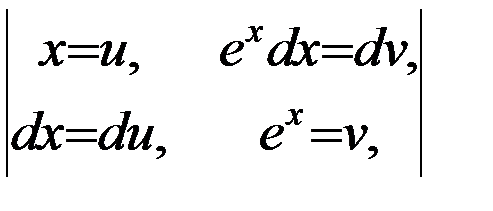 , тогда получим:
, тогда получим:
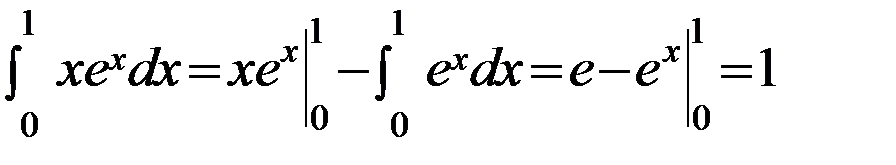 .
.
Пример 4. Вычислить интеграл 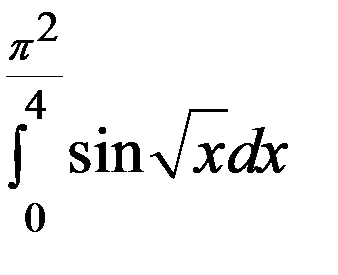 .
.
Решение: Сначала применим подстановку 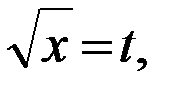
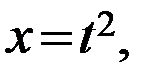
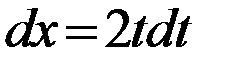 ,
,
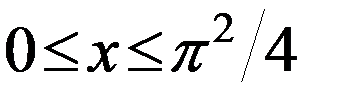 ,
, 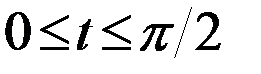 .
.
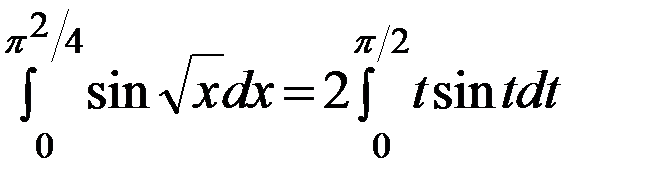 .
.
Последний интеграл будем интегрировать по частям. Положим
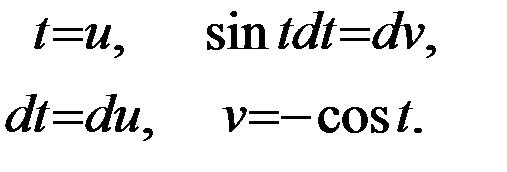
Тогда 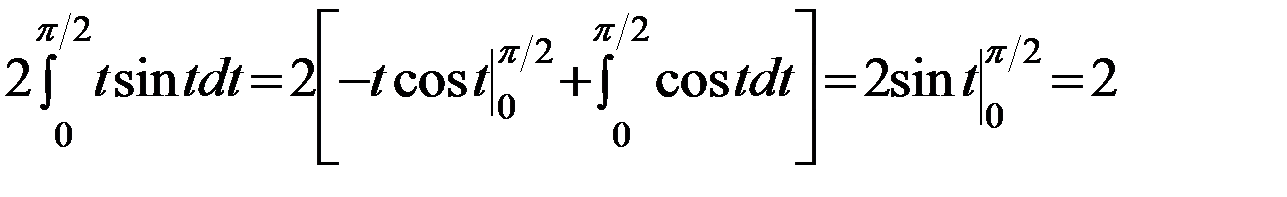 .
.
Пример 5. Вычислить интеграл: 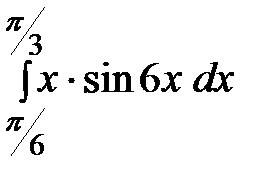
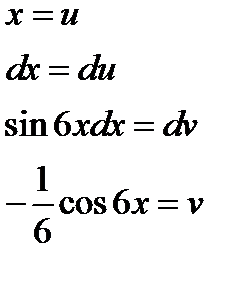
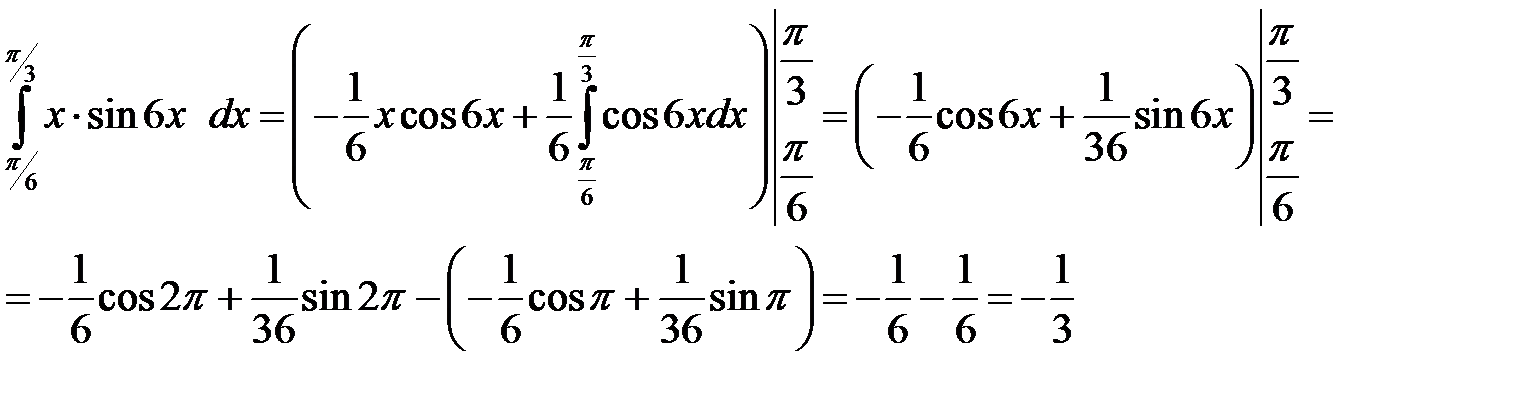
Пример 6. Вычислить интеграл: