Нахождение промежутков монотонности, экстремумов функции
Правило Лопиталя
Задача 1.Вычислить 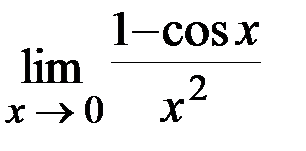 .
.
Решение: 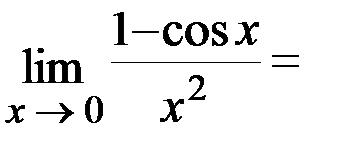
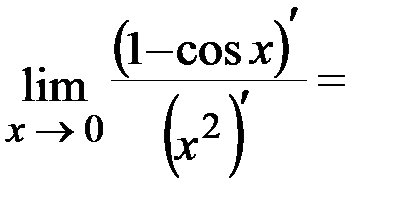
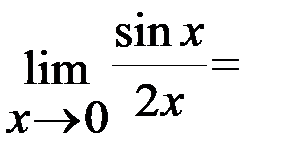
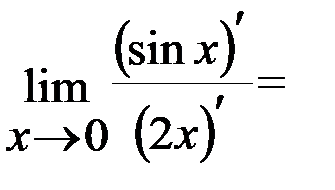
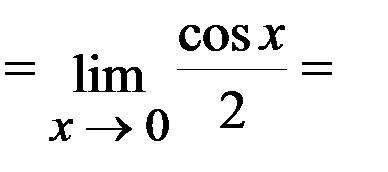
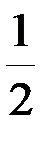 .
.
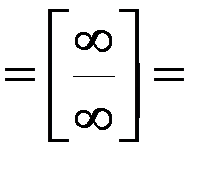
Задача 2.Вычислить 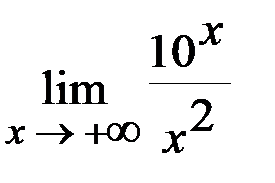 .
.
Решение:
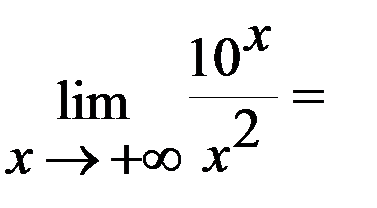
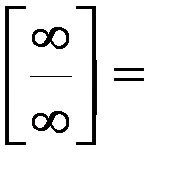
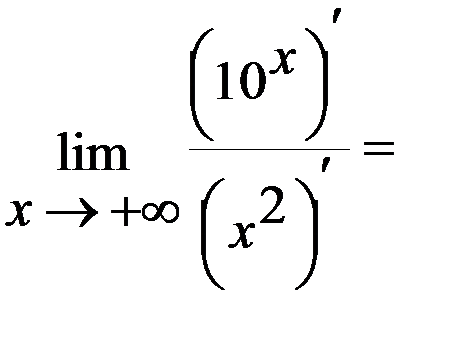
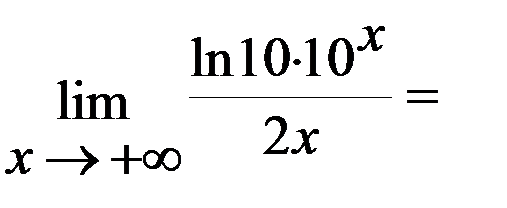
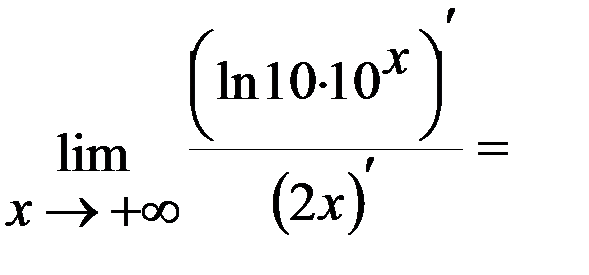
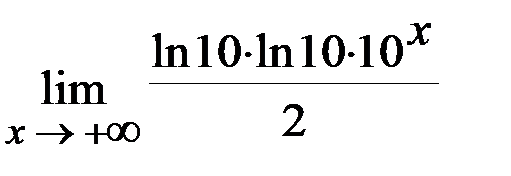
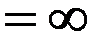 .
.
Задача 3. Вычислить 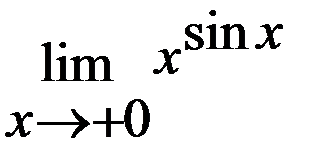 .
.
Решение:
Ясно, что рассматриваемый предел представляет собой неопределенность типа  . Логарифмируем выражение
. Логарифмируем выражение 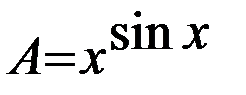 , получаем
, получаем 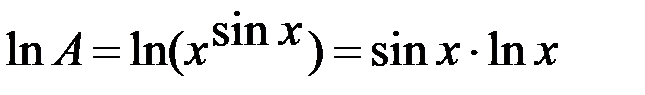 .
.
С учетом последнего равенства находим
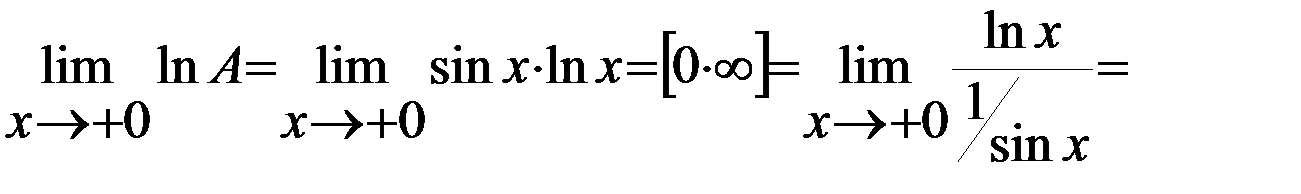
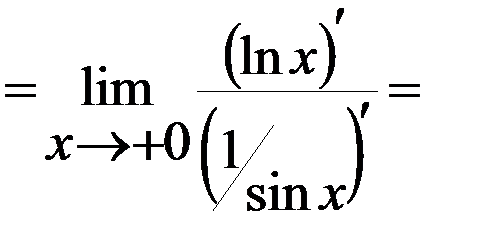
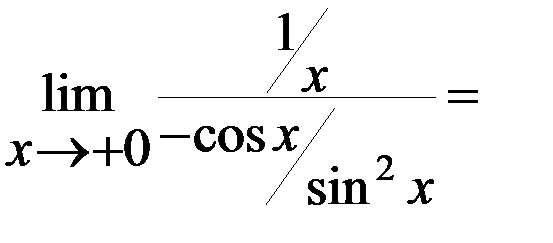
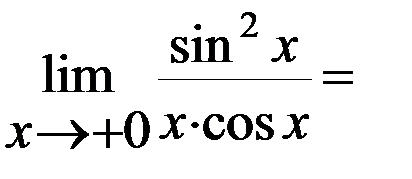
= 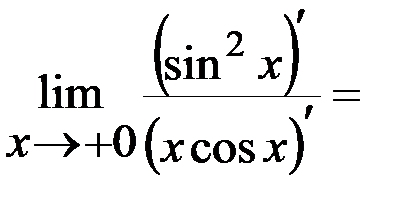
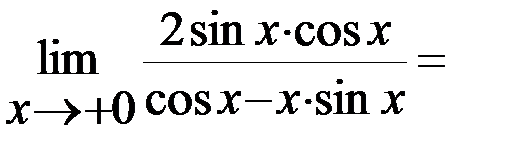 0.
0.
Воспользовавшись непрерывностью функции 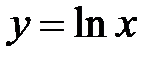 на вcей естественной области определения, получим:
на вcей естественной области определения, получим: 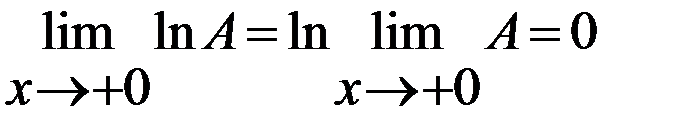 . Отсюда
. Отсюда 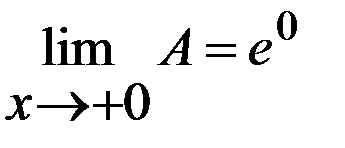 =1.
=1.
Следовательно, 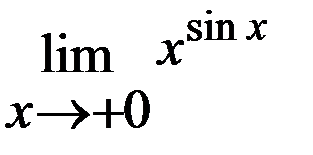 =1.
=1.
Найти значения пределов:
№1
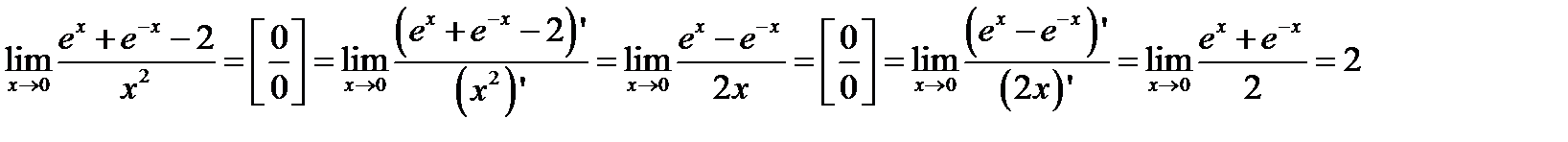
№2 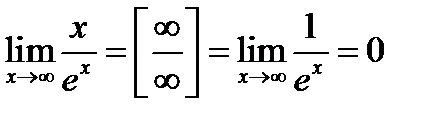
№3. 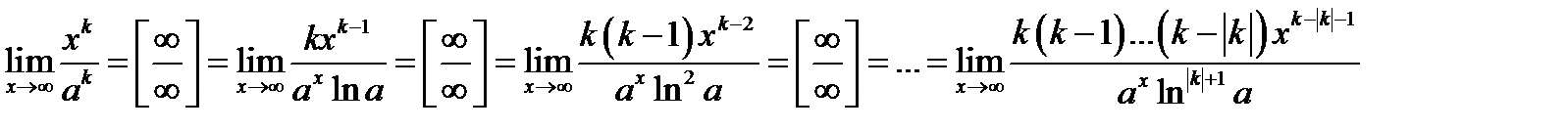
№4. 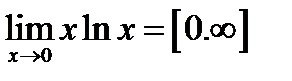 Перепишем данное выражение в виде
Перепишем данное выражение в виде 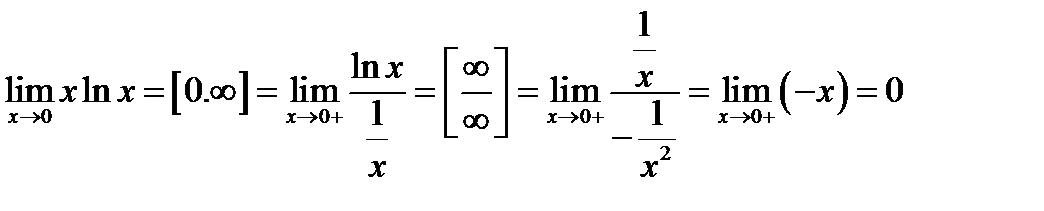 .
.
№5 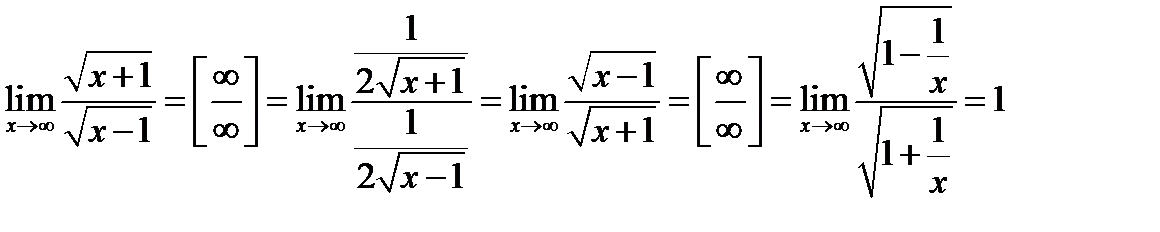 .
.
№6. 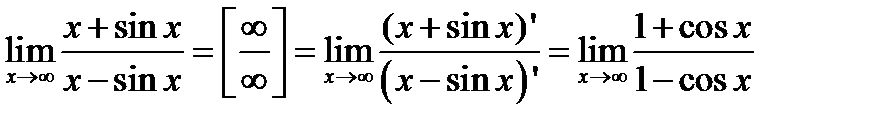 . В этом случае применение правила Лопиталя ошибочно, лучше сделать преобразования
. В этом случае применение правила Лопиталя ошибочно, лучше сделать преобразования 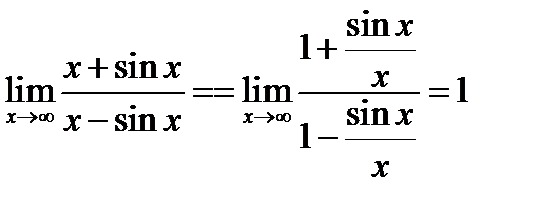 , т.к.
, т.к. 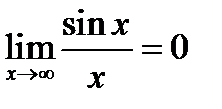
№7. 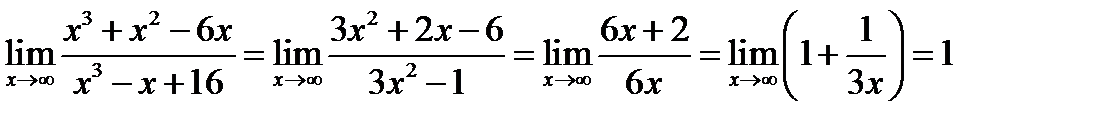 .
.
№8. 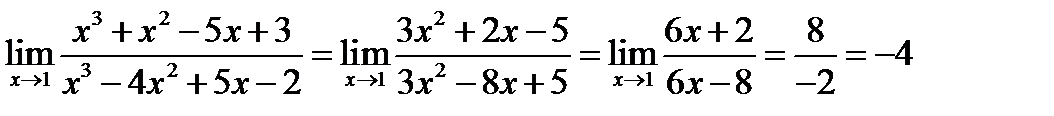 .
.
№9. 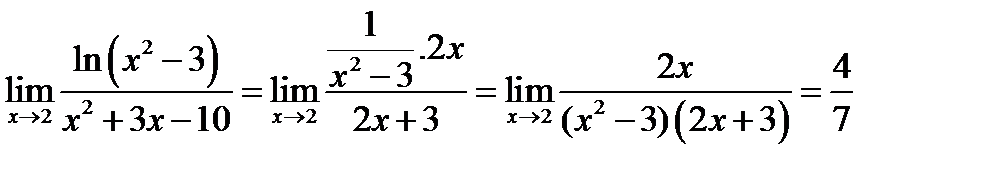 .
.
№10. 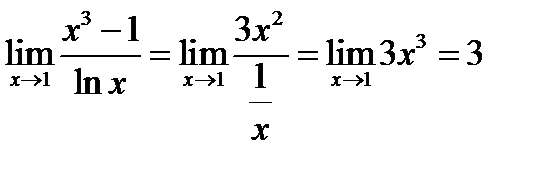 .
.
№11. 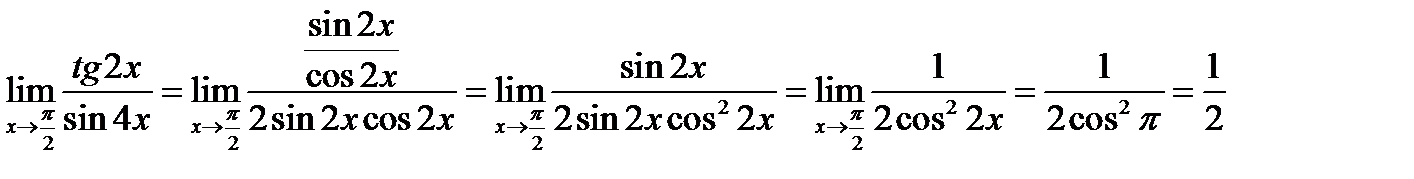
или 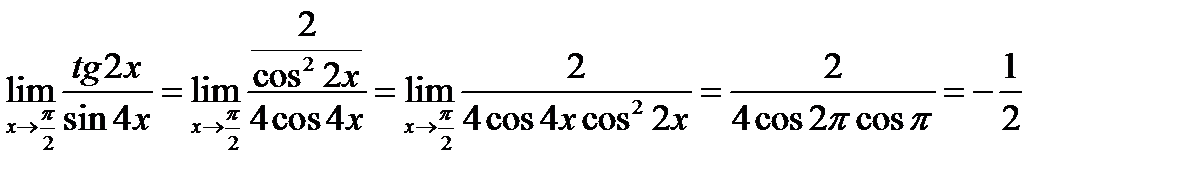 .
.
№12. 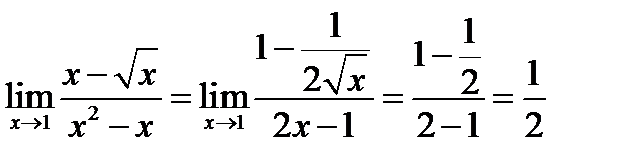 .
.
№13. 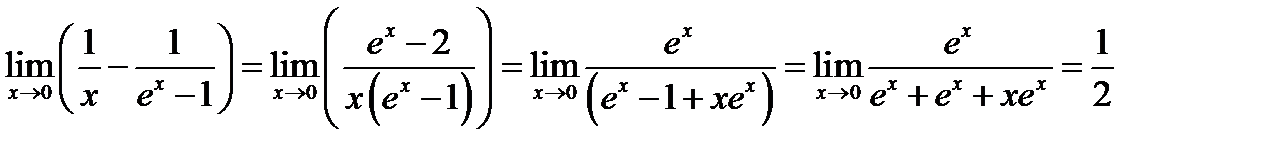 .
.
№14. 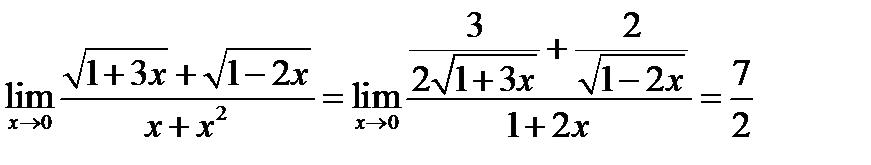 .
.
№15. 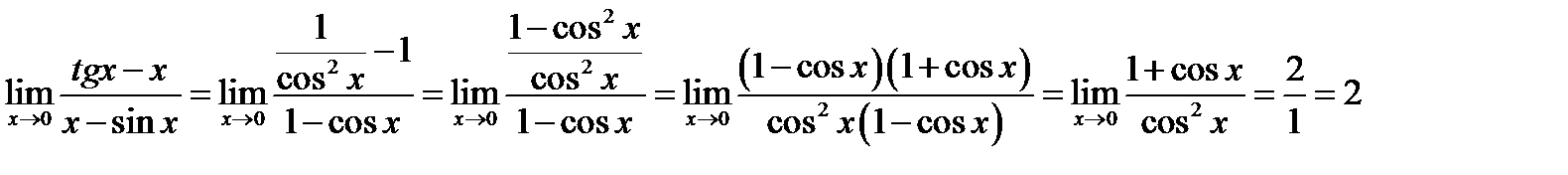 .
.
№ 16. 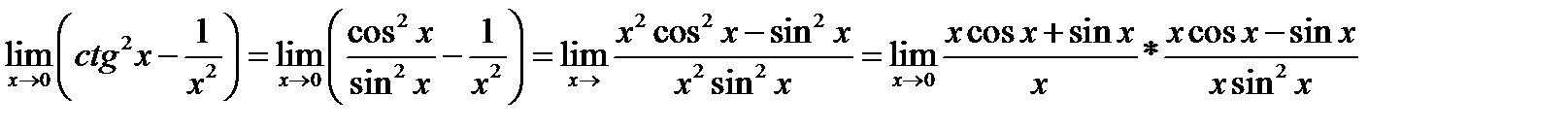
предел первого множителя 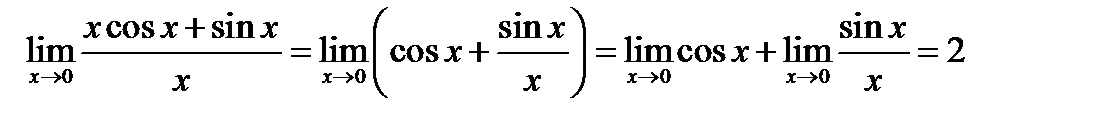
предел второго множителя: 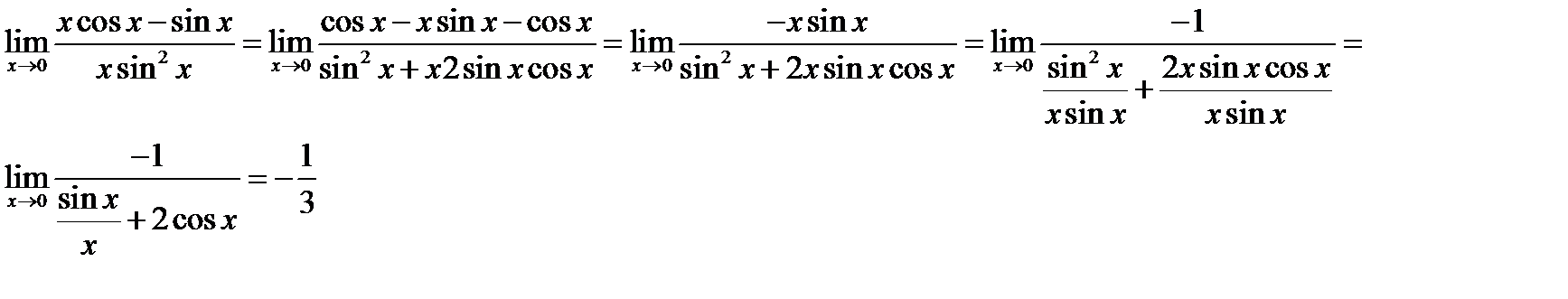 Таким образом, искомый предел равен
Таким образом, искомый предел равен 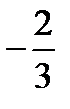 .
.
№17. 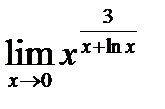 =(логарифмируем заданную функцию, применяем свойство степени, получаем)=
=(логарифмируем заданную функцию, применяем свойство степени, получаем)= 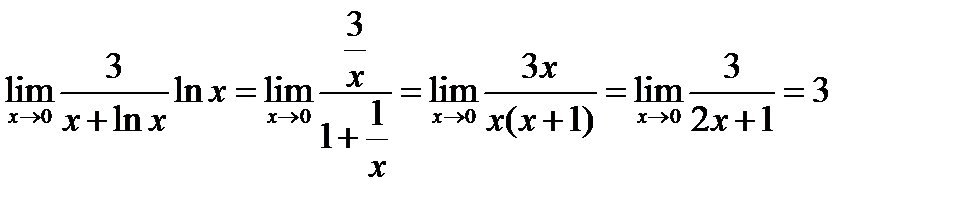 .
.
№18
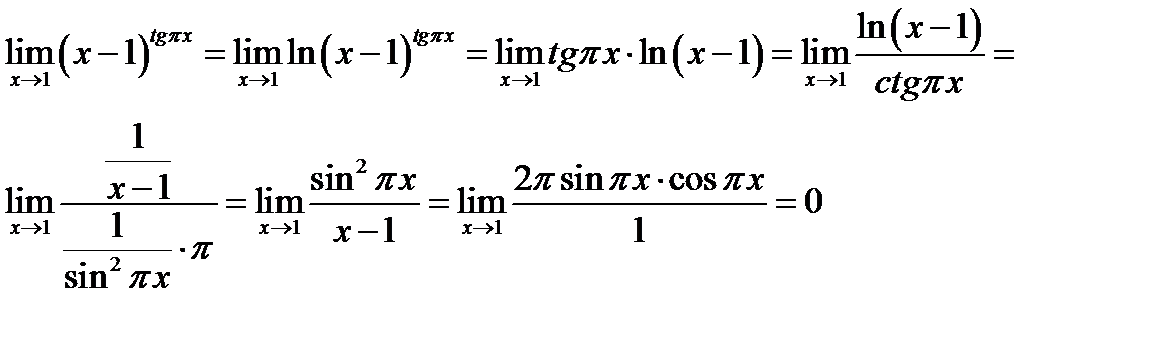
№19. 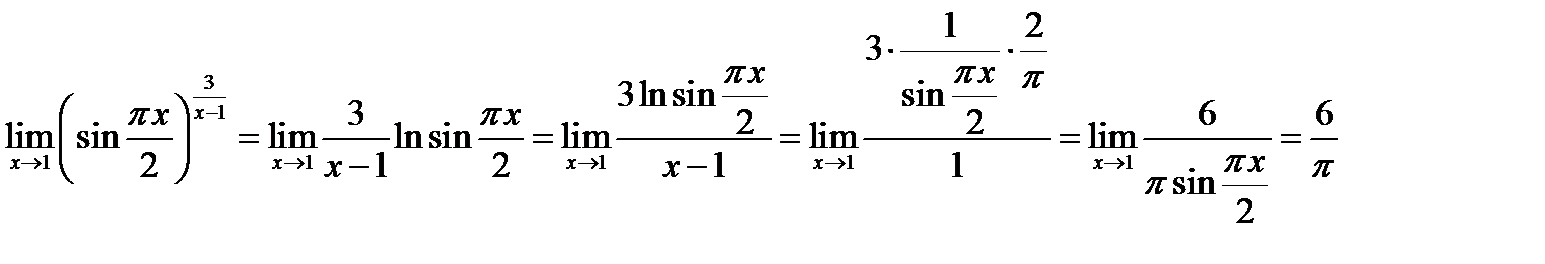
Нахождение промежутков монотонности, экстремумов функции
Пример: Исследовать на максимум и минимум функцию.
а) 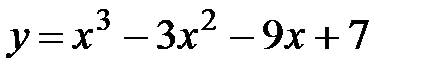 .
.
1. Область определения функции D(y)=R.
2. 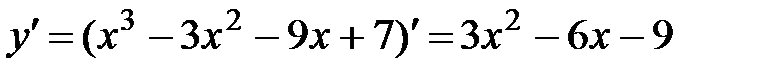 .
.
Критические точки: 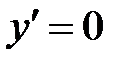 .
. 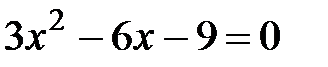 ,
, 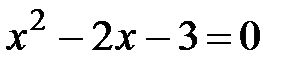 Þ
Þ 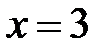 ,
, 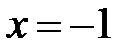 .
.
3. 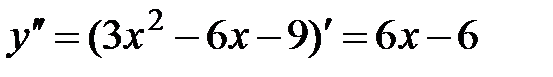 .
.
| x | x=-1 | x=3 |
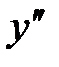 | -12 | |
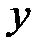 | max y(-1)=12 | min y(3)=-20 |
б) 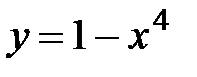 .
.
1. Область определения функции D(y)=R.
2. 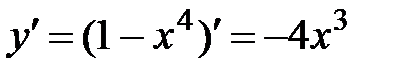 .
.
Критические точки: 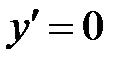 .
. 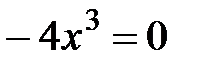 Þ
Þ 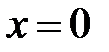 .
.
3. 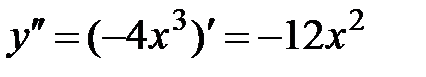 .
.
| x | (-∞;0) | x=0 | (0;+∞) |
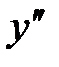 | |||
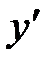 | + | – | |
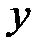 | возрастает | max y(0)=1 | возрастает |
в) Исследовать функцию на монотонность и найти точки экстремума:
а) 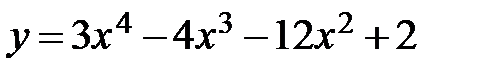 .
.
1. Область определения функции D(y)=R.
2. 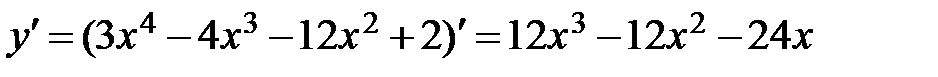 .
.
Критические точки: 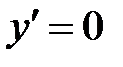 .
. 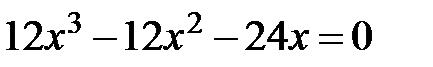 ,
, 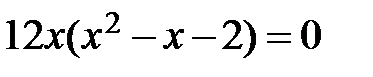 Þ
Þ 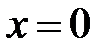 ,
, 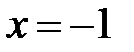 ,
, 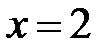 .
.
| x | (-∞;-1) | x=-1 | (-1;0) | x=0 | (0;2) | x=2 | (3;+∞) |
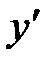 | – | + | – | + | |||
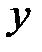 | убывает | min y(-1)=-3 | возрастает | max y(0)=2 | убывает | min y(2)=-30 | возрастает |
б) 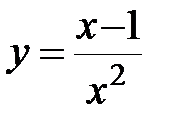 .
.
1. Область определения функции D(y): x¹0.
2. 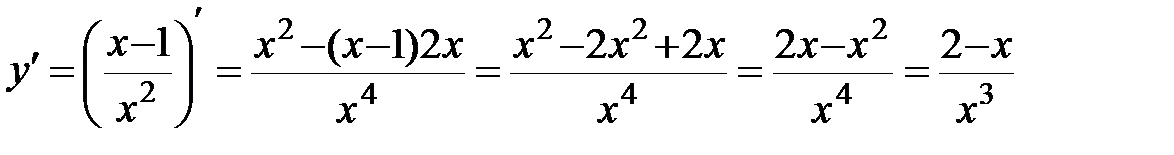 ;
;
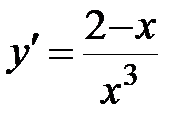 .
.
Критические точки: 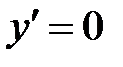 , т.е. числитель равен нулю Þ
, т.е. числитель равен нулю Þ 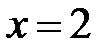 ;
;
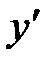 – не существует, т.е. знаменатель равен нулю Þ
– не существует, т.е. знаменатель равен нулю Þ 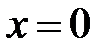 .
.
| x | (-∞;0) | x=0 | (0;2) | x=2 | (2;+∞) |
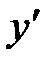 | – | не существует | + | − | |
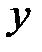 | убывает | не существует | возрастает | max y(2)=0,25 | убывает |
Найти интервалы монотонности функции 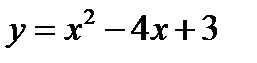
Решение. Имеем 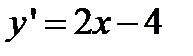 . Очевидно
. Очевидно 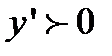 при
при 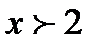 и
и 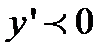 при
при 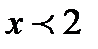 , т.е. функция убывает на интервале
, т.е. функция убывает на интервале 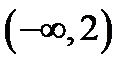 и возрастает на интервале
и возрастает на интервале 
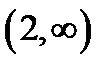 , где .
, где . 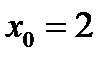 — абсцисса вершины параболы.
— абсцисса вершины параболы.
Заметим, что необходимое условие монотонности более слабое. Если функция возрастает (убывает) на некотором промежутке . 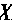 , то можно лишь утверждать, что производная неотрицательна (неположительна) на этом промежутке:
, то можно лишь утверждать, что производная неотрицательна (неположительна) на этом промежутке: 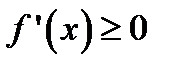 (
( 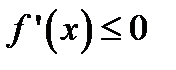 ) т.е. в отдельных точках производная монотонной функции может равняться нулю.
) т.е. в отдельных точках производная монотонной функции может равняться нулю.
Пример. Найти интервалы монотонности функции 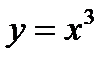
Решение. Найдем производную 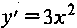 . Очевидно, что
. Очевидно, что 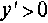 , при
, при 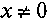 . При
. При 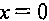 производная обращается в нуль. Функция же монотонно возрастает на всей числовой оси.
производная обращается в нуль. Функция же монотонно возрастает на всей числовой оси.
Исследовать на экстремум функцию 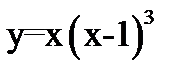
Решение. 1°. Производная функции 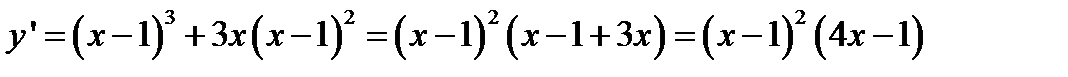
2°. Приравнивая производную к нулю, находим критические
точки функции 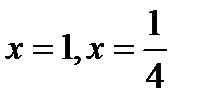 . (Точек, в которых производная не
. (Точек, в которых производная не
существует, у данной функции нет —функция определена на всей числовой оси).
3°.
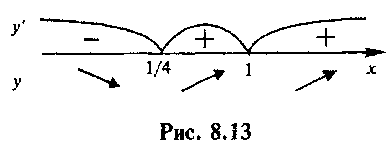
Нанесем критические точки на числовую прямую.
Для определения знака производной слева и справа от критической точки 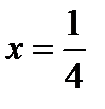 выберем значения, например,
выберем значения, например, 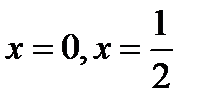 и найдем и
и найдем и 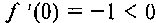
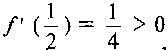 ; следовательно,
; следовательно, 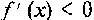 при всех
при всех 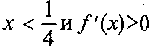
на интервале 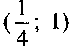 . Аналогично устанавливаем, что
. Аналогично устанавливаем, что 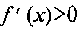 и на интервале
и на интервале 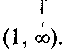
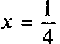 Согласно достаточному условию — точка минимума
Согласно достаточному условию — точка минимума
данной функции. В точке х= 1 экстремума нет.
4°. Находим 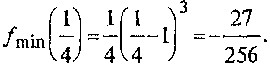 ►
►
Решение задач
1) Найти наибольшее и наименьшее значения функции на отрезке:
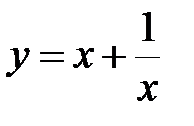 ,
, 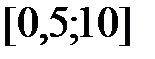 .
.
Решение:
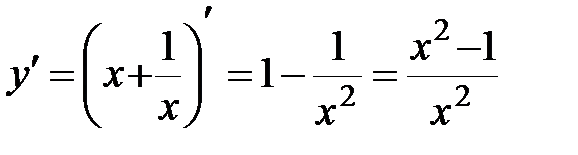 ;
;
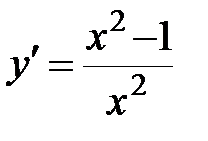 .
.
Критические точки:
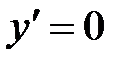 , т.е. числитель равен нулю Þ
, т.е. числитель равен нулю Þ 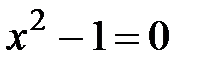 ;
; 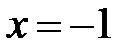 ,
, 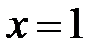 .
.
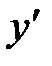 – не существует, т.е. знаменатель равен нулю Þ
– не существует, т.е. знаменатель равен нулю Þ 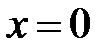 .
.
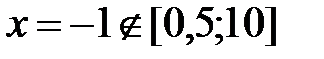 ,
, 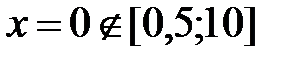 ,
, 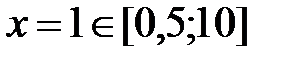 .
.
Найдем значения функции в точке 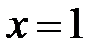 и на концах отрезка:
и на концах отрезка:
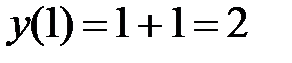 ;
;
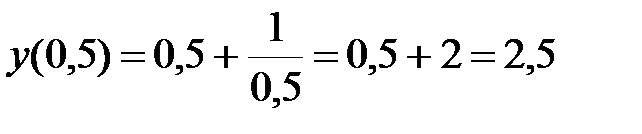 ;
;
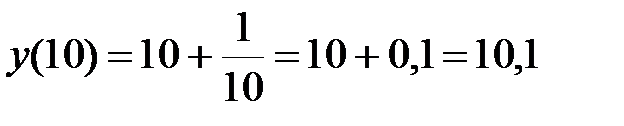 .
.
Наибольшее значение функции равно 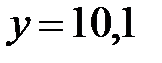 при
при 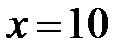 ;
;
Наименьшее значение функции равно 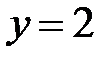 при
при 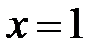 .
.
Пример. Исследовать функцию 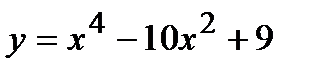 и построить ее график.
и построить ее график.
Решение.
1) Функция определена и непрерывна на всей оси. Итак, 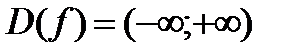 .
.
2) Найдем точки пересечения с осями координат.
а) с осью ОХ: 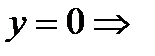
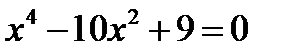
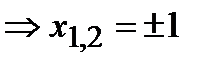 ,
, 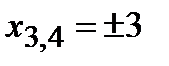 .
.
Следовательно, точки пересечения с осью ОХ - 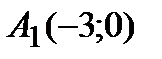 ,
, 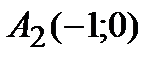 ,
, 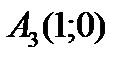 ,
, 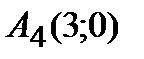 ;
;
б) с осью ОY: 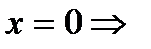
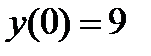 .
.
Следовательно, точка пересечения с осью ОY - 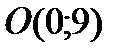 .
.
3) Функция четная, так как 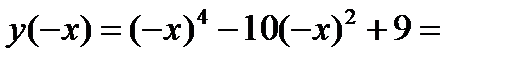
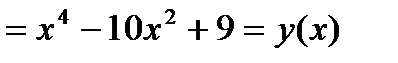 (поэтому ее график будет симметричен относительно оси OY).
(поэтому ее график будет симметричен относительно оси OY).
Функция непериодическая.
4) С помощью первой производной найдем промежутки возрастания и убывания функции.
Имеем 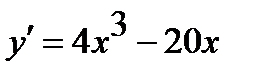 =0. Следовательно, точки
=0. Следовательно, точки 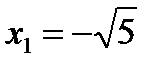 ,
, 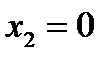 ,
, 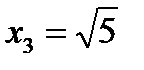 будут подозрительными на экстремум. Разбиваем всю область определения на промежутки
будут подозрительными на экстремум. Разбиваем всю область определения на промежутки 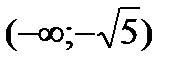 ,
, 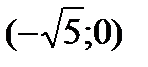 ,
, 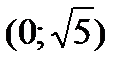 ,
, 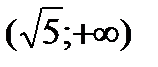 и исследуем функцию для
и исследуем функцию для 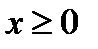 . Информация о поведении функции на интервале
. Информация о поведении функции на интервале 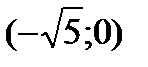 необходима для анализа функции в точке
необходима для анализа функции в точке 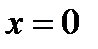 . По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:
. По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:
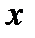 | 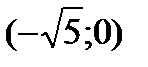 | 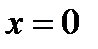 | 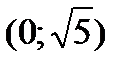 | 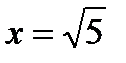 | 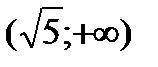 |
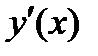 | 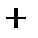 | 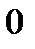 | 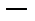 | 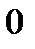 | 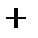 |
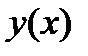 | Возрастает | 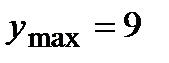 | Убывает | 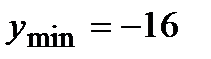 | Возрастает |
5) Чтобы исследовать функцию на выпуклость, найдем вторую производную: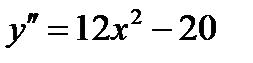 .Находим точки, в которых
.Находим точки, в которых 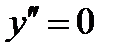 или
или 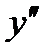 не существует.
не существует.
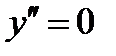 при
при 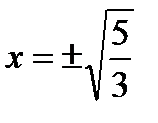 .
.
Исследуем знак второй производной на промежутках 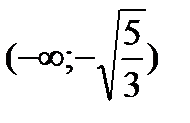 ,
, 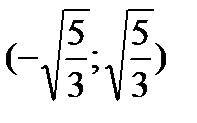 ,
, 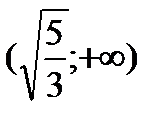 и результаты исследований представим в таблице:
и результаты исследований представим в таблице:
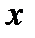 | 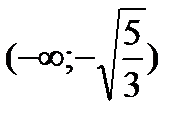 | 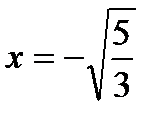 | 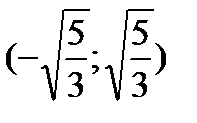 | 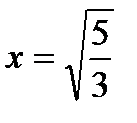 | 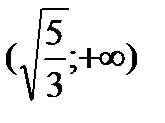 |
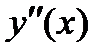 | 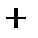 | 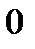 | 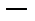 | 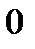 | 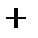 |
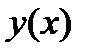 | Выпукла | Перегиб | Вогнута | Перегиб | Выпукла |
6) Вертикальных асимптот нет, поскольку область определения функции – вся числовая ось.
Найдем наклонную асимптоту 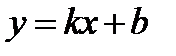 :
:
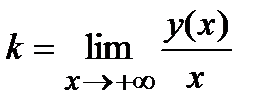 =
= 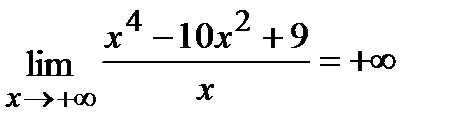 .
.
Следовательно, наклонных асимптот нет.
7) На основе проведенного исследования функции строим ее график (рис.1).
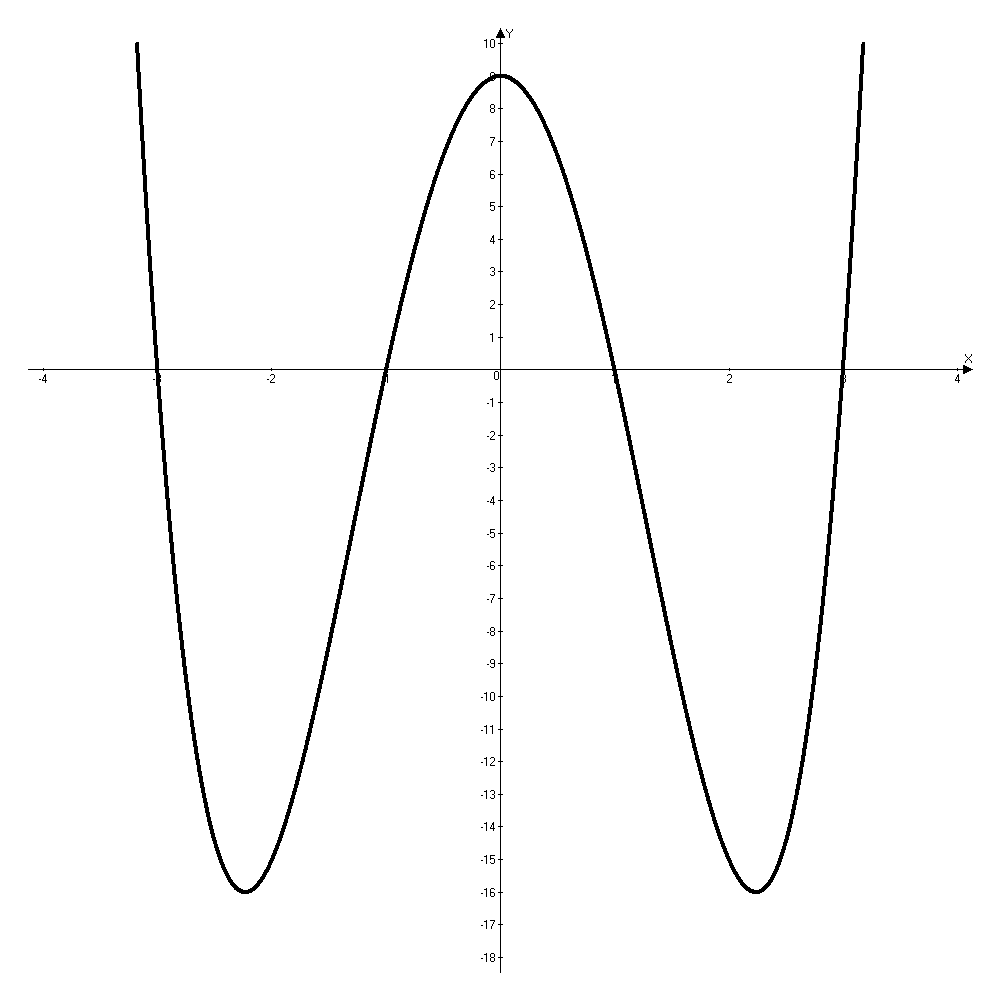
Рис. 1
Пример. Исследовать функцию 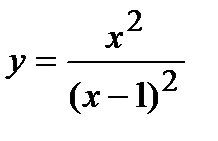 и построить ее график.
и построить ее график.
Решение.
1) Функция определена и непрерывна на всей оси, кроме точки 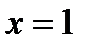 . Итак,
. Итак,  .
.
2) Найдем точки пересечения с осями координат.
а) с осью ОХ: 
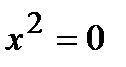
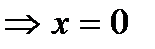 .
.
Следовательно, точка пересечения с осью ОХ - 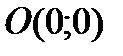 .
.
б) с осью ОY: 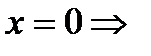
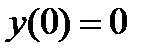 .
.
Следовательно, точка пересечения с осью ОY - 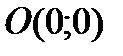 .
.
3) Функция общего вида, так как 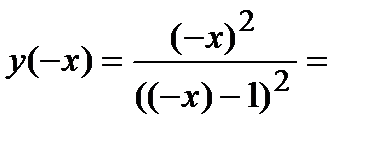
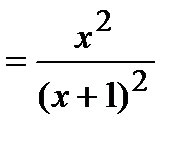 .
.
Функция непериодическая.
4) С помощью первой производной найдем промежутки возрастания и убывания функции.
Имеем 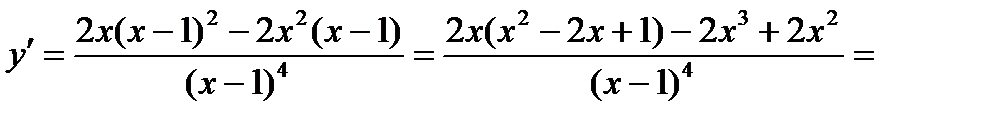
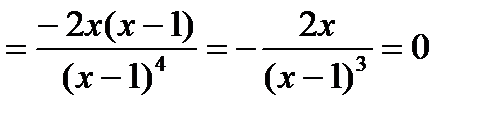 .
.
Следовательно, точка 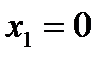 будет подозрительной на экстремум. Точка
будет подозрительной на экстремум. Точка 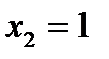 , в которой производная не существует, но в этой точке не существует и функция. Разбиваем всю область определения на промежутки
, в которой производная не существует, но в этой точке не существует и функция. Разбиваем всю область определения на промежутки 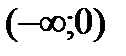 ,
, 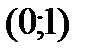 ,
, 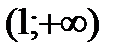 и исследуем функцию на указанных интервалах. По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:
и исследуем функцию на указанных интервалах. По знаку производной определяем монотонность функции на каждом промежутке. Результаты исследований заносим в таблицу:
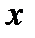 | 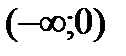 |  | 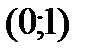 | 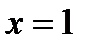 | 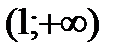 |
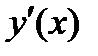 | 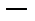 | 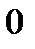 | 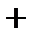 | нет | 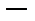 |
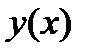 | Убывает | 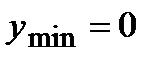 | Возрастает | нет | Убывает |
5) Чтобы исследовать функцию на выпуклость, найдем вторую производную:
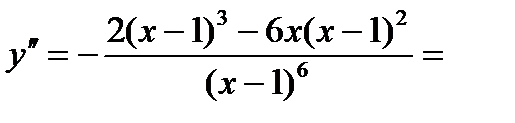
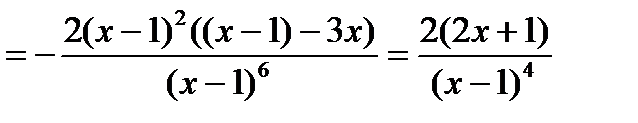 .
.
Находим точки, в которых 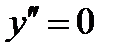 или
или 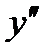 не существует:
не существует: 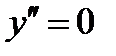 при
при 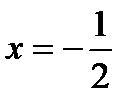 , не существует при
, не существует при 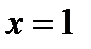 .Исследуем знак второй производной на промежутках
.Исследуем знак второй производной на промежутках 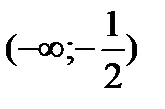 ,
, 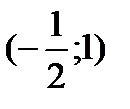 ,
, 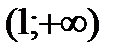 и результаты исследований представим в таблице:
и результаты исследований представим в таблице:
 | 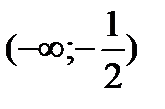 | 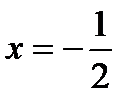 | 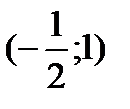 | 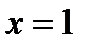 | 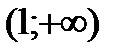 |
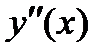 | 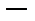 |  | 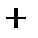 | нет | 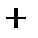 |
 | Вогнута | Перегиб | Выпукла | нет | Выпукла |
6) Найдем вертикальные асимптоты:
Исследуем поведение функции в окрестности точки 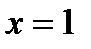 :
:
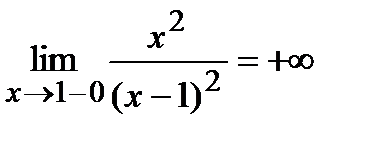 ;
; 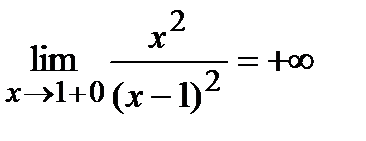 .
.
Пределы не конечны, следовательно, вертикальная асимптота имеет вид: 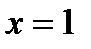 .
.
Найдем наклонную асимптоту 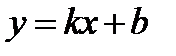 :
:
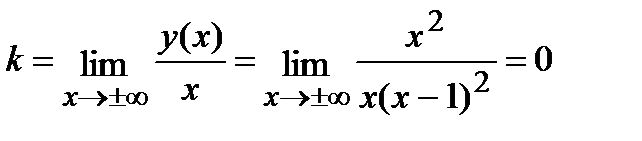 ;
;
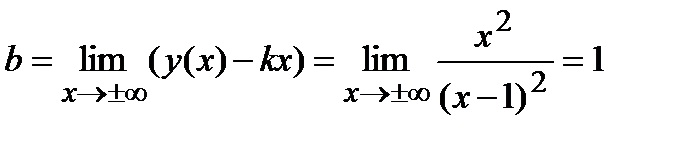 .
.
Следовательно, наклонная асимптота: 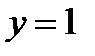 .
.
7) На основе проведенного исследования функции строим ее график (рис.2).
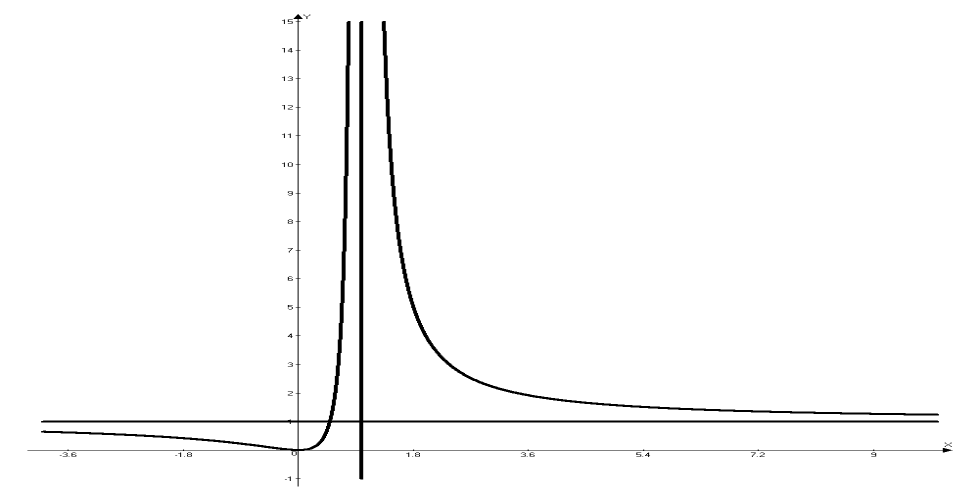
Рис. 2
Замена переменных
1) 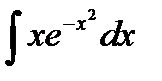
Положим 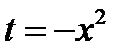 . Продифференцируем обе части полученного равенства
. Продифференцируем обе части полученного равенства 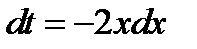 ;
; 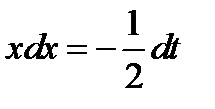
Тогда 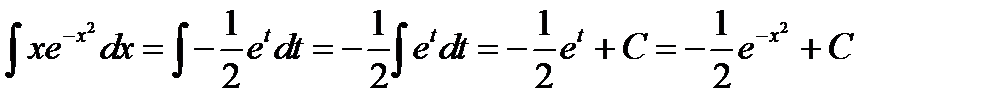
2) 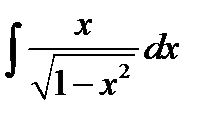 . Положим
. Положим 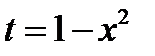 . Продифференцируем обе части полученного равенства
. Продифференцируем обе части полученного равенства 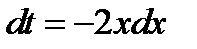 ;
; 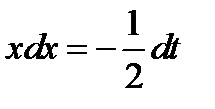
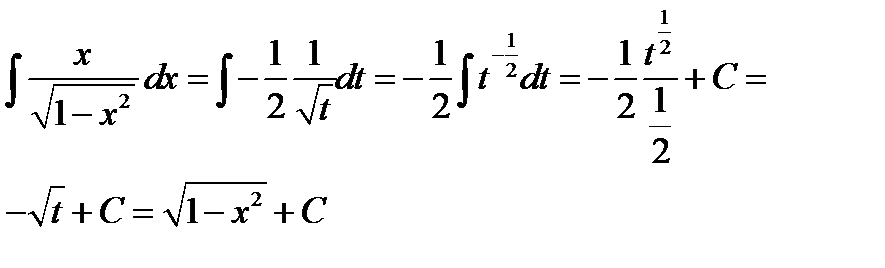
3) 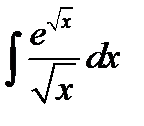 Положим
Положим 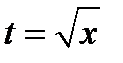 . Продифференцируем обе части полученного равенства
. Продифференцируем обе части полученного равенства 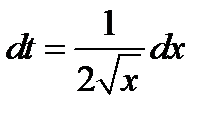 ;
; 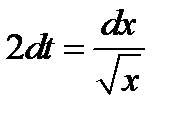 ;
;
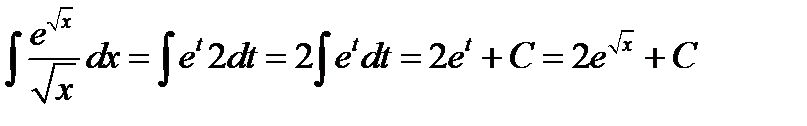
4) 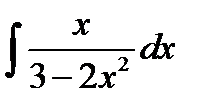 ; Положим
; Положим 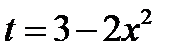 . Продифференцируем обе части полученного равенства
. Продифференцируем обе части полученного равенства 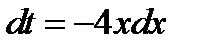 ;
; 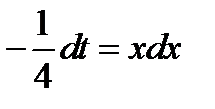
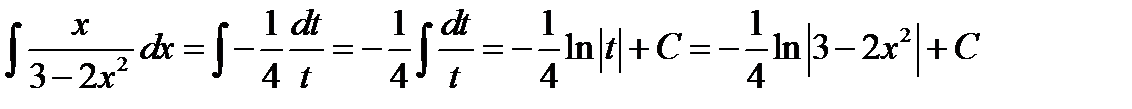
5) 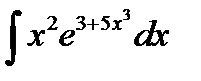 . Положим
. Положим 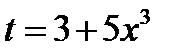 . Продифференцируем обе части полученного равенства
. Продифференцируем обе части полученного равенства 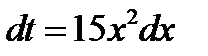 ;
; 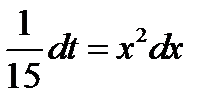
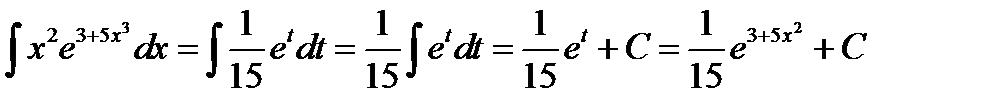
6) 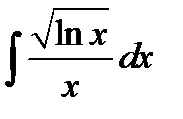 . Положим
. Положим 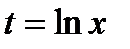 . Продифференцируем обе части полученного равенства
. Продифференцируем обе части полученного равенства 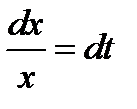
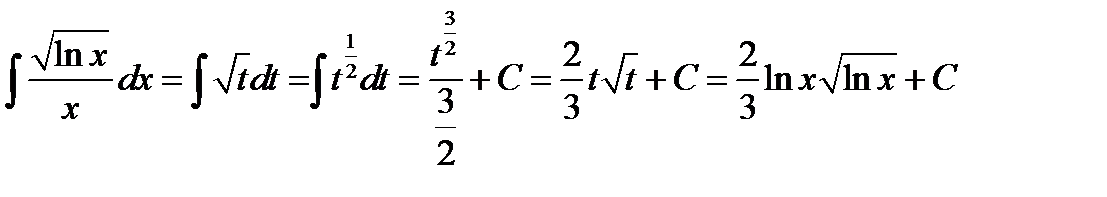 ;
;
7) 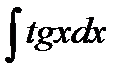
Так как 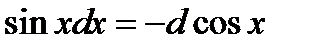 , то
, то 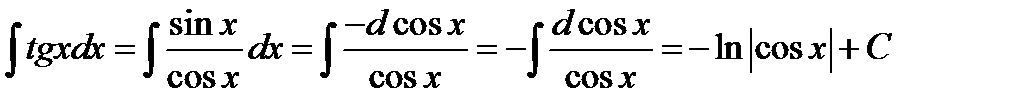
или:
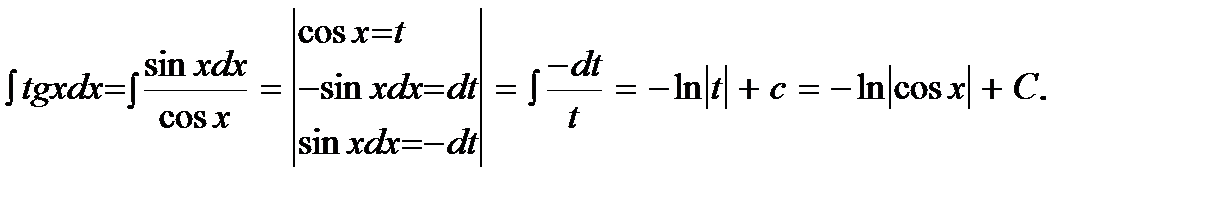
8) 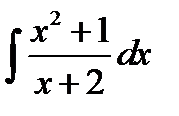
Положим 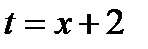 . Тогда
. Тогда 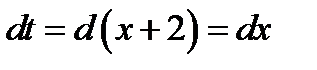
Так как 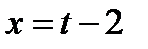 , то
, то
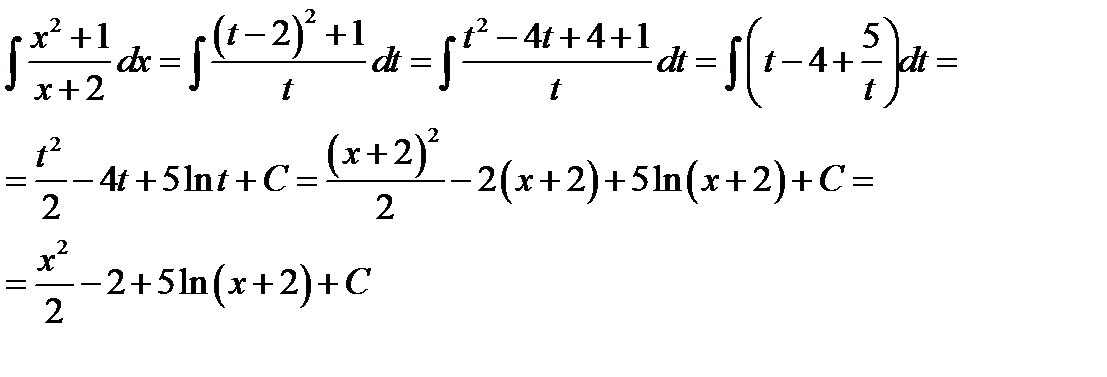
9) 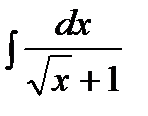 =
= 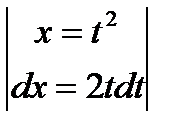 =
= 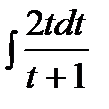 =
= 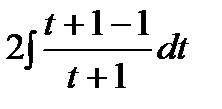 =
= 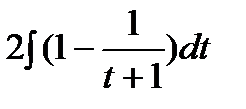 =
= 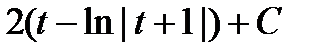 =
= 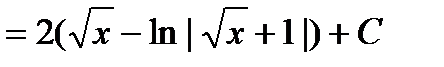 .
.
10) 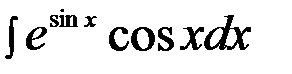 =
= 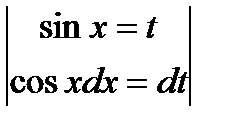 =
= 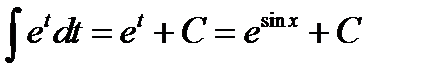
11) 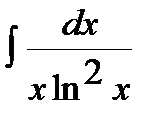 .
.
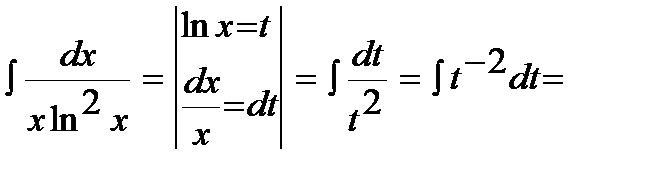
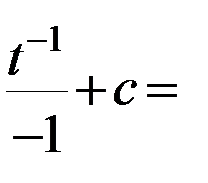
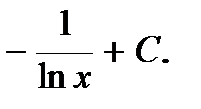
12) 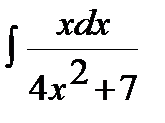 .
.
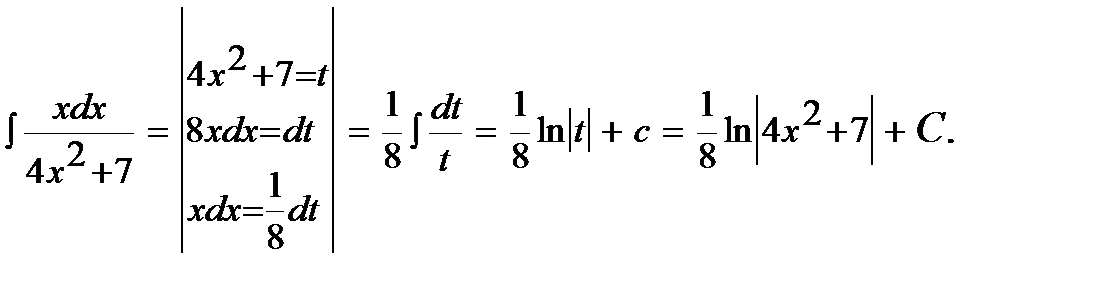
Определенный интеграл
1.Используя формулу Ньютона-Лейбница, вычислить интегралы:
1). 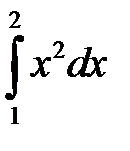
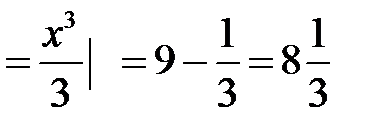

2). 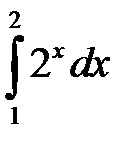 =
= 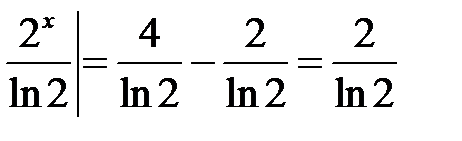
3). 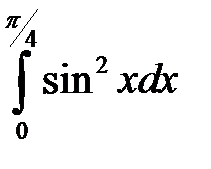
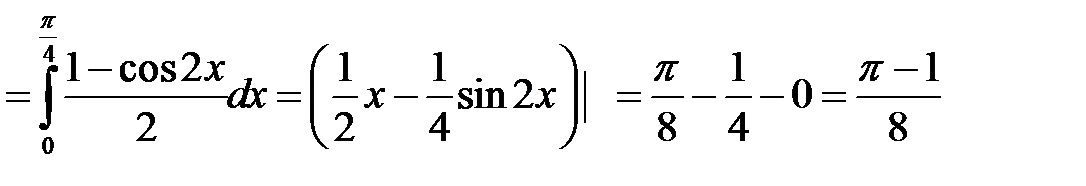
4) 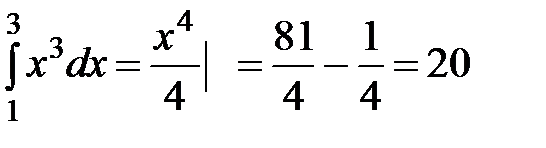
5) 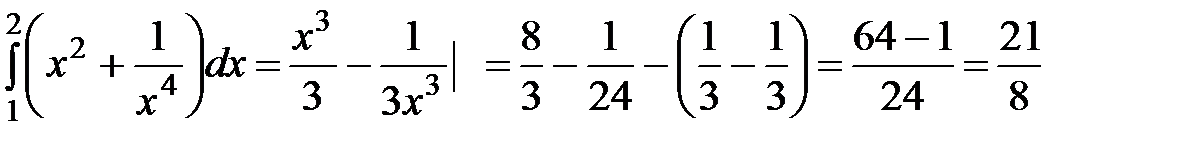
6) 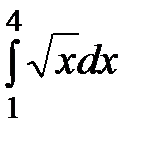
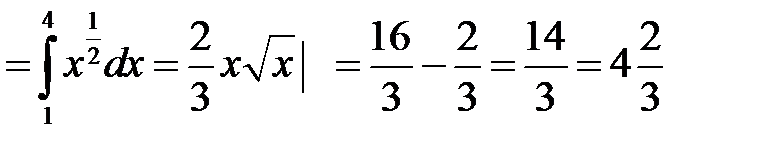
7) 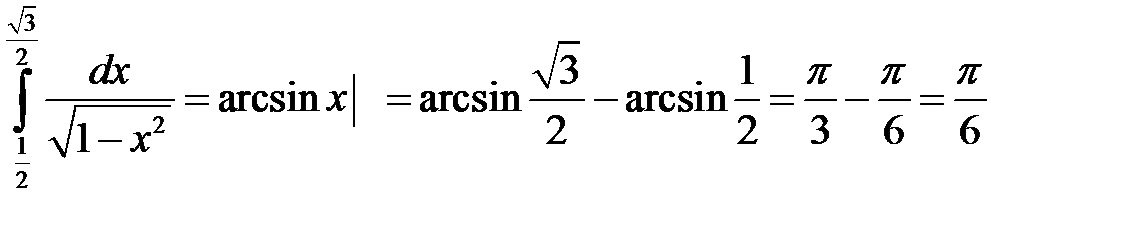
8) 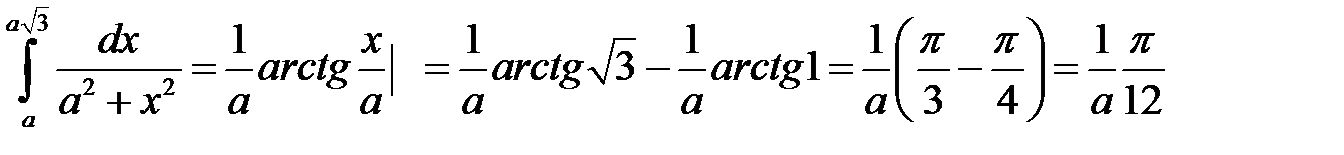
9) 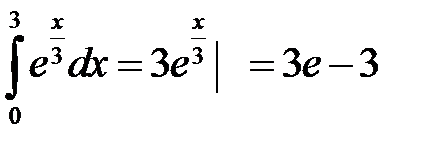

10) 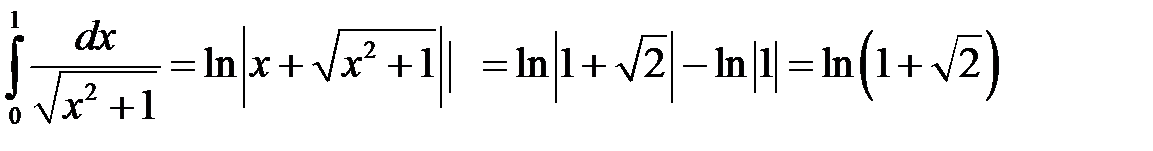

11) 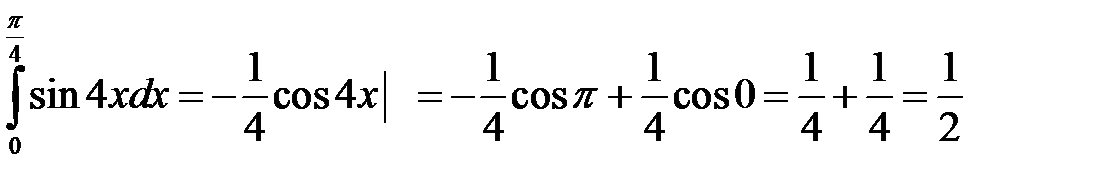
12) 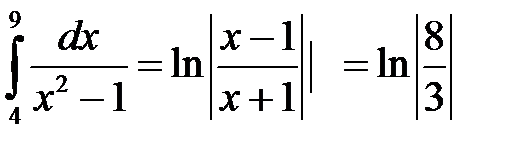
13) 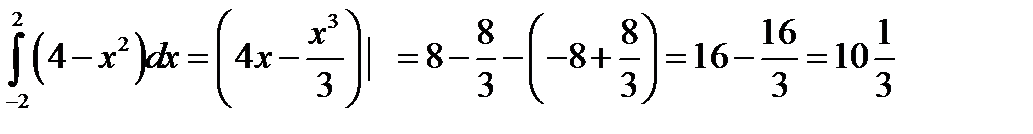
14) 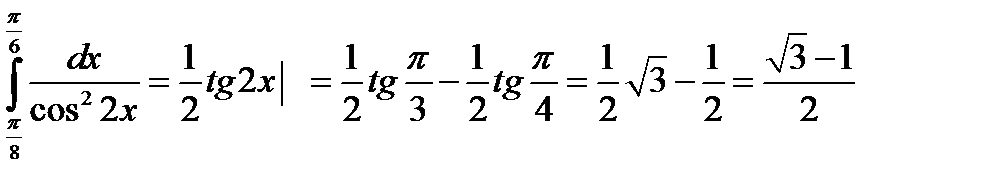
15) 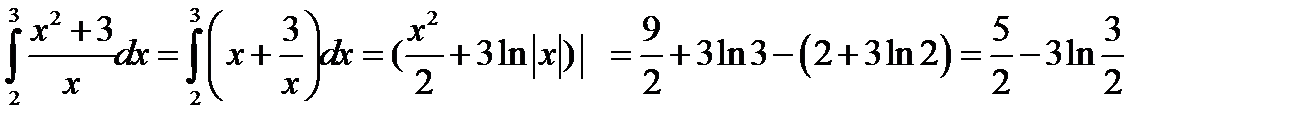
Частные производные.
Задача 1.Найти частные производные от функций:
а) 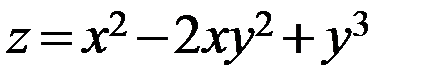 .
.
Решение. Частную производную 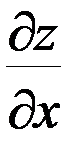 находим как производную функции
находим как производную функции 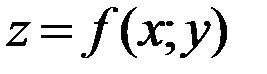 по аргументу
по аргументу 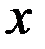 в предположении, что
в предположении, что 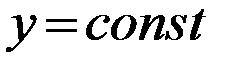 . Поэтому,
. Поэтому,
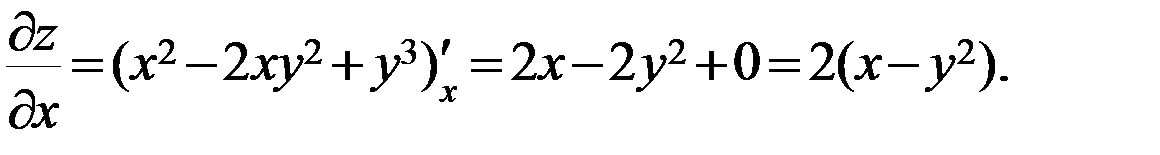
Аналогично,
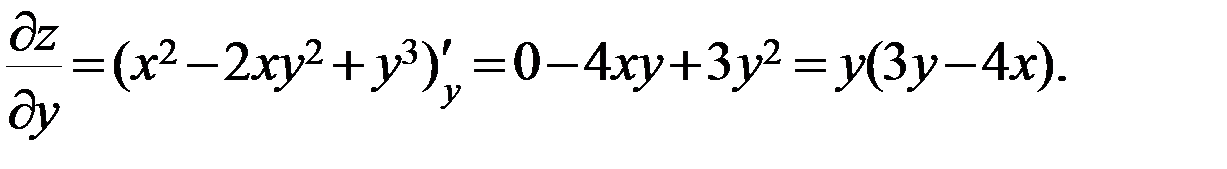
б) 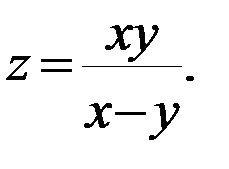
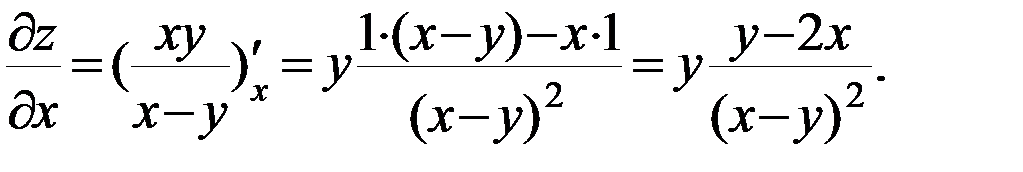
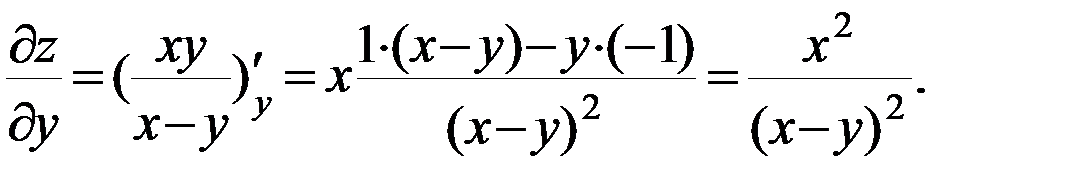
в) 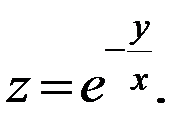
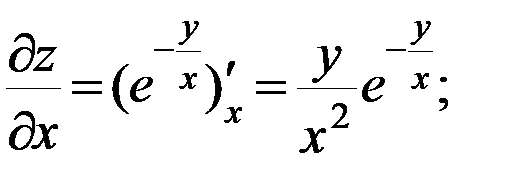
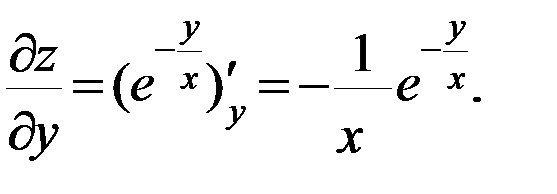
г) 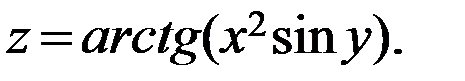
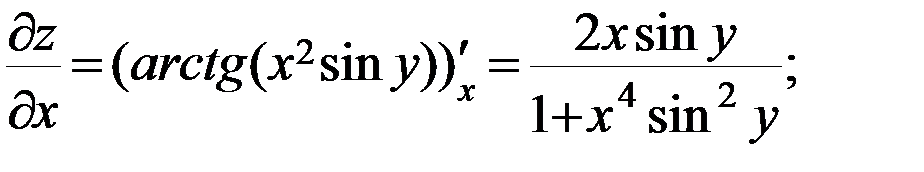
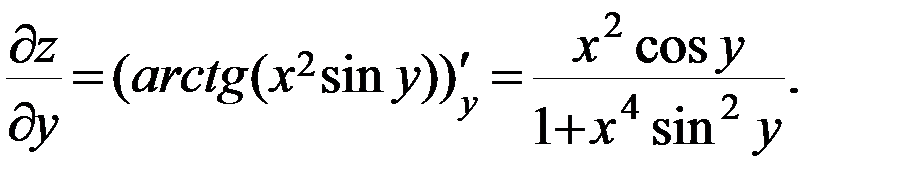
Пример 2
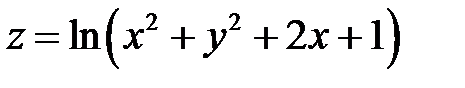 . Показать, что
. Показать, что 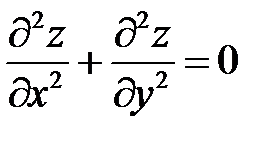 .
.
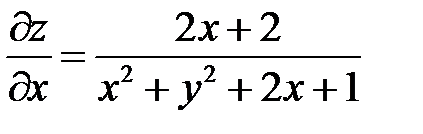
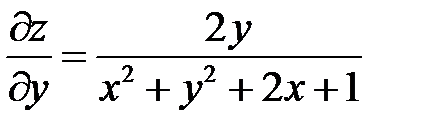
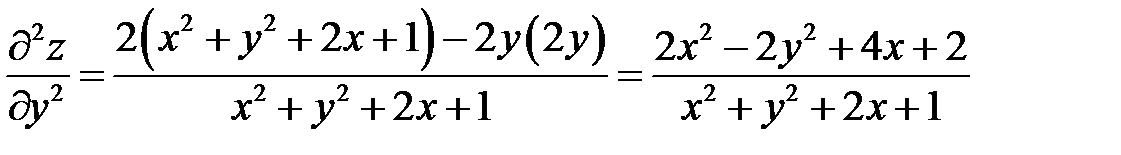
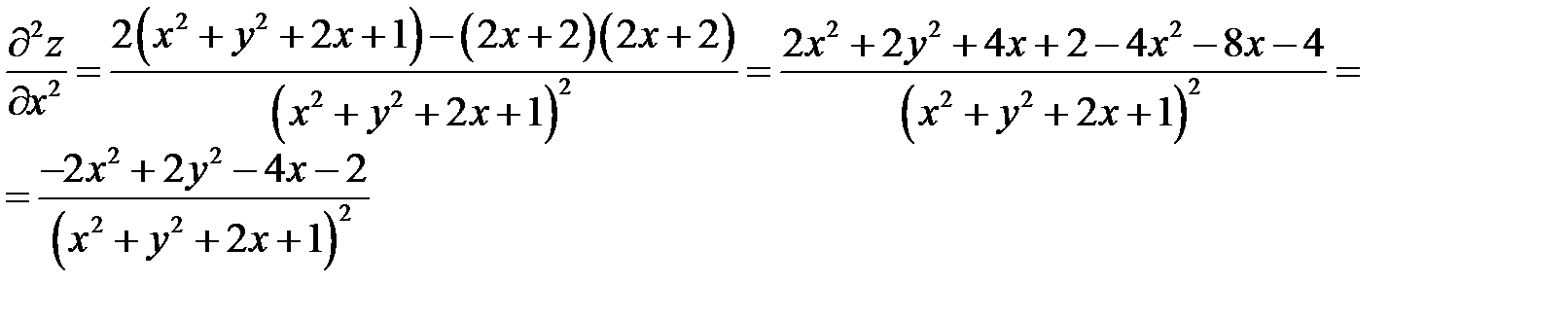
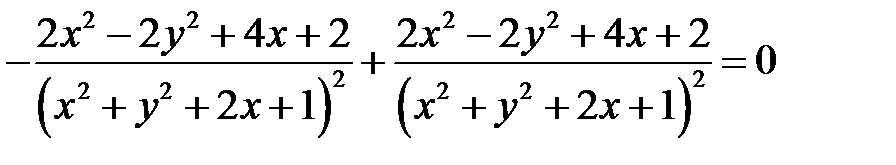
Пример 3
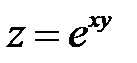 . Показать, что
. Показать, что 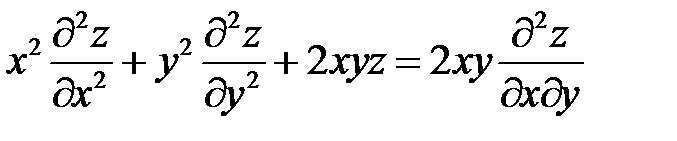 .
.
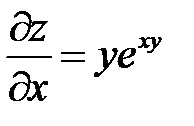
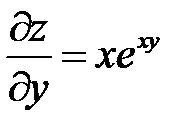
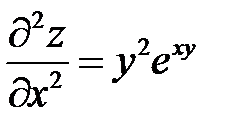
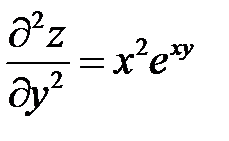
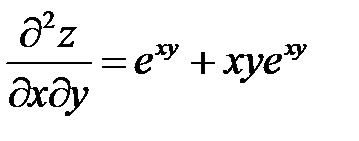
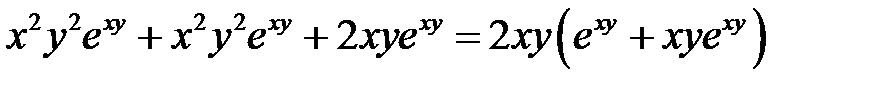
Экстремум функции
Дана функция 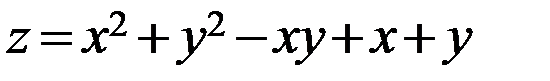 .
.
а) исследовать функцию на экстремум;
Решение. а) Найдем стационарные точки функции из системы уравнений: 
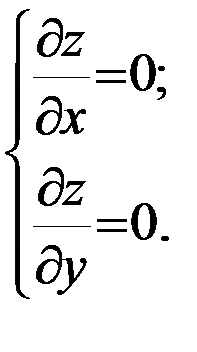
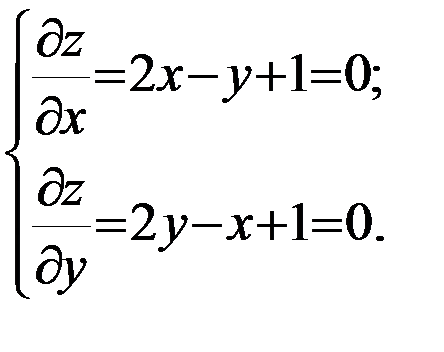
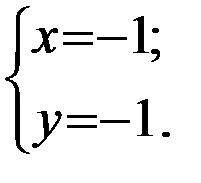 Следовательно,
Следовательно,
Точка 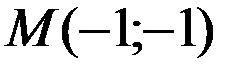 - стационарная точка функции. Вычислим значения частных производных второго порядка в точке
- стационарная точка функции. Вычислим значения частных производных второго порядка в точке 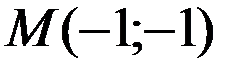 .
.
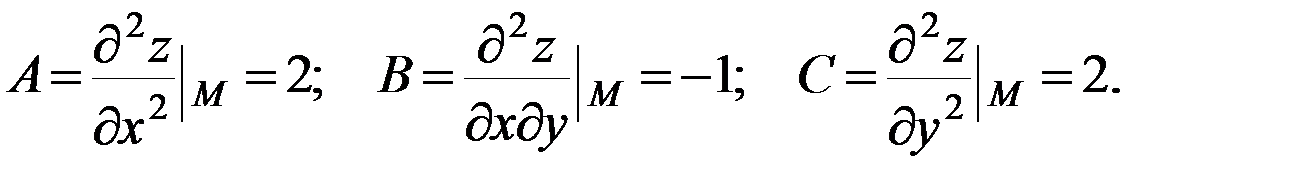
Составим дискриминант 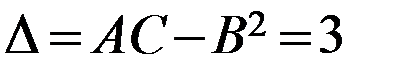 . Так как
. Так как 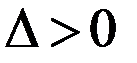 , то экстремум есть, так как
, то экстремум есть, так как 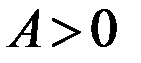 , то
, то 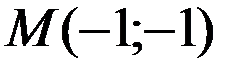 - точка минимума.
- точка минимума.
Решение.
1.Для решение задачи воспользуемся формулой для нахождения производной от функции 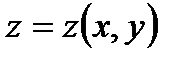 в заданной точке
в заданной точке 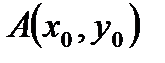 по направлению вектора
по направлению вектора 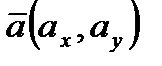 :
:
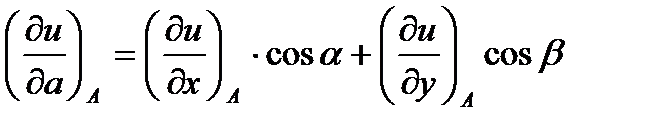 ,
,
где 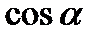 ,
, 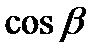 - направляющие косинусы вектора
- направляющие косинусы вектора 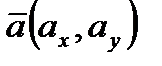 , которые вычисляются по формулам:
, которые вычисляются по формулам: 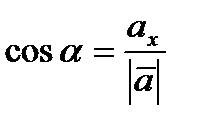 ,
, 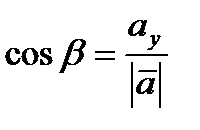 .
.
По условиям задачи вектор 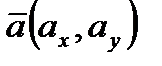 имеет координаты
имеет координаты 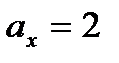 ,
, 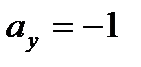 . Тогда его длина равна:
. Тогда его длина равна: 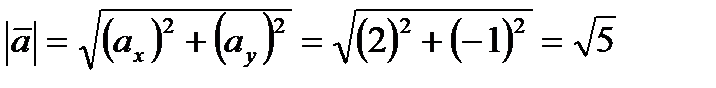 .
.
Следовательно, для направляющих косинусов вектора получим следующие значения: 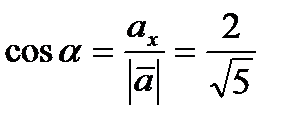 ,
, 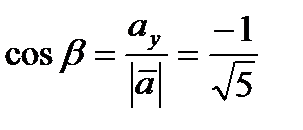 .
.
Для решения задачи необходимо найти все частные производные первого порядка от функции 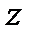 :
:
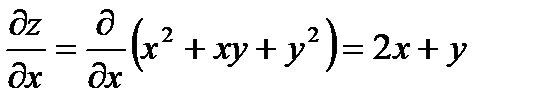
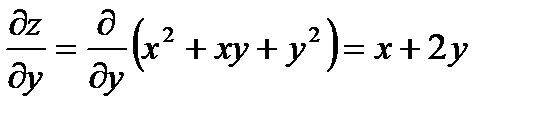
Вычислим значения этих частных производных первого порядка в точке 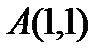
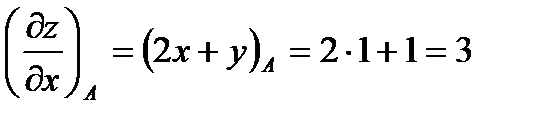
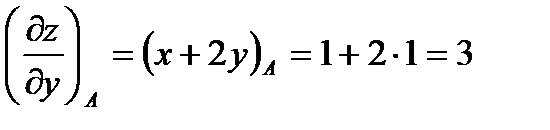
В заключении подставим полученные значения для направляющих косинусов вектора 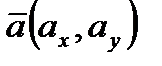 и значения частных производных первого порядка от функции z в точке
и значения частных производных первого порядка от функции z в точке 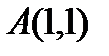 в формулу производной по направлению в заданной точке:
в формулу производной по направлению в заданной точке:
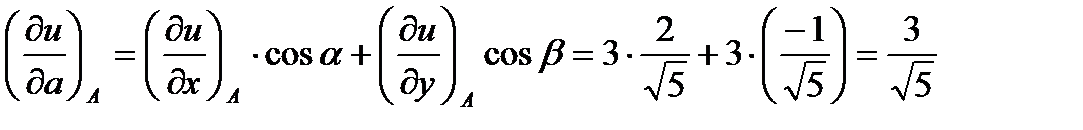
2. 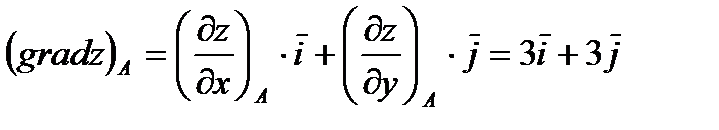
Правило Лопиталя
Задача 1.Вычислить 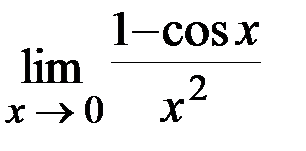 .
.
Решение: 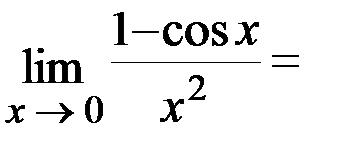
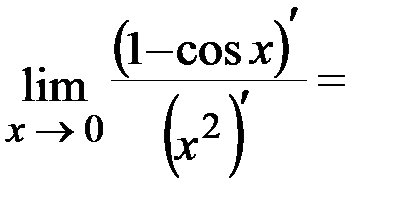
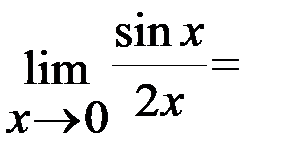
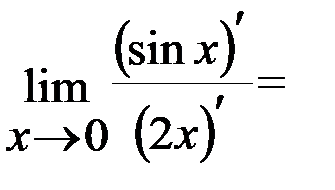
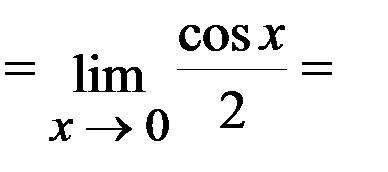
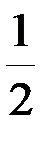 .
.
Задача 2.Вычислить 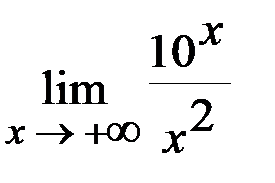 .
.
Решение:
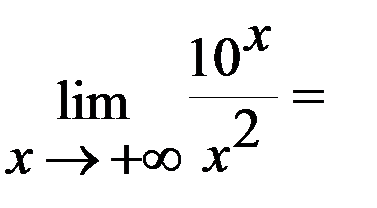
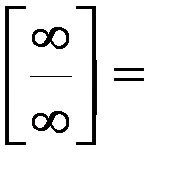
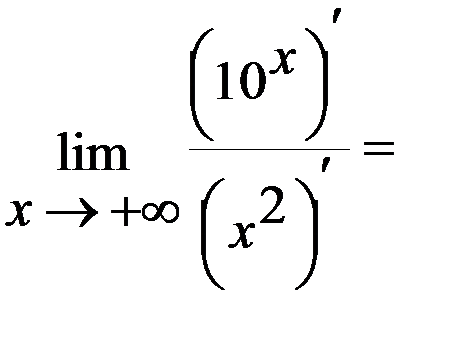
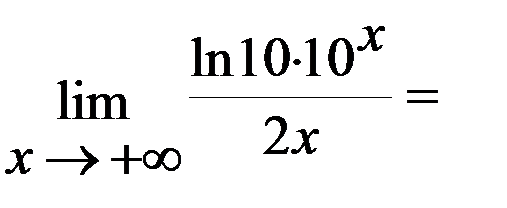

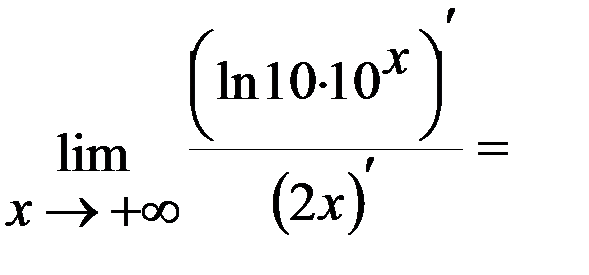
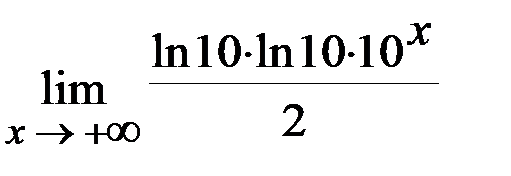
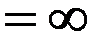 .
.
Задача 3. Вычислить 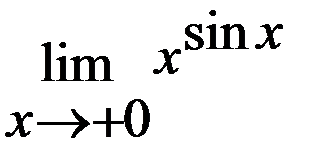 .
.
Решение:
Ясно, что рассматриваемый предел представляет собой неопределенность типа  . Логарифмируем выражение
. Логарифмируем выражение 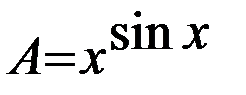 , получаем
, получаем 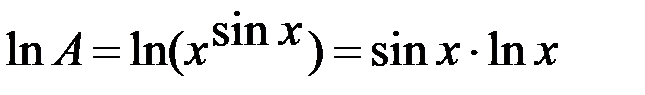 .
.
С учетом последнего равенства находим
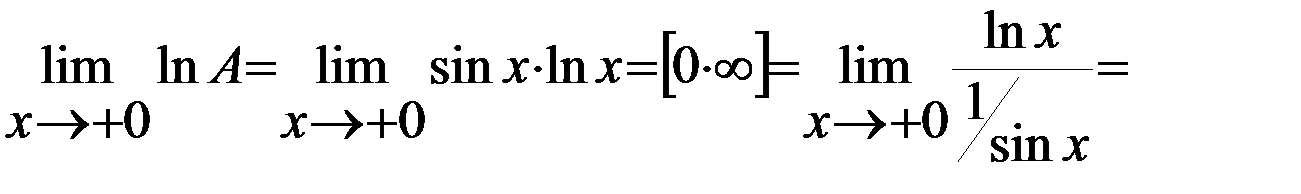
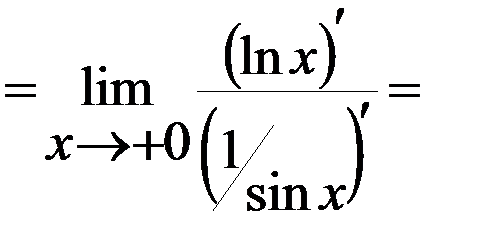
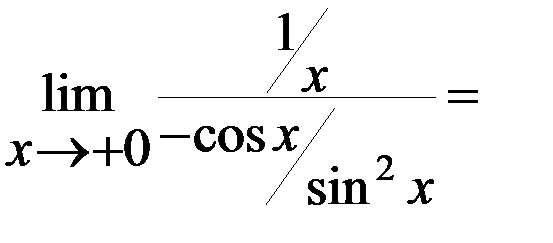
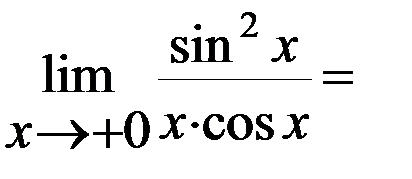
= 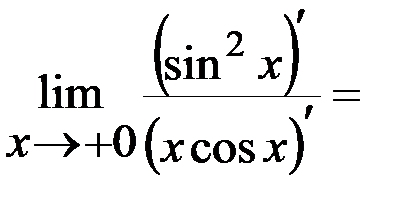
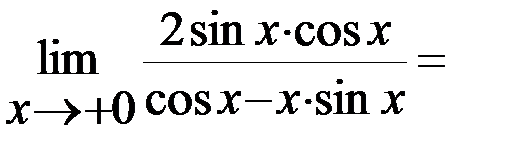 0.
0.
Воспользовавшись непрерывностью функции 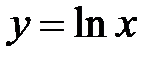 на вcей естественной области определения, получим:
на вcей естественной области определения, получим: 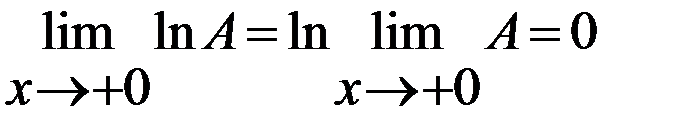 . Отсюда
. Отсюда 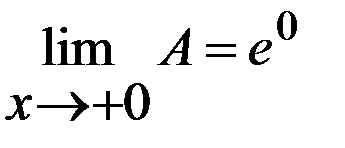 =1.
=1.
Следовательно, 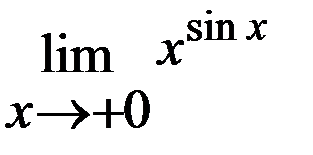 =1.
=1.
Найти значения пределов:
№1
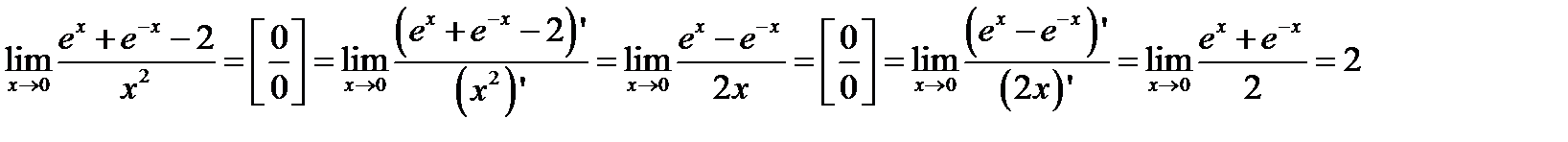
№2 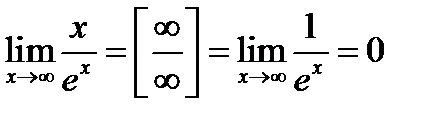
№3. 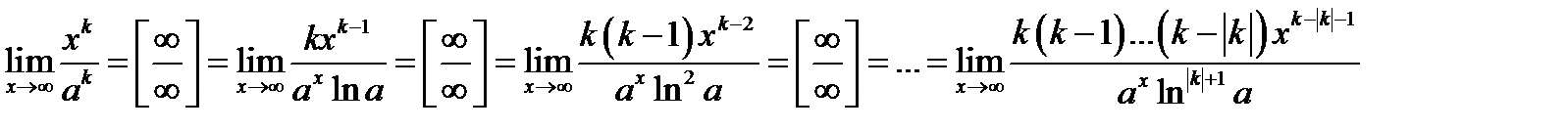
№4. 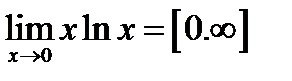 Перепишем данное выражение в виде
Перепишем данное выражение в виде 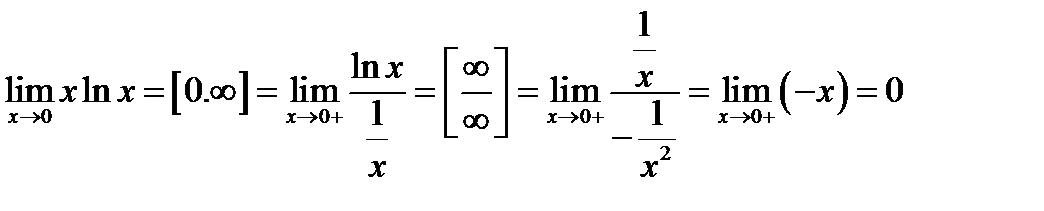 .
.
№5 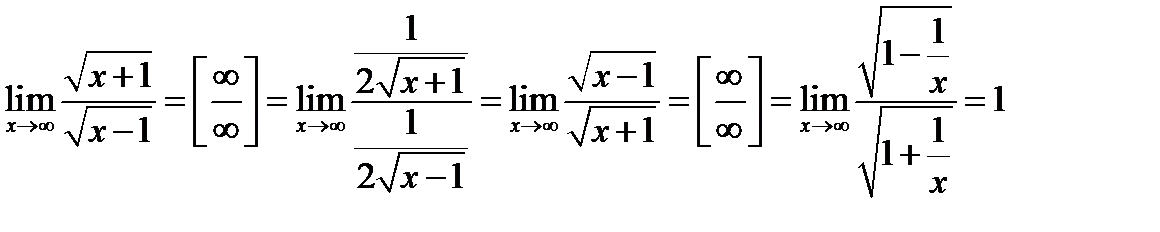 .
.
№6. 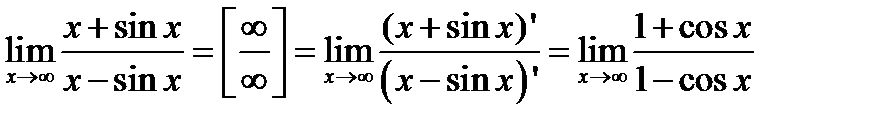 . В этом случае применение правила Лопиталя ошибочно, лучше сделать преобразования
. В этом случае применение правила Лопиталя ошибочно, лучше сделать преобразования 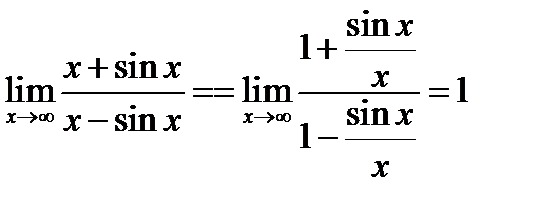 , т.к.
, т.к. 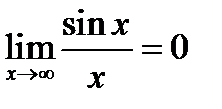
№7. 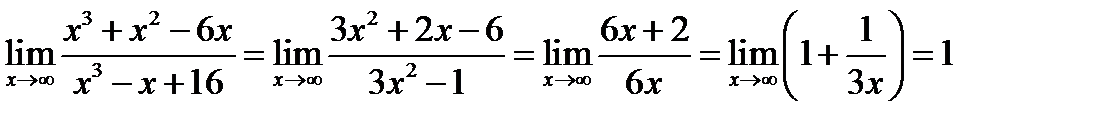 .
.
№8. 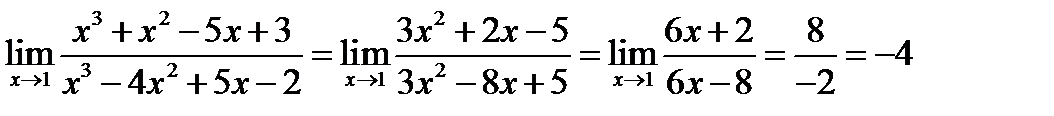 .
.
№9. 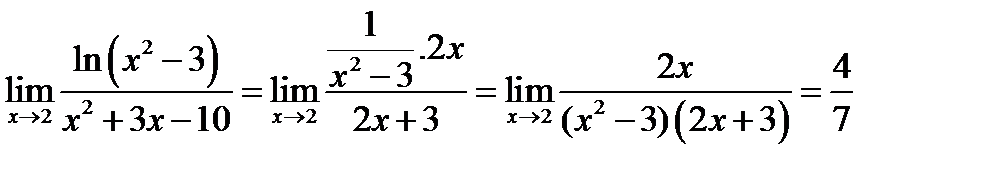 .
.
№10. 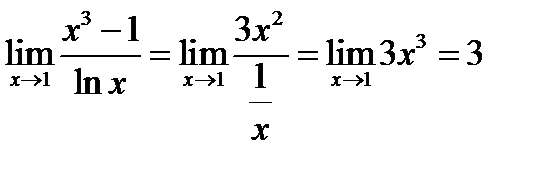 .
.
№11. 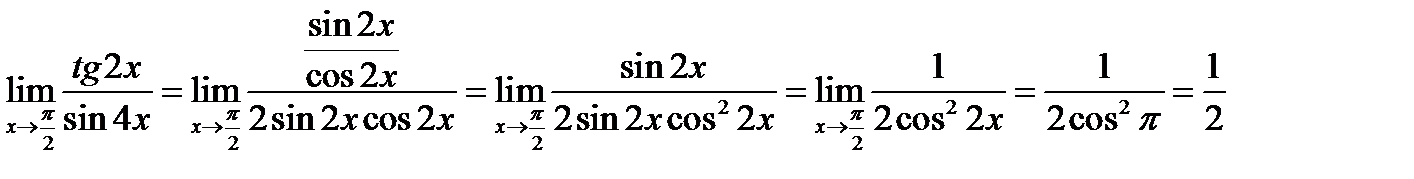
или 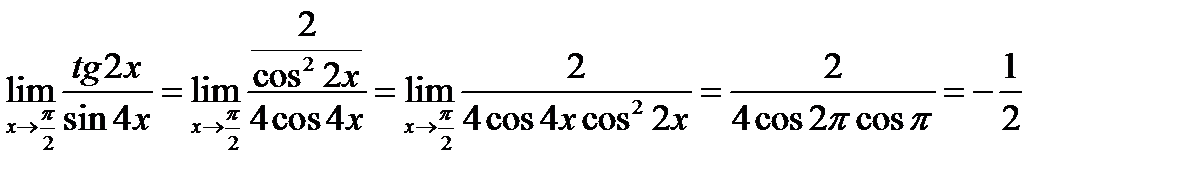 .
.
№12. 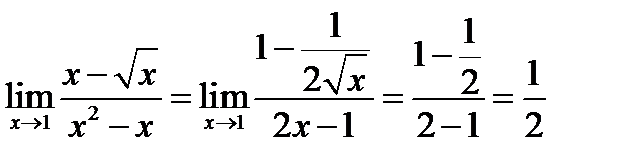 .
.
№13. 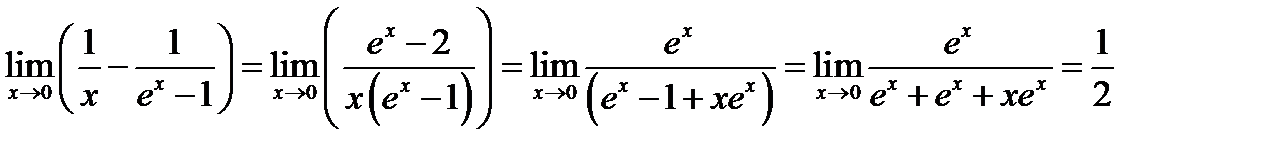 .
.
№14. 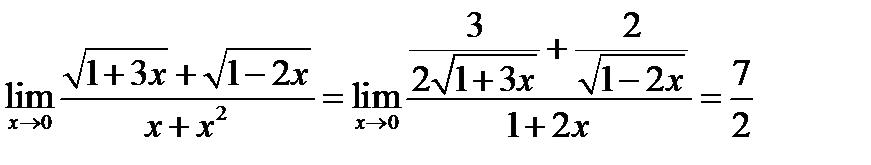 .
.
№15. 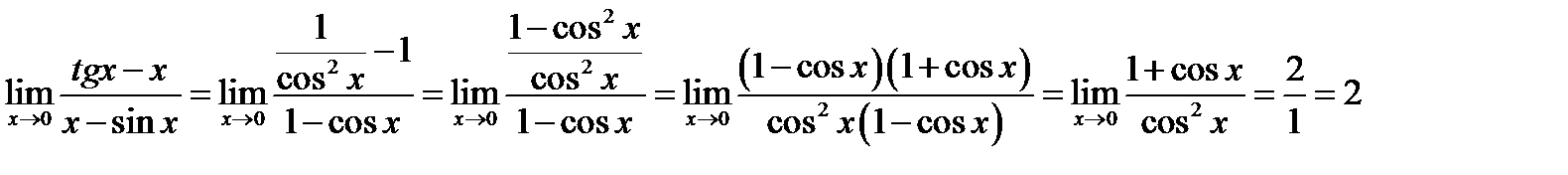 .
.
№ 16. 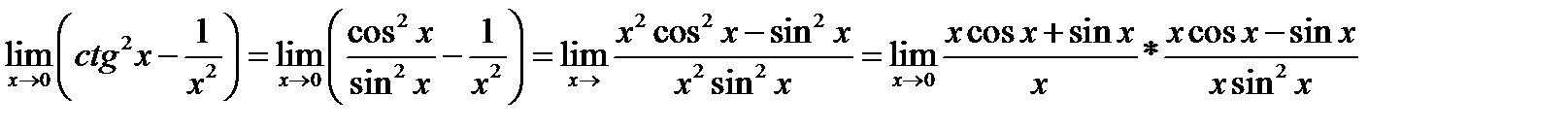
предел первого множителя 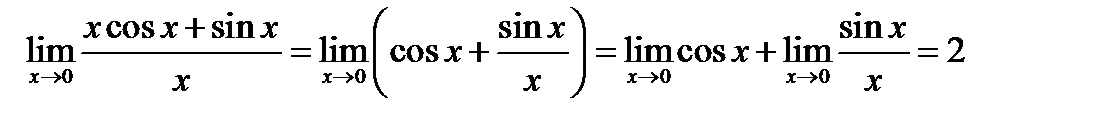
предел второго множителя: 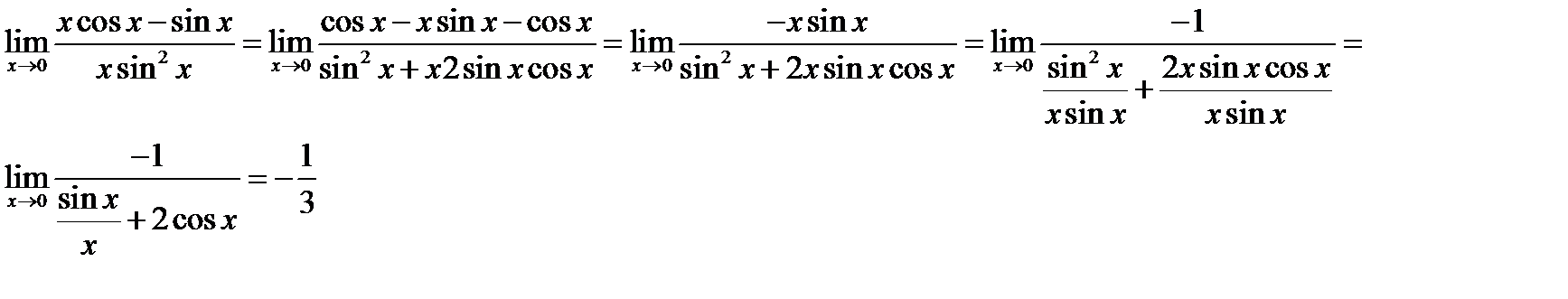 Таким образом, искомый предел равен
Таким образом, искомый предел равен 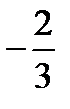 .
.
№17. 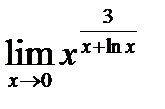 =(логарифмируем заданную функцию, применяем свойство степени, получаем)=
=(логарифмируем заданную функцию, применяем свойство степени, получаем)= 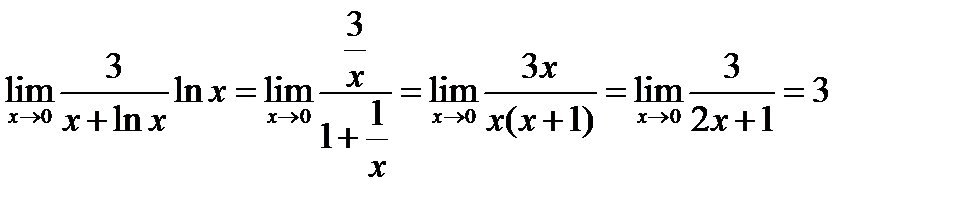 .
.
№18
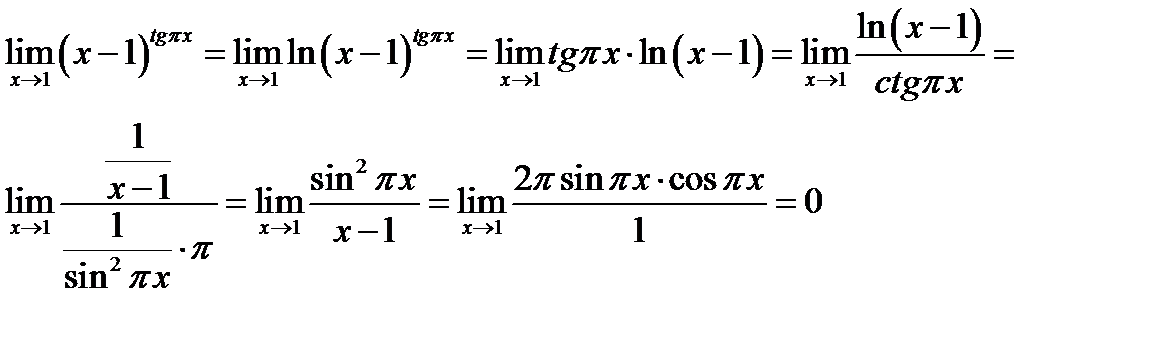
№19. 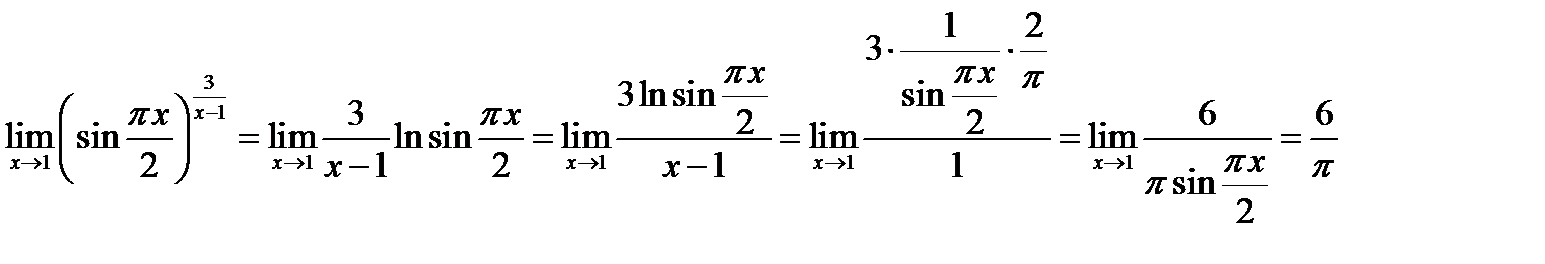
Нахождение промежутков монотонности, экстремумов функции
Пример: Исследовать на максимум и минимум функцию.
а) 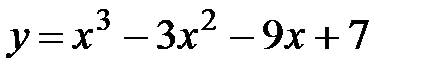 .
.
1. Область определения функции D(y)=R.
2. 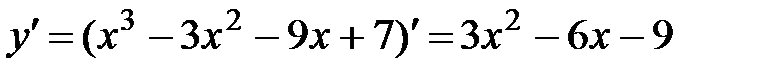 .
.
Критические точки: 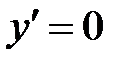 .
. 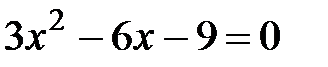 ,
, 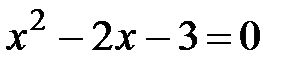 Þ
Þ 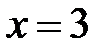 ,
, 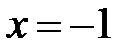 .
.
3. 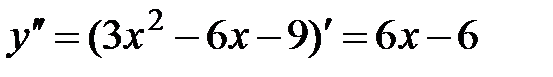 .
.
| x | x=-1 | x=3 |
 | -12 | |
 | max y(-1)=12 | min y(3)=-20 |
б) 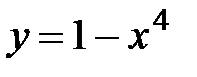 .
.
1. Область определения функции D(y)=R.
2. 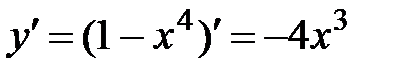 .
.
Критические точки: 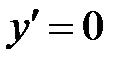 .
. 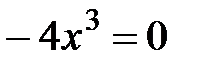 Þ
Þ 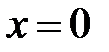 .
.
3. 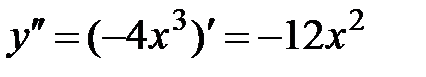 .
.
| x | (-∞;0) | x=0 | (0;+∞) |
 | Наши рекомендации
|
