К решению задач и выполнению
КОНТРОЛЬНЫХ РАБОТ
1. Часть 2 «Методических указаний к выполнению контрольных работ» предназначена для решения 2-х последних контрольных работ по общей физике студентами-заочниками Института механизации и технического сервиса (ИМ и ТС) с 6-летним сроком обучения и второй контрольной работы студентами ИМ и ТС с сокращённым сроком обучения.
2. Номера задач, которые студент с 6-летним сроком обучения должен включить в свои контрольные работы, определяются по таблицам вариантов на страницах 17 и 31. Номер варианта совпадает с последней цифрой шифра студента.
3. Для выполнения второй контрольной работы студент ИМ и ТС с сокращённым сроком обучения должен решить 4 задачи (1-ую, 3-ю, 5-ю и 7-ю) своего варианта (номер варианта совпадает с последней цифрой шифра студента) из таблицы на странице 17 и соответственно 4 задачи своего варианта из таблицы на странице 31 (всего 8 задач).
4. Контрольные работы нужно выполнять в школьной тетради, на обложке которой привести сведения, например, по следующему образцу:
Контрольная работа №3 по физике.
Студент ИМ и ТС 2-го курса
Киселев А. В., Шифр 07-25
Адрес: г. Альметьевск,
ул. Сергеева, 2, кв. 5.
5. Условия задач в контрольной работе надо переписать полностью без сокращений. Для замечаний преподавателя на страницах тетради оставлять поля.
6. В конце контрольной работы указать, каким учебником или учебным пособием студент пользовался при изучении физики (название учебника, автор, год издания). Это делается для того, чтобы рецензент в случае необходимости мог указать, что следует студенту изучить для завершения контрольной работы.
7. Высылать на рецензию следует одновременно не более одной работы. Во избежание одних и тех же ошибок очередную работу следует высылать только после получения рецензии на предыдущую. Если контрольная работа при рецензировании не зачтена, студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными. Повторную работу необходимо представить вместе с не зачтенной.
8. Зачтенные контрольные работы предъявляются экзаменатору. Студент должен быть готов дать пояснения по существу решения задач, входящих в контрольные работы.
9. Решения задач следует сопровождать краткими, но исчерпывающими пояснениями; в тех случаях, когда это возможно, дать чертеж, выполненный с помощью чертежных принадлежностей.
10. Решать задачу надо в общем виде: т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.
11. После получения расчетной формулы для проверки правильности ее следует подставить в правую часть формулы вместо символов величин обозначения единиц этих величин, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.
12. Числовые значения величин при подстановке их в расчетную формулу следует выражать только в единицах СИ. В виде исключения допускается выражать в любых, но одинаковых единицах числовые значения однородных величин, стоящих в числителе и знаменателе дроби и имеющих одинаковые степени.
13. При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с однозначащей цифрой перед запятой на соответствующую степень десяти.
Например, вместо 3520 надо записать 3,52∙103, вместо 0.00129 записать 1,29∙10-3 и т.п.
14. Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений. Как правило, окончательный ответ следует записывать с тремя значащими цифрами.
ЭЛЕКТРИЧЕСТВО, МАГНЕТИЗМ, КОЛЕБАНИЯ И ВОЛНЫ
ОСНОВНЫЕ ФОРМУЛЫ
Закон Кулона где q1 и q2 – величины точечных зарядов; 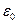 - электрическая постоянная; - электрическая постоянная; 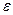 - диэлектрическая проницаемость среды; r – расстояние между зарядами. Напряженность электрического поля Напряженность поля: точечного заряда бесконечно длинной заряженной нити равномерно заряженной бесконечной плоскости между двумя разноименно заряженными бесконечными плоскостями где - диэлектрическая проницаемость среды; r – расстояние между зарядами. Напряженность электрического поля Напряженность поля: точечного заряда бесконечно длинной заряженной нити равномерно заряженной бесконечной плоскости между двумя разноименно заряженными бесконечными плоскостями где 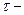 линейная плотность заряда линейная плотность заряда  ; ; 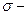 поверхностная плотность заряда поверхностная плотность заряда 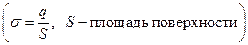 ; r – расстояние до источника поля. Принцип суперпозиции электрических полей Вектор электрической индукции ; r – расстояние до источника поля. Принцип суперпозиции электрических полей Вектор электрической индукции 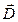 Работа перемещения заряда в электростатическом поле где Работа перемещения заряда в электростатическом поле где 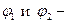 потенциалы начальной и конечной точек. Потенциал поля точечного заряда Связь между потенциалом и напряженностью Электроемкость: уединенного проводника плоского конденсатора Электроемкость батареи конденсаторов, соединенных параллельно последовательно Энергия поля: заряженного проводника заряженного конденсатора Объемная плотность энергии электрического поля Сила тока Плотность тока Закон Ома: для участка цепи: для полной (замкнутой) цепи где потенциалы начальной и конечной точек. Потенциал поля точечного заряда Связь между потенциалом и напряженностью Электроемкость: уединенного проводника плоского конденсатора Электроемкость батареи конденсаторов, соединенных параллельно последовательно Энергия поля: заряженного проводника заряженного конденсатора Объемная плотность энергии электрического поля Сила тока Плотность тока Закон Ома: для участка цепи: для полной (замкнутой) цепи где 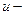 напряжение на концах цепи, R – сопротивление участка цепи, r – внутреннее сопротивление источника тока, напряжение на концах цепи, R – сопротивление участка цепи, r – внутреннее сопротивление источника тока, 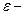 ЭДС источника тока. Сопротивление проводника где ЭДС источника тока. Сопротивление проводника где 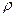 - удельное сопротивление однородногопроводника; - удельное сопротивление однородногопроводника; 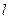 - длина проводника; S - площадь его поперечного сечения. Зависимость сопротивления проводника от температуры где - длина проводника; S - площадь его поперечного сечения. Зависимость сопротивления проводника от температуры где 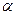 - температурный коэффициент сопротивления; t - температура по шкале Цельсия; R0 - сопротивления проводника при 00С. Сопротивление системы проводников: а) при последовательном соединении б) при параллельном соединении, где Ri - сопротивление i- го проводника. Работа тока Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две - для участка не содержащего ЭДС. Мощность тока Закон Джоуля-Ленца Сила Лоренца где - температурный коэффициент сопротивления; t - температура по шкале Цельсия; R0 - сопротивления проводника при 00С. Сопротивление системы проводников: а) при последовательном соединении б) при параллельном соединении, где Ri - сопротивление i- го проводника. Работа тока Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две - для участка не содержащего ЭДС. Мощность тока Закон Джоуля-Ленца Сила Лоренца где 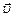 - скорость заряда ; - скорость заряда ; 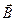 - индукция магнитного поля. Сила Ампера где - индукция магнитного поля. Сила Ампера где 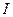 - сила тока в проводнике; - сила тока в проводнике; 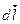 - элемент длины проводника. Магнитный момент контура с током где - элемент длины проводника. Магнитный момент контура с током где 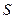 - площадь контура. Магнитная индукция: в центре кругового тока поля бесконечно длинного прямого тока поля, созданного отрезком проводника с током, поля бесконечно длинного соленоида где - площадь контура. Магнитная индукция: в центре кругового тока поля бесконечно длинного прямого тока поля, созданного отрезком проводника с током, поля бесконечно длинного соленоида где 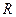 - радиус кругового тока; - радиус кругового тока; 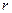 кратчайшее расстояние до оси проводника; кратчайшее расстояние до оси проводника; 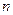 - число витков на единицу длины соленоида; - число витков на единицу длины соленоида; 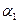 и и 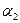 - углы между направлением тока в проводнике и радиус – векторами, проведенными от концов проводника в точку, где определяется индукция магнитного поля. Сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников с током на длину проводника - углы между направлением тока в проводнике и радиус – векторами, проведенными от концов проводника в точку, где определяется индукция магнитного поля. Сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников с током на длину проводника 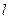 где где 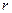 - расстояние между проводниками тока - расстояние между проводниками тока 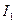 и и 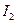 . Работа по перемещению контура с током в магнитном поле где Ф – магнитный поток через поверхность контура. Магнитный поток однородного магнитного через площадку S где . Работа по перемещению контура с током в магнитном поле где Ф – магнитный поток через поверхность контура. Магнитный поток однородного магнитного через площадку S где 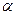 - угол между вектором - угол между вектором 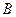 и нормалью к площадке. Закон электромагнитной индукции где и нормалью к площадке. Закон электромагнитной индукции где 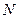 - число витков контура. Потокосцепление контура с током где - число витков контура. Потокосцепление контура с током где 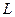 - индуктивность контура. Электродвижущая сила самоиндукции Индуктивность соленоида где - индуктивность контура. Электродвижущая сила самоиндукции Индуктивность соленоида где 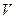 - объем соленоида; - объем соленоида; 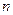 - число витков на единицу длины соленоида. Энергия магнитного поля Объемная плотность энергии магнитного поля Период колебаний в электрическом колебательном контуре где L - индуктивность контура; С – емкость конденсатора. Длина волны где Т- период волны. Скорость распространения электромагнитной волны где - число витков на единицу длины соленоида. Энергия магнитного поля Объемная плотность энергии магнитного поля Период колебаний в электрическом колебательном контуре где L - индуктивность контура; С – емкость конденсатора. Длина волны где Т- период волны. Скорость распространения электромагнитной волны где 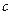 -скорость света в вакууме; -скорость света в вакууме; 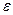 - диэлектрическая проницаемость среды; - диэлектрическая проницаемость среды; 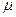 - магнитная проницаемость среды. Сопротивление в колебательном контуре: активное индуктивное емкостное полное где - магнитная проницаемость среды. Сопротивление в колебательном контуре: активное индуктивное емкостное полное где 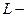 индуктивность катушки; индуктивность катушки; 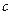 - емкость конденсатора; - емкость конденсатора; 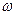 - циклическая частота переменного тока. Сдвиг фаз между напряжением и током в цепи переменного тока Амплитуда силы тока в колебательном контуре при подключении к контуру гармонической ЭДС - циклическая частота переменного тока. Сдвиг фаз между напряжением и током в цепи переменного тока Амплитуда силы тока в колебательном контуре при подключении к контуру гармонической ЭДС 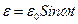 . . | 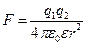 , , 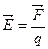 . . 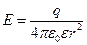 ; ; 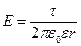 ; ; 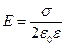 ; ; 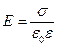 , , 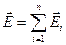 . . 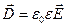 . . 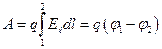 , , 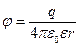 . . 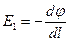 . . 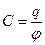 ; ; 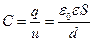 . . 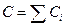 ; ; 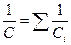 . . 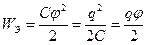 ; ; 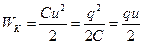 . . 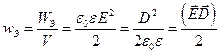 . . 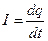 . . 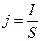 . . 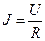 ; ; 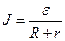 , R= , R= 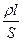 , R=R0(1+ , R=R0(1+ 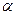 t), t), 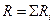
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Заряды q1= 3нКл и q2= -5 нКл находятся на расстоянии r = 6см друг от друга. Определить напряженность Е и потенциал φ в точке, находящейся на расстоянии a = 3 см от первого заряда и d = 4 см от второго заряда. Какой силой потребуется удержать в этой точке заряд q 3 = 1нКл?
Решение. Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность 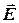 электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей
электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей 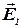 и
и 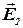 полей, создаваемых каждым зарядом в отдельности:
полей, создаваемых каждым зарядом в отдельности: 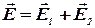 .
.
Напряженность электрического поля, создаваемого в воздухе (ε = 1) зарядом q1, равна
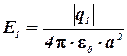
зарядом q2 -
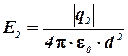
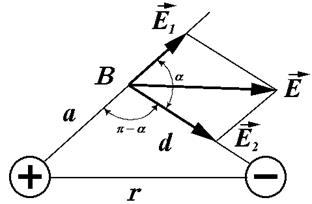 Рис. 1.1 Рис. 1.1 |
Вектор 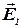 направлен по силовой линии от заряда, так как заряд q1 положителен; вектор
направлен по силовой линии от заряда, так как заряд q1 положителен; вектор 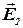 направлен также по силовой линии, но к заряду q2 , так как заряд q2 отрицателен.
направлен также по силовой линии, но к заряду q2 , так как заряд q2 отрицателен.
Абсолютное значение вектора Е найдтся по теореме косинусов:
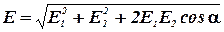 ,
,
где α - угол между векторами 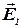 и
и 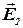 , который может быть найден из треугольника со сторонами r, a, d:
, который может быть найден из треугольника со сторонами r, a, d:
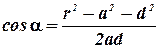
В данном случае во избежание громоздких записей удобно значение cos α вычислить отдельно:
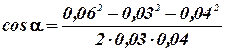 ≈ 046
≈ 046
Подставляя выражения 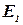 и
и 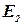 в
в 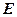 и вынося общий множитель
и вынося общий множитель 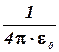 за знак корня, можно получить:
за знак корня, можно получить:
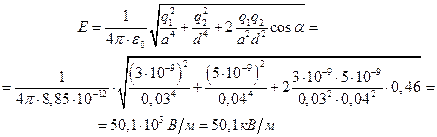
Силу F, которая потребуется, чтобы удержать заряд в точке В, находят по формуле
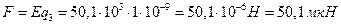
Потенциал j результирующего поля, создаваемого двумя зарядами q1 и q2 , равен алгебраической сумме потенциалов, т.е.
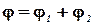
Потенциал электрического поля, создаваемого в вакууме точечным зарядом q на расстоянии r от него, выражается формулой
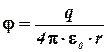
В данном случае 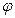 выразится как:
выразится как:
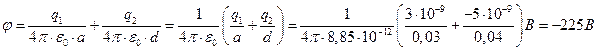
Ответ: 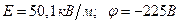
Пример 2. Пластины плоского конденсатора, заряженные зарядом q= 15нКл, притягиваются в воздухе с силой F= 600мкН. Определить площадь пластин конденсатора.
Решение. Заряд q одной пластины находится в поле напряженностью Е1 , созданном зарядом другой пластины конденсатора. Следовательно, на первый заряд действует сила
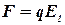
Так как
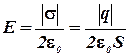 ,
,
где σ - поверхностная плотность заряда пластины, то
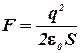 .
.
Тогда
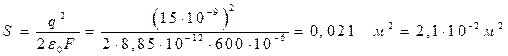
Ответ: 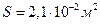
Пример 3. Заряд величиной 1 нКл переносится из бесконечности в точку, находящуюся на расстоянии 0,1 м от поверхности металлической сферы радиусом 0,1 м, заряженной с поверхностной плотностью 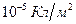 . Определить работу перемещения заряда
. Определить работу перемещения заряда
Дано: 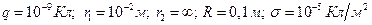 .
.
Найти: A.
Решение. Потенциал поля 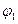 , создаваемого заряженной сферой на расстоянии
, создаваемого заряженной сферой на расстоянии 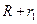 от ее центра, определяется по формуле:
от ее центра, определяется по формуле:
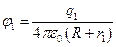 ,
,
где 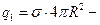 заряд сферы;
заряд сферы; 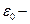 электрическая постоянная.
электрическая постоянная.
Потенциал поля на расстоянии 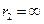 равен нулю:
равен нулю: 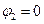 . Работа А по перемещению заряда q из бесконечности в точку поля равна:
. Работа А по перемещению заряда q из бесконечности в точку поля равна:
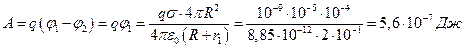
Ответ: 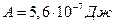
Пример 4. Энергия плоского воздушного конденсатора 40 нДж, разность потенциалов на обкладках 600 В, площадь пластин 1 см2. Определить расстояние между обкладками, напряженность и объемную плотность энергии поля конденсатора.
Дано: 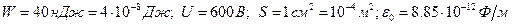 .
.
Найти: 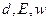
Решение. Энергия конденсатора 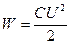 ; емкость конденсатора
; емкость конденсатора 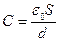 , следовательно,
, следовательно, 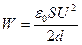 . Отсюда
. Отсюда
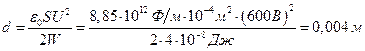 .
.
Напряженность поля конденсатора
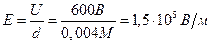
Объемная плотность энергии поля:
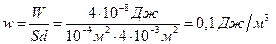
Ответ: 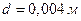 ;
; 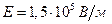 ;
; 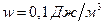 .
.
Пример 5. Электрон, обладающий кинетической энергией Т1= 10эВ, влетел в однородное электрическое поле с напряженностью Е= 10В/м в направлении поля и прошел в нем расстояние r= 50 см. Определить скорость электрона в конце указанного пути.
Решение. В соответствии с определением вектора напряженности электрического поля 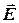 , на электрон, влетевший в направлении вектора напряженности поля, действует сила
, на электрон, влетевший в направлении вектора напряженности поля, действует сила 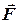 , направленная противоположно движению. Следовательно, электрон тормозится под действием этой силы. На пути движения электрона электрическое поле совершает работу А.
, направленная противоположно движению. Следовательно, электрон тормозится под действием этой силы. На пути движения электрона электрическое поле совершает работу А.
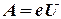 ,
,
где е - заряд электрона; е = 1,6٠10-19Кл.U - разность потенциалов на пути движения.
Работа сил электрического поля, затраченная на изменение кинетической энергии электрона
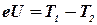 ,
,
где Т1, Т2 - кинетические энергии электрона до и после прохождения замедляющего поля.
Кинетическая энергия электрона в конце пути
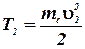 ,
,
где me - масса электрона; υ2 - скорость электрона в конце пути.
Учитывая однородность электрического поля можно написать, что:
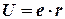
Воспользовавшись указанными формулами, можно получить:
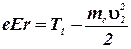
Тогда скорость электрона в конце пути
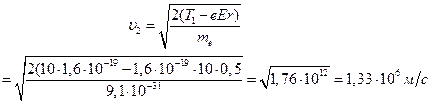
Ответ: 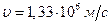
Пример 6. На концах медного провода длиной l = 5м поддерживается напряжение U= 1В. Определить плотность тока j в проводе.
Решение. По закону Ома в дифференциальной форме
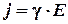
Удельная проводимость γ определяется как
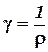 ,
,
где ρ - удельное сопротивление меди 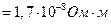
Напряженность электрического поля внутри проводника согласно формуле, связывающей разность потенциалов (напряжение) и напряженность в однородном электрическом поле выражается формулой
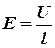
Используя вышеуказанные формулы:
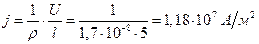
Ответ: 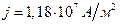
Пример 7. Определить электрический заряд, прошедший через поперечное сечение провода сопротивлением R= 3Ом при равномерном нарастании напряжения на концах провода от U1= 2В до U2= 4В в течение Δt= 20с.
Решение. В соответствии с законом Ома переменное напряжение вызывает в проводнике переменный ток. По определению силы тока
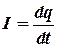 ,
,
отсюда
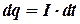 ,
,
где dq - количество электрического заряда, прошедшего через поперечное сечение проводника за бесконечно малый промежуток времени dt, I - мгновенное значение силы переменного тока.
По закону Ома
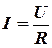 ,
,
где U - мгновенное значение напряжения.
При равномерном нарастании напряжения его мгновенное значение в момент времени t равно
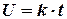 ,
,
где k - скорость нарастания напряжения, равная приращению напряжения за единицу времени. При равномерном нарастании
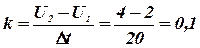 В/ с
В/ с
Используя вышеуказанные формулы, можно вычислить 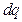
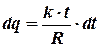
Заряд q, прошедший через поперечное сечение провода за конечный промежуток времени от t1 от t1= 0с, до t2= 20с определяется как:
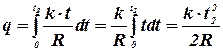
Подставляем значения k, t2 и R:
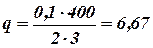 Кл
Кл
Ответ: q=6,67 Кл
Пример 8. Сила тока в проводнике сопротивлением R= 20Ом нарастает в течение времени Δt= 2с по линейному закону от I0= 0 до I= 6А. Определить теплоту Q1, выделившуюся в этом проводнике за первую и Q2 - за вторую секунды, а также найти отношение 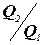 .
.
Решение. По закону Джоуля-Ленца
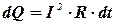
Здесь сила тока является некоторой функцией времени:
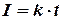 ,
,
где k - коэффициент пропорциональности, численно равный приращению силы тока в единицу времени. При линейном законе
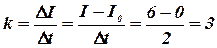 A/ с
A/ с
Тогда 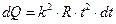 и
и 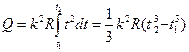
При определении теплоты, выделившейся за первую секунду, пределы интегрирования t1= 0, t2= 1 c и, следовательно,
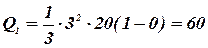 Дж
Дж
При определении теплоты Q2 пределы интегрирования t1= 1, t2= 2 c и
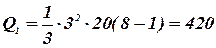 Дж.
Дж.
Следовательно,
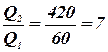
т.е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую.
Пример 9. По проводу, согнутому в виде квадрата со стороной a = 10см течет ток силой I = 100A. Найти магнитную индукцию 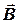 в точке пересечения диагоналей квадрата.
в точке пересечения диагоналей квадрата.
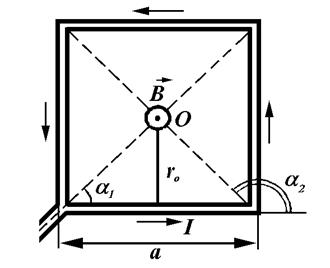 |
Решение. Квадратный виток расположен в плоскости чертежа.
Согласно принципу суперпозиции магнитных полей магнитная индукция поля 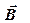 квадратного витка будет равна геометрической сумме магнитных индукций полей, создаваемых каждой стороной квадрата в отдельности:
квадратного витка будет равна геометрической сумме магнитных индукций полей, создаваемых каждой стороной квадрата в отдельности:
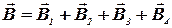
В точке О пересечения диагоналей квадрата все векторы индукции для указанного на рис. тока будут направлены перпендикулярно плоскости витка «к нам». Кроме того, из соображений симметрии следует, что абсолютные значения этих векторов одинаковы: 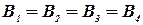 . Это позволяет векторное равенство заменить скалярным равенством
. Это позволяет векторное равенство заменить скалярным равенством
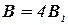
Магнитная индукция В1 поля, создаваемого отрезком прямолинейного провода с током, выражается формулой
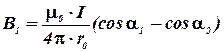
Учитывая, что 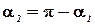 и
и 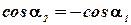 , формулу можно переписать в виде
, формулу можно переписать в виде
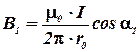 и учитывая, что В=4В1
и учитывая, что В=4В1
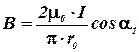
Здесь 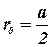 и
и 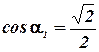 (так как
(так как 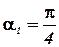 ), и тогда В.
), и тогда В.
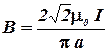
Подставив в эту формулу числовые значения физических величин, для В получится значение:
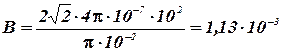 Tл.
Tл.
Пример 10. Электрон, пройдя ускоряющую разность потенциалов U = 400В, попал в однородное магнитное поле напряженностью H = 103А/м. Определить радиус R кривизны траектории и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.
Решение. Радиус кривизны траектории электрона можно определить, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца 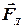 (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение:
(действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение:
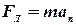
или
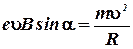 ,
,
где е - заряд электрона, υ - скорость электрона, В- магнитная индукция, m - масса электрона,
R - радиус кривизны траектории, α - угол между направлением вектора скорости 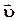 и вектором
и вектором 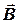 (в данном случае
(в данном случае 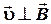 и α = 90°, sinα = 1)
и α = 90°, sinα = 1)
Тогда для R находится формула:
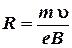
Входящий в это равенство импульс mυ может быть выражен через кинетическую энергию Т электрона:
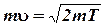
Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством
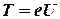
Подставив это выражение Т в выражение для 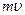 получится выражение:
получится выражение:
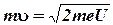
Магнитная индукция В может быть выражена через напряженность Н магнитного поля в вакууме
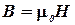 ,
,
где μ0 - магнитная постоянная.
Используя полученные выражения можно определить R в виде:
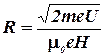
Здесь: m=9,11٠10‑31 кг, e = 1,60٠10-19 Кл, U = 400 В, μ0 = 4π٠10-7 Гн/м, Н = 103 А/м.
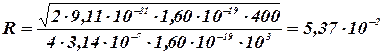 м = 5,37см
м = 5,37см
Для определения частоты обращения n можно воспользоваться формулой, связывающей частоту со скоростью и радиусом:
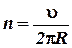
С учетом 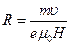 получится:
получится:
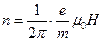
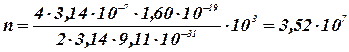 c-1
c-1
Ответ: 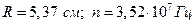
Пример 11. В однородном магнитном поле (В = 0,1 Тл) равномерно с частотой n = 10об/с вращается рамка, содержащая N = 1000 витков, плотно прилегающих друг к другу. Площадь рамки S = 150см2. Определить мгновенное значение Э.Д.С. индукции 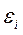 , соответствующее углу поворота рамки 30°.
, соответствующее углу поворота рамки 30°.
Решение. Мгновенное значение Э.Д.С. индукции 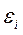 определяется основным уравнением электромагнитной индукции
определяется основным уравнением электромагнитной индукции
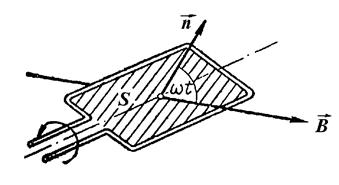 |
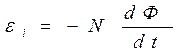
При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, изменяется по закону
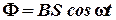 ,
,
где В- магнитная индукция,
S - площадь рамки,
ω - круговая (циклическая) частота.
Продифференцировав по времени Ф, можно найти мгновенное значение Э.Д.С. индукции в виде:
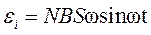
Учитывая, что частота ω связана с частотой вращения n соотношением
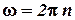 ,
,
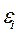 получится как:
получится как:
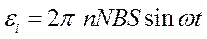
По условию задачи: n= 10c-1; N = 103; B = 0,1 Tл; S = 1,5٠10-2 м2; ωt = 30° = 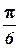 и, подставив их в
и, подставив их в 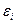 можно найти:
можно найти:
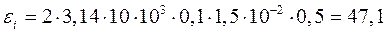 В
В
Ответ: 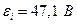
Пример 12. Соленоид без сердечника имеет плотную однослойную намотку провода диаметром 0,2 мм и по нему течет ток 0,1 А. Длина соленоида 20 см, диаметр 5 см. Найти энергию и объемную плотность энергии магнитного поля соленоида.
Дано: 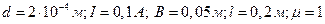 .
.
Найти: 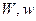 .
.
Решение. Энергия магнитного поля соленоида 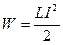 , где
, где 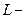 индуктивность соленоида,
индуктивность соленоида, 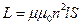 ;
; 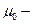 магнитная постоянная; n – число витков на 1 м длины соленоида, при плотной намотке
магнитная постоянная; n – число витков на 1 м длины соленоида, при плотной намотке 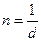 ;
; 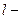 длина соленоида;
длина соленоида; 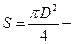 площадь сечения соленоида. Тогда:
площадь сечения соленоида. Тогда:
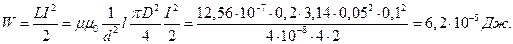 .
.
Объемная плотность энергии определяется по формуле:
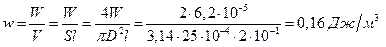
Ответ: 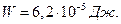 ;
; 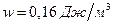 .
.
Пример 13. Конденсатору емкостью 40 мкФ сообщен заряд 0,3 мКл, после чего его замыкают на катушку с индуктивностью 0,1 Гн. Пренебрегая сопротивлением контура, найти законы изменения напряжения на конденсаторе и силы тока в цепи.
Дано: 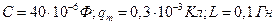 .
.
Найти: 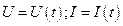 .
.
Решение. В отсутствие омического сопротивления свободные колебания в контуре описываются уравнением
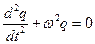 (1)
(1)
где 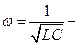 циклическая частота колебаний.
циклическая частота колебаний.
Решение уравнения (1) имеет вид
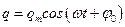 , (2)
, (2)
где 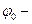 начальная фаза колебаний. Поскольку в начальный момент времени
начальная фаза колебаний. Поскольку в начальный момент времени 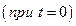 заряд конденсатора
заряд конденсатора 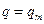 , то
, то 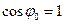 и, следовательно,
и, следовательно, 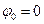 .
.
Напряжение на конденсаторе
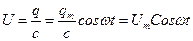 (3)
(3)
а сила тока в цепи
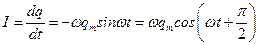 (4)
(4)
Числовые значения, получатся как:
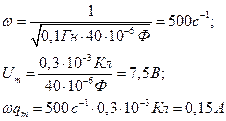
Таким образом, 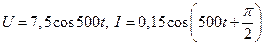
Ответ: 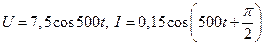 .
.
Контрольная работа 3
Таблица варианта
| Вариант | Номер контрольных работ | |||||||

 .
.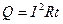 .
.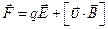 ,
,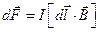 ,
,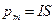 ,
,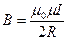 ;
;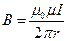 ;
;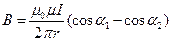 ;
;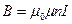 ,
,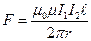 ,
,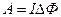 ,
,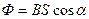 ,
,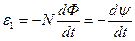 ,
,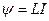 ,
,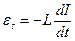 .
.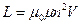 ,
,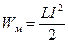 .
.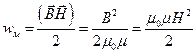 .
.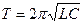 ,
,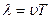 ,
,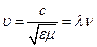 ,
,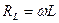
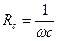
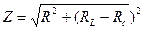 ,
,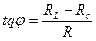 .
.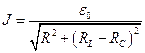 .
.