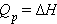Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела

Существует несколько теорий теплоёмкости твердого тела:

• Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).
• Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.
• Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.

Теплоёмкость системы невзаимодействующих частиц (например, идеального газа) определяется числом степеней свободы частиц.

4. Понятия энтальпия

Энтальпия

Энтальпия системы (от греч. enthalpo нагреваю) – это однозначная функция H состояния термодинамической системы при независимых параметрах энтропии S и давлении P, которая связана с внутренней энергией U соотношением

H = U + PV

где V – объем системы.

В химии чаще всего рассматривают изобарические процессы (P = const), и тепловой эффект в этом случае называют изменением энтальпии системы или энтальпией процесса:

ΔH = ΔU + PΔV

(4.1)

Энтальпия имеет размерность энергии (кДж). Ее величина пропорциональна количеству вещества; энтальпия единицы количества вещества (моль) измеряется в кДж∙моль^–1.

В термодинамической системе выделяющуюся теплоту химического процесса условились считать отрицательной (экзотермический процесс, ΔH < 0), а поглощение системой теплоты соответствует эндотермическому процессу, ΔH > 0.

Уравнения химических реакций с указанием энтальпии процесса называют термохимическими. Численные значения энтальпии ΔH указывают через запятую в кДж и относят ко всей реакции с учетом стехиометрических коэффициентов всех реагирующих веществ. Поскольку реагирующие вещества могут находиться в разных агрегатных состояниях, то оно указывается нижним правым индексом в скобках: (т) – твердое, (к) – кристаллическое, (ж) – жидкое, (г) – газообразное, (р) – растворенное. Например, при взаимодействии газообразных H₂ и Cl₂ образуются два моля газообразного HCl. Термохимическое уравнение записывается так:

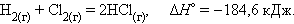При взаимодействии газообразных H₂ и O₂ образующаяся H₂O может находиться в трех агрегатных состояниях, что скажется на изменении энтальпии:

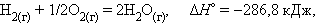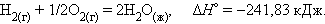Приведенные энтальпии образования веществ и энтальпии реакций отнесены к стандартным условиям (P = 101,325 кПа) и взяты для температуры T = 298 K. Стандартное состояние термодинамической функции, например, энтальпии, обозначается нижним и верхним индексами: 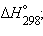нижний индекс обычно опускают: Δ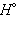

Понятие эндропия

Энтропи́я (от др.-греч. ἐντροπία «поворот», «превращение») — широко используемый в естественных и точных науках термин. Впервые введён в рамках термодинамики как функция состояния термодинамической системы, определяющая меру необратимого рассеивания энергии. В статистической физике энтропия характеризует вероятность осуществления какого-либо макроскопического состояния. Кроме физики, термин широко употребляется в математике: теории информации и математической статистике.

Энтропия может интерпретироваться как мера неопределённости (неупорядоченности) некоторой системы, например, какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации^[1][2]. Таким образом, другой интерпретацией энтропии является информационная ёмкость системы. С данной интерпретацией связан тот факт, что создатель понятия энтропии в теории информации (Клод Шеннон) сначала хотел назвать эту величину информацией.

Понятие информационной энтропии применяется как в теории информации и математической статистике, так и в статистической физике (энтропия Гиббса и её упрощённый вариант — энтропия Больцмана)^[3][4]. Математический смысл информационной энтропии — это логарифм числа доступных состояний системы (основание логарифма может быть различным, оно определяет единицу измерения энтропии)^[5]. Такая функция от числа состояний обеспечивает свойство аддитивности энтропии для независимых систем. Причём, если состояния различаются по степени доступности (то есть не равновероятны), под числом состояний системы нужно понимать их эффективное количество, которое определяется следующим образом. Пусть состояния системы равновероятны и имеют вероятность {\displaystyle p}, тогда число состояний {\displaystyle N=1/p}, а {\displaystyle \log N=\log(1/p).}

В случае разных вероятностей состояний {\displaystyle p_{i}} рассмотрим средневзвешенную величину {\displaystyle \log {\overline {N}}=\sum _{i=1}^{N}p_{i}\log(1/p_{i}),} где {\displaystyle {\overline {N}}} — эффективное количество состояний. Из данной интерпретации непосредственно вытекает выражение для информационной энтропии Шеннона

{\displaystyle H=\log {\overline {N}}=-\sum _{i=1}^{N}p_{i}\log p_{i}.}

Подобная интерпретация справедлива и для энтропии Реньи, которая является одним из обобщений понятия информационная энтропия, но в этом случае иначе определяется эффективное количество состояний системы (можно показать, что энтропии Реньи соответствует эффективное количество состояний, определяемое как среднее степенное взвешенное с параметром {\displaystyle q\leq 1} от величин {\displaystyle 1/p_{i}})^[6].

В широком смысле, в каком слово часто употребляется в быту, энтропия означает меру неупорядоченности или хаотичности системы: чем меньше элементы системы подчинены какому-либо порядку, тем выше энтропия.

6. первый закон термодинамики

Первый закон термодинамики

На рис. 3.9.1 условно изображены энергетические потоки между выделенной термодинамической системой и окружающими телами. Величина Q > 0, если тепловой поток направлен в сторону термодинамической системы. Величина A > 0, если система совершает положительную работу над окружающими телами.

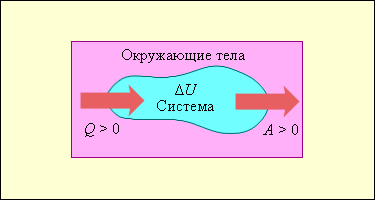Рисунок 3.9.1. Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы

Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, т. е. изменяются ее макроскопические параметры (температура, давление, объем). Так как внутренняя энергия U однозначно определяется макроскопическими параметрами, характеризующими состояние системы, то отсюда следует, что процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы.

Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:

Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.

ΔU = Q – A.

Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:

Q = ΔU + A.