Глава 6. интегралы функций одной переменной

ГЛАВА 6. ИНТЕГРАЛЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Неопределённый интеграл. Определение и свойства

В дальнейшем под промежутком Х будем понимать одноиз следующих множеств (а,b), .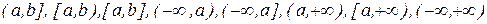

Определение 1. Функция F(x) называетсяпервообразнойдля f(x) на промежутке Х если выполняются следующие условия:

а) функция f(x) определена на промежутке Х;

б) функция F(x)непрерывна и дифференцируема во всех внутренних точках Х;

в) .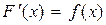

Примеры. 1) 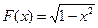является первообразной для функции 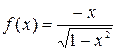на промежутке Х=(-1,1).

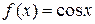2) является первообразной для функции на промежутке .

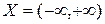3) 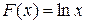является первообразной для функции 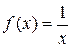на промежутке .

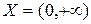Из определения 1 очевидно, что если F(x) является первообразной для f(x), то F(x) + C также является первообразной для этой функции. Как отличаются между собой две первообразные?

Теорема 1. Есл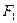и (x) и 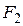(x) две первообразные для f(x)на промежутке Х, то всюду на этом интервале 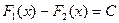, где С - произвольная постоянная.

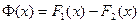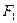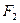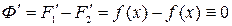
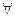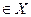□Положим . Т.к. и дифференцируемы на Х, то Ф(х) дифференцируема на Х следовательно x и 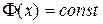, откуда . ■

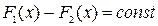Следствие.Если F(x) одна из первообразных для f(x) на Х, то любая другая первообразная Ф(х) для f(x) на Х имеет вид 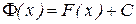, где С – произвольная постоянная.

Определение 2. Множество всех первообразных функций f(x) на промежутке X называется неопределённым интегралом от функции f(x) на Х и обозначается 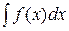. Функция f(x) называетсяподынтегральной функцией. Обозначение неопределенного интеграла

.

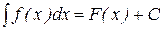Под знаком интеграла 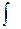пишут для удобства не только саму функцию но и дифференциал dx для того, чтобы указать по какой переменной ищется первообразная.

Примеры.

1) 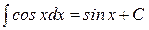на .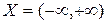

2) 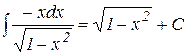, -1<x<1

Свойства интегралов

1. 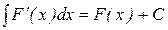или 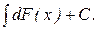Справедливость следует из определения.

2. 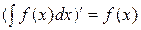или .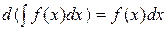

□ . ■

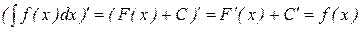3. Постоянный множитель можно выносить за знак интеграла, т.е. если a= const 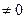, то

.

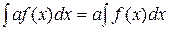□ Пусть F(x) – первообразная для f(x), т.е. 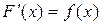. Тогда аF(x)первообразная для af(x), т.к. 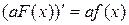. Тогда по определению

. ■

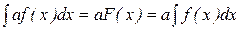4. Неопределённый интеграл от алгебраической суммы двух функций равен сумме неопределённых интегралов от этих функций, т.е.

.

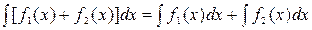□ Пусть 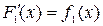и 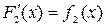, тогда функция 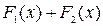- первообразная для 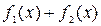, т.к. 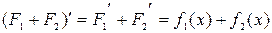. По определению имеем:

. ■

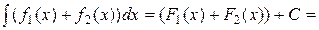
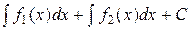В силу определения интеграла и равенства 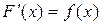из каждой формулы таблицы производных получится соответствующая формула для вычисления неопределённого интеграла.

Таблица интегралов

1. ;

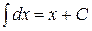2. , ;

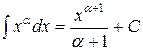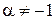3. , ;

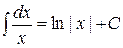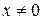4. , ;

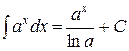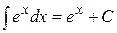5. ;

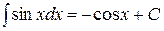6. ;

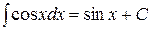7. ;

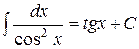8. ;

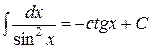9. ;

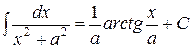10. , ;

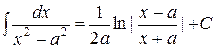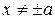11. ;

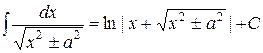12. 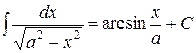; -a<x<a.

Справедливость этих формул проверяется непосредственно дифференцированием правой части. Эти интегралы называются табличными. Интегралы от более сложных функций находятся с помощью свойств интегралов и таблицы интегралов.

Замечание.В теории дифференцирования функций было установлено, что производная любой элементарной функции тоже представляет элементарную функцию, т.е. применение операции дифференцирования не выводит из класса элементарных функций. С операцией интегрирования сложнее. Интегралы от некоторых элементарных функций не выражаются через элементарные функции, т.е. не являются элементарными. Например,

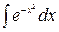- интеграл Пуассона;

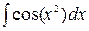
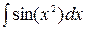- интегралы Френеля;

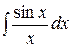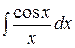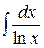; ; интегральные синус, косинус, логарифм.

Эти интегралы называют специальными функциями. Они часто используются в различных разделах физики и других дисциплинах. Для них составлены таблицы, графики, компьютерные программы.

Несобственные интегралы

ГЛАВА 6. ИНТЕГРАЛЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ