Физический смысл поверхностного интеграла 2-го рода.

Сравнив формулы (13.9) и (13.1), увидим, что поверхностный интеграл 2-го рода представляет собой поток векторного поля 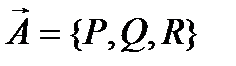через выбранную сторону поверхности S. При этом из формулы (13.9) следует, что поток можно задать и в виде поверхностного интеграла 1-го рода вида (13.5).

40. Поток векторного поля. Вывод формулы для его исчесления.

Пусть векторное поле образовано вектором .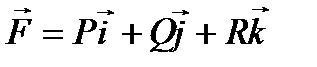

Рис. 29

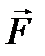Для наглядности будем считать - вектором скорости некоторого потока жидкости, движущейся стационарно. Представим, что некоторая поверхность S находиться в этом потоке и пропускает жидкость. Требуется вычислить, какое количество жидкости протекает через поверхность S (рис. 29).

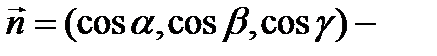единичный вектор нормали к рассматриваемой стороне поверхности S.

Потоком вектора 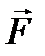через поверхность S называется интеграл П= 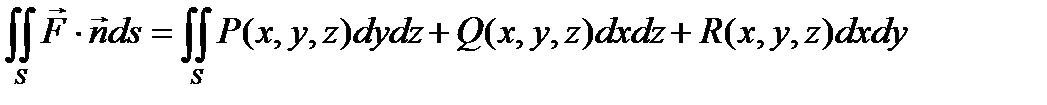- (этот интеграл ещё называют поверхностным интегралом II-го рода, 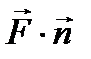- скалярное произведение)

Поток П вектора 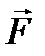есть скалярная величина, равная объему жидкости, которая протекает через поверхность S за единицу времени. В общем случае, поток поля вектора 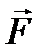пропорционален числу векторных линий, пронизывающих поверхность.

Т.О. если мы рассматриваем графическое изображение векторного поля, то можно судить о величине потока через одинаковые площадки по густоте векторных линий – там, где линии расположены ближе друг к другу, там больше и величина потока.

Рис. 30

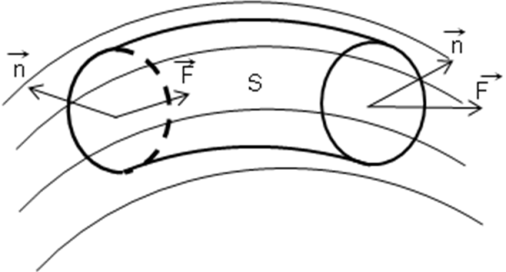Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объём V (рис. 30). Тогда поток вектора записывается в виде П= 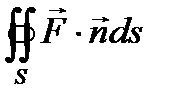. Если векторное поле 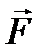- поле скоростей текущей жидкости, то величина потока П через замкнутую поверхность дает разность между количеством жидкости, вытекающей из области V и втекающей в неё за единицу времени.

Если П>0, то из области V вытекает больше жидкости, чем в неё втекает. Это значит, что внутри области имеются дополнительные источники. Если П<0, то внутри области V имеются стоки, поглощающие жидкость.

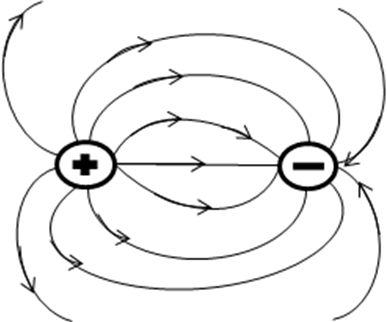Можно сказать, что источники – точки, откуда векторные линии начинаются, а стоки – точки, где векторные линии кончаются. Так в электростатическом поле источником является положительный заряд, стоком отрицательный заряд магнита (рис. 31).

Рис. 31

Если П=0, то из области V вытекает столько же жидкости, сколько в неё втекает в единицу времени; внутри области либо нет ни источников ни стоков, либо они таковы, что их действие взаимно компенсируется.

41. Формула Остроградского – Гаусса

Если функции 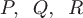дифференцируемы в замкнутой области 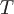, ограниченной кусочно-гладкой поверхностью 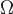, то имеет место формула Остроградского-Гаусса

,

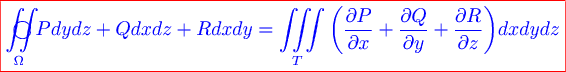где выбрана внешняя сторона поверхности .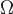

Для векторного поля 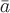в области 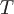существует дивергенция, вычисляемая по формуле

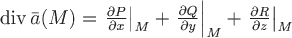
в любой точке .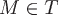

Тогда формула Остроградского-Гаусса в векторной форме имеет вид

.

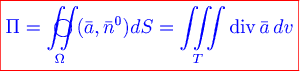Теорема. Поток вектора 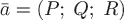через внешнюю сторону замкнутой поверхности 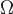равен тройному интегралу от дивергенции 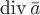по области 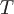, ограниченной поверхностью .

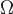Следствие 1.Если для векторного поля 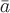дивергенция равна нуль, т.е. 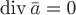, то поток вектора 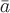через любую замкнутую поверхность равен нулю.

Следствие 2. Пусть в точке 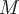имеется изолированный источник или сток, т.е. 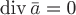всюду в поле, кроме самой точки 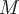. Тогда поток вектора 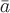через замкнутую поверхность 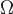, содержащую внутри себя точку 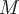, не зависит от формы поверхности.

42. Дивергенция векторного поля, ее свойства. Соленоидальные векторные поля.

Дивергенция - численная характеристика плотности источника или стока поля в данной точке.

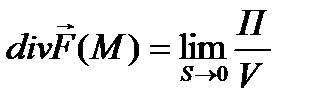- предел отношения потока поля через некоторую замкнутую поверхность к объёму, ограниченному этой поверхностью, когда поверхность S (рис. 30) стягивается в точку М, называется дивергенцией поля в точке М.

Если 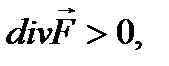то в точке М иметься источник поля плотности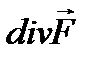

Если 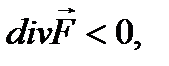то в точке М сток плотности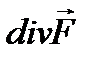

Если 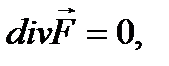то в точке М нет источников и нет стоков.

Дивергенция характеризирует мощность (интенсивность) источника или стока.

Формула для вычисления дивергенции:

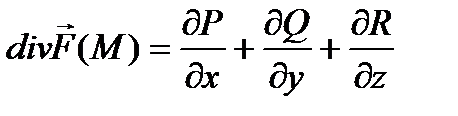
Соленоидальное поле.

Поле вектора 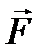называется соленоидальным или трубчатым, если во всех его точках дивергенция поля равно нулю: div 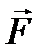=0 (нет источников и стоков).

Отличительная особенность соленоидального поля состоит в том, что в таком поле векторные линии нигде не кончаются и нигде не начинаются. Они уходят в бесконечность или замыкаются. Поле электрической напряженности точечного заряда является соленоидальным, векторными линиями являются лучи, выходящие из точки размещения заряда и уходящие в бесконечность.

В соленоидальном поле поток вектора через любую замкнутую поверхность равен нулю, а поток соленоидального поля через любое поперечное сечение векторной трубки имеет одно и то же значение, называющееся интенсивностью трубки.

43. Формула Грина. Вычисление площади плоской фигуры с помощью криволинейного интеграла. Формулировка теоремы Стокса

Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция

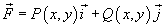
с непрерывными частными производными первого порядка 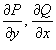. Тогда справедлива формула Грина

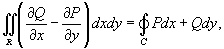Если 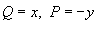, то формула Грина принимает вид

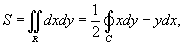
где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией

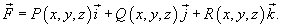
Ротором или вихрем векторного поля 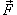называется вектор, обозначаемы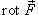й или 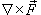и равный

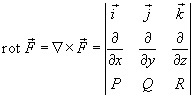
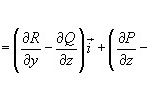
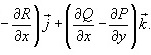
Формула Грина в векторной форме записывается в виде

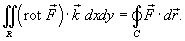18)