Вычисление криволинейных интегралов второго рода

Явное представление кривой интегрирования.

Если плоская кривая АВ задана уравнением 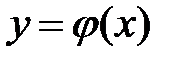, , 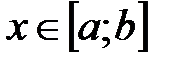где функция 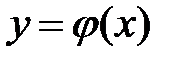и ее производная 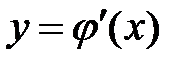непрерывны на отрезке 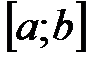, то криволинейный интеграл вычисляется по формуле .

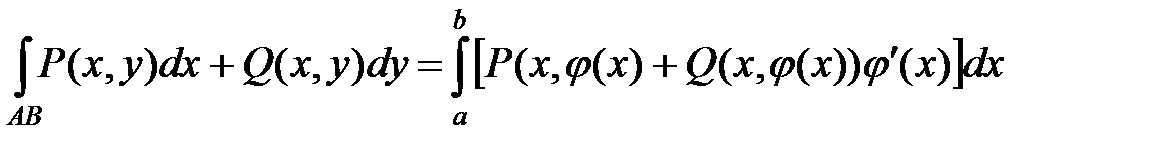Параметрическое представление кривой интегрирования.

Пусть кривая АВ задана параметрическими уравнениями x=x(t) и y=y(t), где функции x(t) и y(t) непрерывны вместе с производными на отрезке 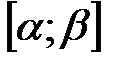, причем начальной точке А соответствует значение параметра t=α, конечной точке В значение t=β. Криволинейный интеграл вычисляется по формуле

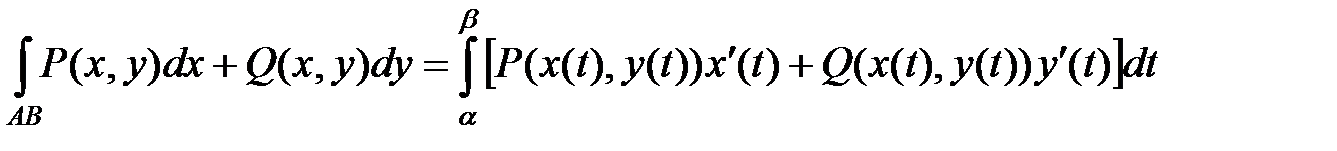
Пример.

Вычислить криволинейный интеграл 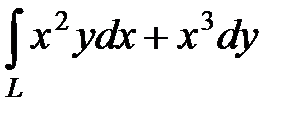. L – контур, ограниченный параболами 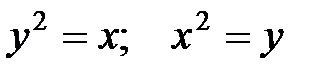(рис. 23). Направление обхода контура положительное, т.е против движения часовой стрелки.

Рис. 23

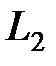Представим замкнутый контур L как сумму двух дуг L₁ и . На дуге L₁ 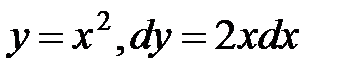, х изменяется от 0 до 1,ана дуге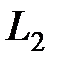 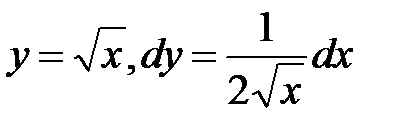, х изменяется от 1 до 0.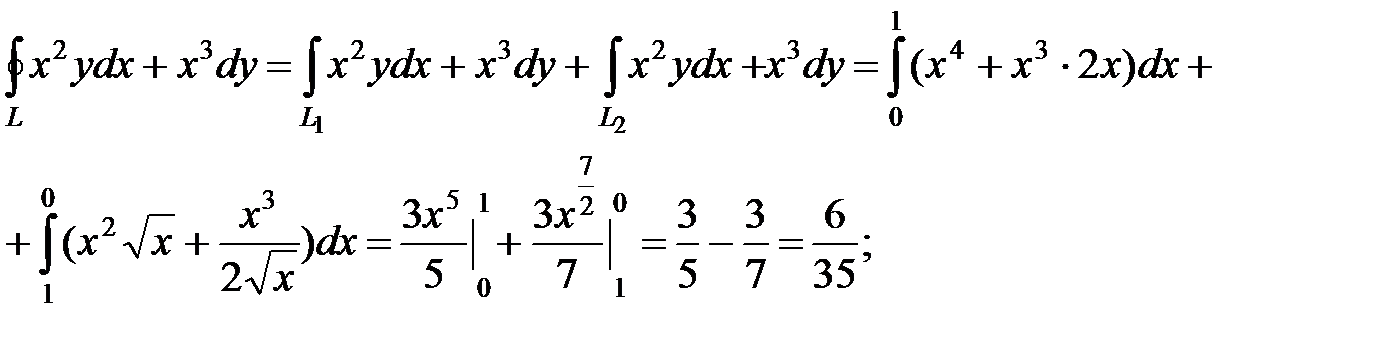

38. Потенциальные векторные поля. Необходимые и достаточные условия потенциальности векторного поля. Нахождение потенциала.

Векторное поле 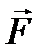называется потенциальным (или безвихревым или градиентным), если во всех точках поля ротор равен нулю, .

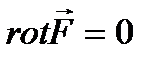Основные свойства потенциального поля:

1) Циркуляция потенциального поля 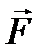по любому замкнутому контуру в этом поле равна нулю.

Для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю; в поле скоростей текущей жидкости, равенство Ц=0 означает, что в потоке нет замкнутых струй, т.е. нет водоворотов. В потенциальном поле отсутствуют вихри.

2) В потенциальном поле 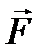криволинейный интеграл 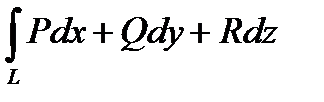вдоль любой кривой L с началом в точке 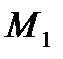и концом в точке 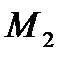зависит только от положения точек 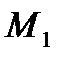и 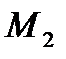и не зависит от формы кривой.

3) Потенциальное поле является полем градиента некоторой скалярной функции U(x,y,z), т.е. если 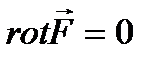, то функция U(x,y,z) такая, что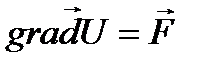

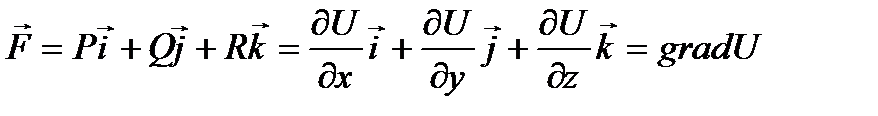
Потенциальное поле определяется заданием одной скалярной функции

U=U(x,y,z) – его потенциал.

Потенциал векторного поля может быть найден по формуле

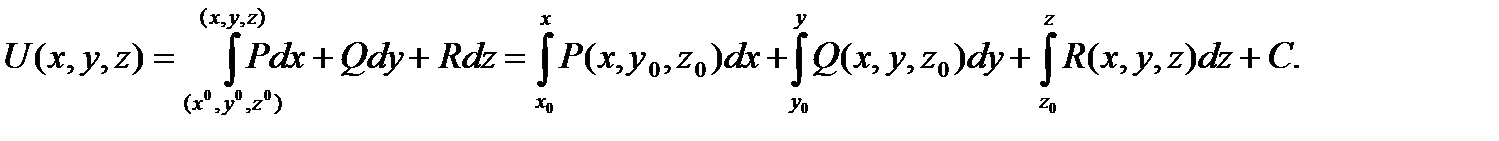
Пример: Установить потенциальность поля 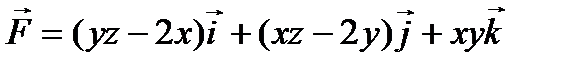и найти его потенциал.

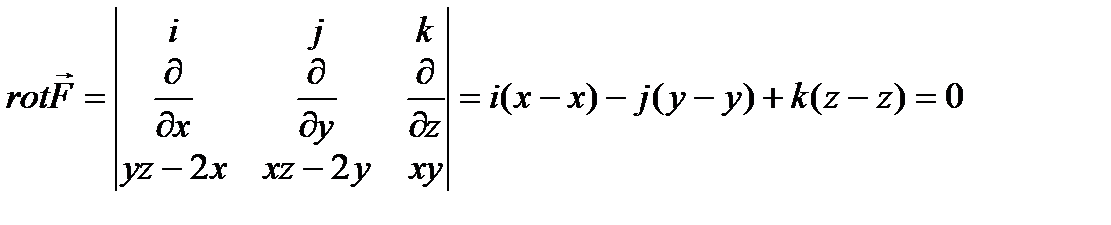
В качестве фиксированной точки (х₀, y₀, z₀) возьмем точку (0;0;0)

U(x,y,z)=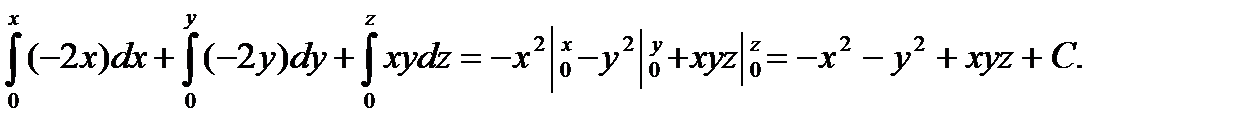

Примером потенциального поля является электрическое поле напряженности 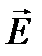точечного заряда q.

39. Поверхностный интеграл 2-го рода, его определение, свойства. Вычисления и связь с поверхностным интегралом 1- го рода.

Введем определение поверхностного интеграла 2-го рода по аналогии с соответ-ствующим криволинейным интегралом. Рассмотрим гладкую двустороннюю поверхность S, заданную уравнением z = z(x, y), в каждой точке которой определена функция f(M) = f(x, y, z), и выберем какую-либо из ее сторон (или, что то же самое, определенную ориентацию). Разобьем поверхность S на части S₁, S₂,…, S_п, выберем в каждой части S_i точку M_i(x_i, y_i, z_i), и умножим f(M_i) на площадь D_i проекции части S_i на плоскость Оху. При этом будем считать, проекция части верхней по отношению к плоскости Оху стороны рассматриваемой поверхности имеет знак «+», а нижней – знак «-». Составим сумму

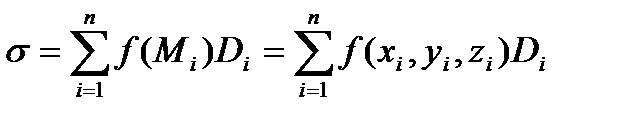. (13.2)

Определение 13.4. Если существует конечный предел суммы (13.2) при ρ→0, не зависящий от способа разбиения поверхности и выбора точек на ней, то он называет-ся поверхностным интегралом второго рода от функции f(M) по выбранной сто-роне поверхности S и обозначается

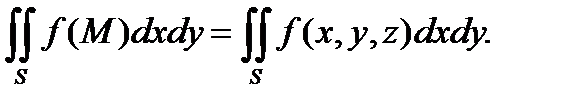(13.3)

Замечание. В этой символической записи не содержится указания на то, какая сторона поверхности выбрана, поэтому это требуется оговаривать отдельно.

Подобным образом можно проектировать части поверхности на координатные плос-кости Оxz и Оyz (при условии, что уравнение поверхности можно представить в виде y = y(x, z) или x = x(y, z) ). Получим два других поверхностных интеграла 2-го рода:

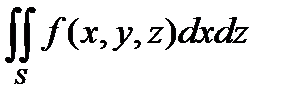и 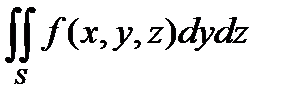. (13.4)

Рассмотрев сумму интегралов вида (13.3) и (13.4) по одной и той же поверхности соответственно от функций P(x, y, z), Q(x, y, z), R(x, y, z), получим поверхностный интеграл второго рода общего вида:

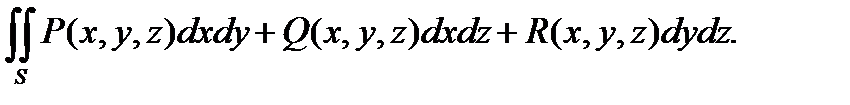(13.5)

Отметим основное свойство поверхностного интеграла 2-го рода:

При замене рассматриваемой стороны поверхности на противоположную поверхностный интеграл 2-го рода меняет знак: 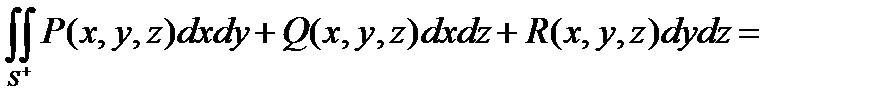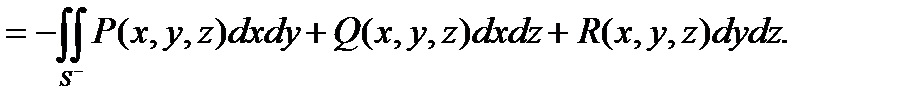(13.6) Справедливость этого утверждения следует из определения 13.4.