Сферическая система координат.

Сферическими координатами точки М(x;y;z) в пространстве Оxyz называется тройка чисел ρ, φ, θ, где ρ - длина радиус-вектора проекции точки М, φ - угол, образованный проекцией радиуса-вектора 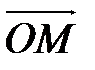на плоскость Оxy и осью Ох, θ – угол отклонения радиуса- вектора 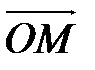от оси Оz (рис. 20).

z

М

r

θ

0 φ x

Рис. 20

y

Связь координат произвольной точки М пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

( )

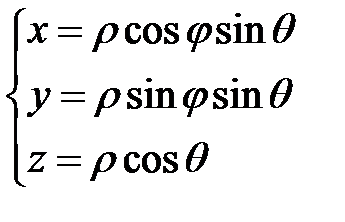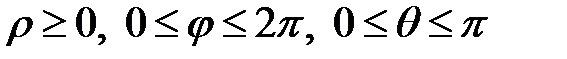В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам.

Для представления тройного интеграла в сферических координатах вычисляем якобиан:

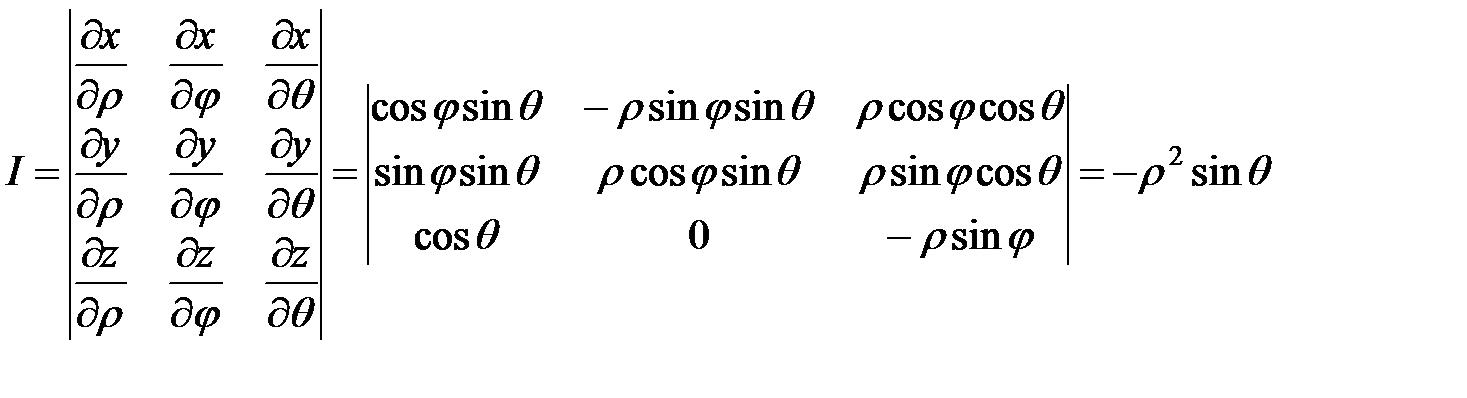
Окончательно получаем:

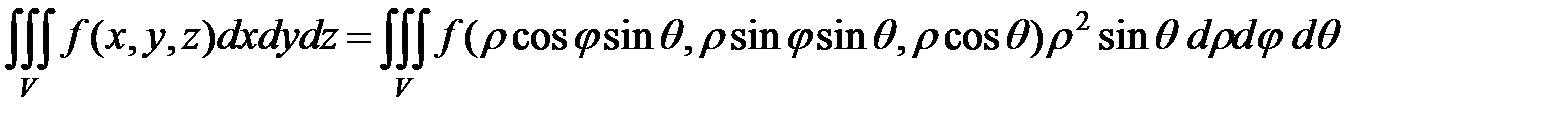, где

, , , .

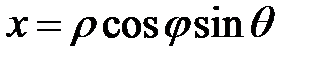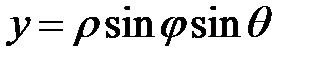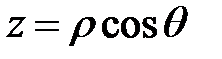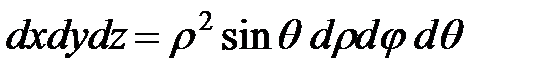Замечание: переходить к сферическим координатам удобно, когда область интегрирования V есть шар (уравнение его границы 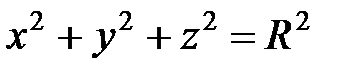в сферических координатах имеет вид 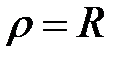) или его часть, а также если подынтегральная функция имеет вид .

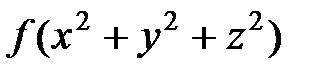31 геометрические приложения кратных интегралов (объем тела, площадь поверхности)

1) Площадь плоской области S:

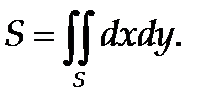(11)

Объем тела.

Объем области выражается формулой

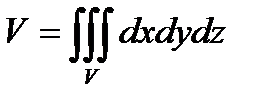- в декартовых координатах,

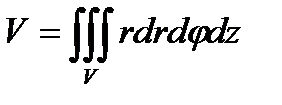- в цилиндрических координатах,

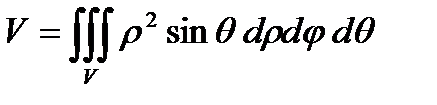- в сферических координатах.

Масса тела.

Масса тела при заданной объемной плотности μ вычисляется с помощью тройного интеграла .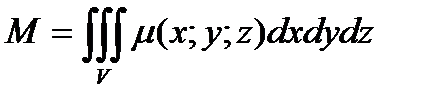

Статические моменты.

Моменты 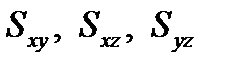тела относительно координатных плоскостей Oxy, Oxz, Oyz вычисляются по формулам

.

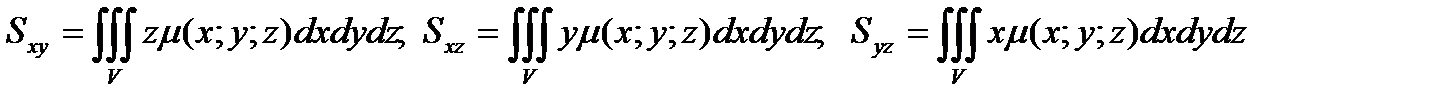Центр тяжести тела.

Координаты центра тяжести тела V находятся по формулам

.

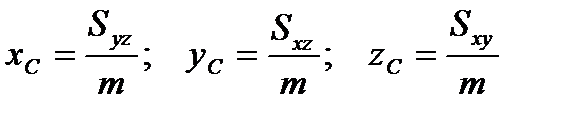32 Вычисление криволинейных и поверхностных интегралов 1-го рода

Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части Δs_i длиной Δs_i и выберем на каждой из частей точку M_i. Назовем d длину наибольшего отрезка кривой: .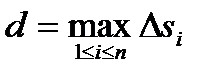

Криволинейным интегралом первого родаот функции f по кривой L называется предел интегральной суммы 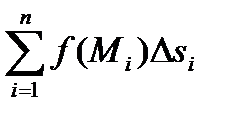, не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек M_i:

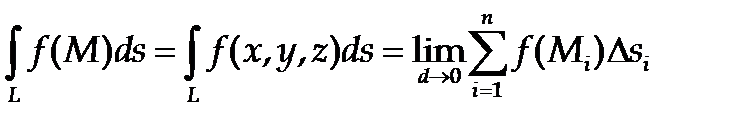(24)

Если кривую L можно задать параметрически:

x = φ(t), y = ψ(t), z = χ(t), t₀ ≤ t ≤ T,

то способ вычисления криволинейного интеграла первого рода задается формулой

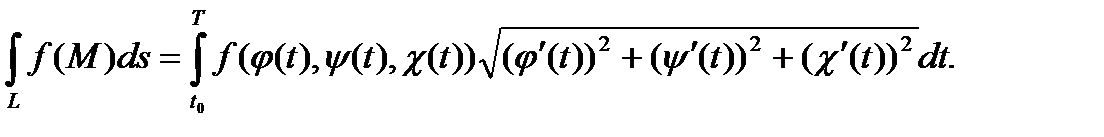(25)

В частности, если кривая L задана на плоскости явным образом:

у=φ(х), где х₁ ≤ х ≤ х₂, формула (40) преобразуется к виду:

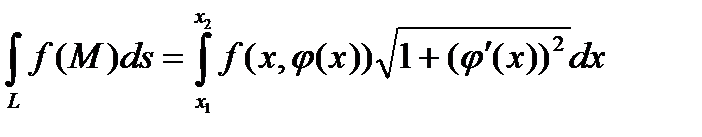. (26)

Теперь умножим значение функции в точке M_i не на длину i-го отрезка, а на проекцию этого отрезка, скажем, на ось Ох, то есть на разность x_i – x_i-1 = Δx_i.

Рассмотрим некоторую поверхность S, ограниченную контуром L, и разобьем ее на части S₁, S₂,…, S_п (при этом площадь каждой части тоже обозначим S_п). Пусть в каждой точке этой поверхности задано значение функции f(x, y, z). Выберем в каждой части S_i точку

M_i (x_i, y_i, z_i) и составим интегральную сумму

.

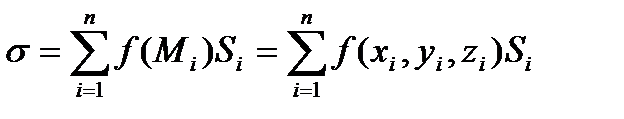Если существует конечный предел при 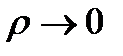этой интегральной суммы, не зависящий от способа разбиения поверхности на части и выбора точек M_i, то он называется поверхностным интегралом первого рода от функции f(M) = f(x, y, z) по поверхности S и обозначается

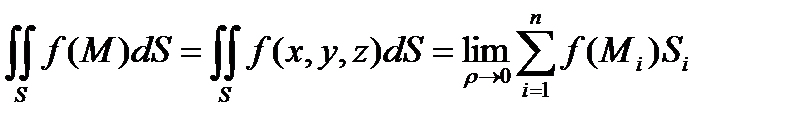. (32)

Если поверхность S задается явным образом, то есть уравнением вида z = φ(x, y), вычисление поверхностного интеграла 1-го рода сводится к вычислению двойного интеграла:

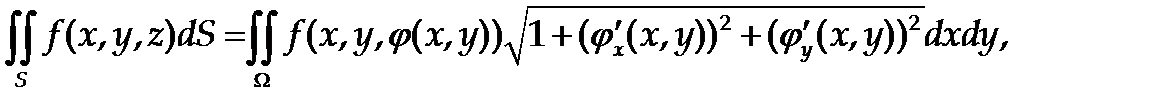(33)

где Ω – проекция поверхности S на плоскость Оху.

33. Механические приложения кратных интегралов, и поверхностных интегралов 1-го рода

1) Длина кривой.

Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:

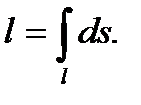(39)

2) Масса кривой.

Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле

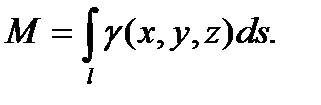(40)

34. Скалярное поле. Поверхности (линии). Производная по направлению. Градиент скалярного поля, его связь с производной по направлению. Основные свойства градиента.

Скалярным полем называется область пространства, если каждой точке М этой области соответствует определенное число U(М).

Другими словами: если в пространстве (х, y, z) имеется область D, в которой задана функция U=U(x,y,z), то говорят, что в области D задано скалярное поле.

Пример:

1) если U(x,y,z) – обозначает температуру в точке М, то говорят, что задано скалярное поле температур: в некоторой декартовой системе координат находится неравномерно нагретое тело и температура его в каждой точке М(x,y,z) известна t˚=U(M). Тогда часть пространства, занятая телом, будет скалярным полем температур данного тела;

2) скалярное поле атмосферного давления, плотности (массы, воздуха), поле влажности;

3) скалярное поле солености воды (устье реки впадающей в море).

Если скалярная величина U(M) не зависит от времени то поле называется стационарным (или установившимся).

Поле, которое меняется с течением времени, называется нестационарным.

Пример: поле температуры при охлаждении тела, поле влажности – нестационарное поле, поле плотности данного тела – стационарное.

Если функция зависит только от двух координат x и y, то поле функции U(M)=U(x,y) называется плоскопараллельным.

Поверхности и линии уровня.

Рассмотрим скалярное поле, задаваемое функцией U=U(x,y,z).

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U(M) принимает постоянное значение, т.е. U(x,y,z)=C (C – const).

Часто такие поверхности называются изоповерхностями.

Давая в уравнении U(x,y,z)=C величине C различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку проходит только одна поверхность уровня.

Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой круговые цилиндры, общей осью которых служит нить.

В случае плоского поля U=U(x,y,z) равенство U(x,y)=С представляет собой уравнение линии уровня (изолинии).

На различных картах и схемах можно найти разнообразные изолинии - линии равных глубин или высот на географических картах, линии равного давления – изобары, линии равной температуры – изотермы на метеорологических картах.

Пример: 1) Для скалярного поля U= 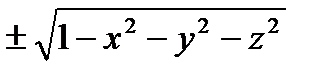поверхностями уровня является множество концентрических сфер с центром в начале координат

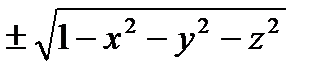=С

2) Дано скалярное поле 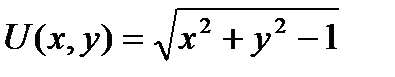. Построить линии уровня.

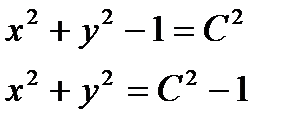
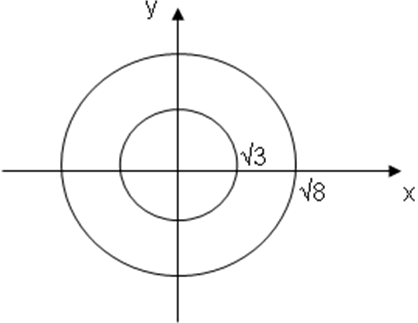
С=1 - точка (0;0)

С=2 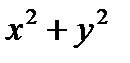=3 - окружность с радиусом 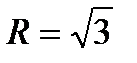и центром С(0;0)

Рис. 26

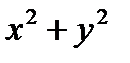С=3 =8 - окружность с радиусом 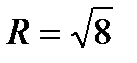и центром С(0;0) (рис. 26)

Производная по направлению.

Для характеристики скорости изменения поля U=U(M) в заданном направлении введем понятие “производной по направлению”.

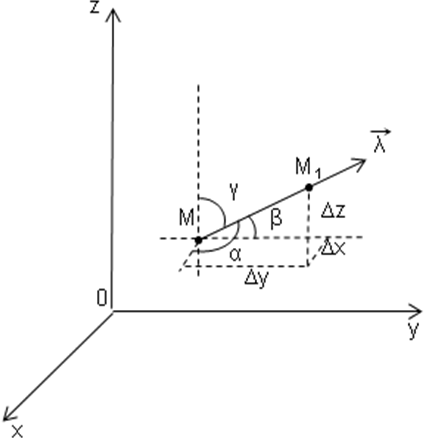
Возьмем в пространстве, где задано поле U=U(x,y,z) некоторую точку М и найдем скорость изменения функции при движении точки М в произвольном направлении 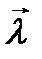(рис.27).

Пусть вектор 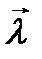имеет начало в точке М и направляющие косинусы cosα, cosβ, cosγ.

Приращение функции U возникающее при переходе от точки М к точке 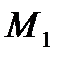в направлении вектора 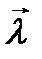определится как разность значений функции U в точках М и М₁

Рис. 27

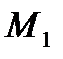∆U=U( )-U(M) или ∆U=U(x+∆x,y+∆y,z+∆z), тогда ∆λ = .

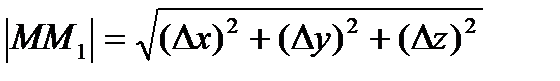Производной от функции U=U(x,y,z) в точке М по направлению 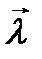называется предел

Рис. 27

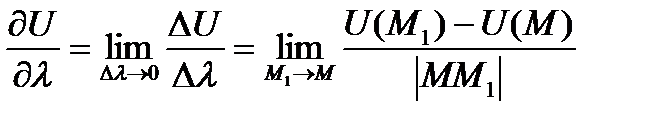
Производная по направлению 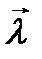характеризует скорость изменения функции в точке М по этому направлению.

Если 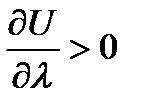, то функция возрастает в этом направлении, если 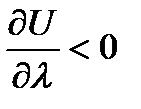- убывает в направлении 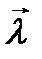. Кроме того модуль 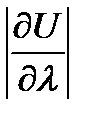представляет величину мгновенной скорости изменения функции U в направлении 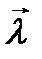в точке М. Чем больше 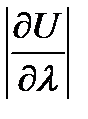, тем быстрее изменяется функция U. В этом состоит физический смысл производной по направлению.

Если функция U(x,y,z) дифференцируема в точке М, то производная по направлению 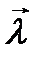= 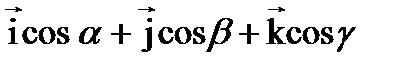существует и находиться по формуле:

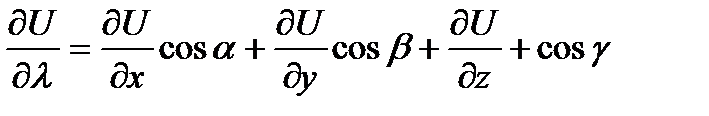(3.1.1)

Замечание: понятие производной по направлению является обобщением понятия частных производных 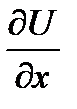, , 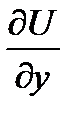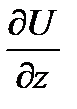. Их можно рассчитать как производные от функции F по направлению координатных осей Оx, Оy, Оz. Так, если 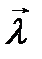совпадает с положительным направлением оси Ох, то 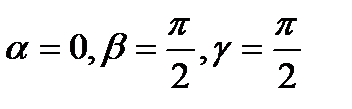. Получаем .

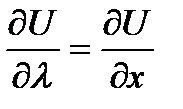Пример:

Найти производную функции 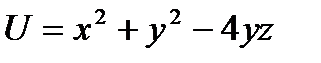в точке 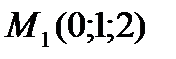в направлении от этой точки к точке .

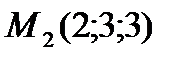Решение:

Находим вектор 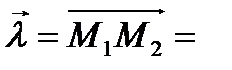{2;2;1} и направляющие косинусы:

, , .

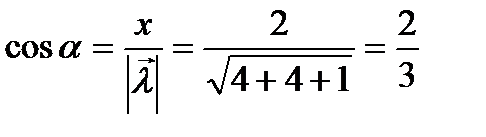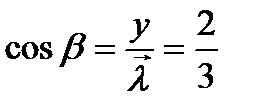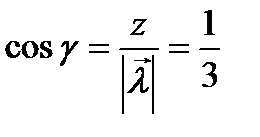Находим частные производные:

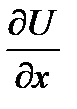=2х, 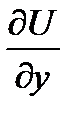=2у-4z, 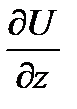= -4y.

.

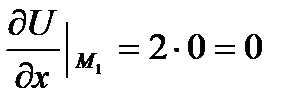
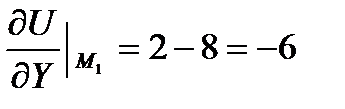
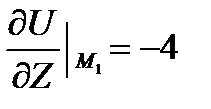Находим производную по направлению 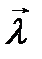по формуле (3.1.1)

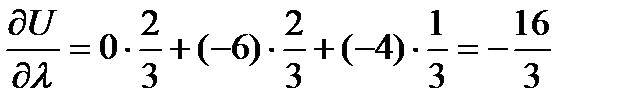
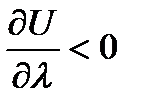функция в данном направлении убывает.

Градиент скалярного поля.

В каком направлении 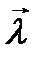производная 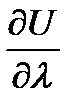имеет наибольшее значение?

Можно заметить, что правая часть формулы для вычисления производной по направлению представляет собой скалярное произведение единичного вектора 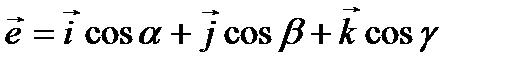и некоторого вектора .

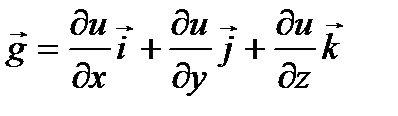Вектор, координатами которого являются значения частных производных функций поля U(x,y,z) в любой точке M(x,y,z) называют градиентом функции и обозначают .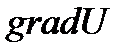

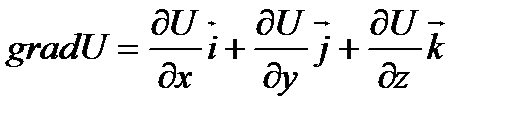(3.1.2)
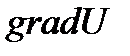- величина векторная!

Свойства градиента:

1) градиент функции указывает направление наибыстрейшего возрастания функции.

Формулу (3.1.2) можно переписать в виде:

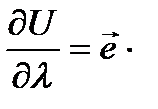
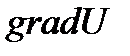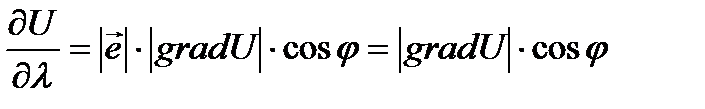, , (3.1.3)

где 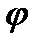- угол между вектором 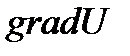и направлением .

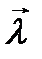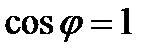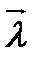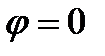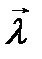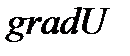Из формулы (3.1.3) видно, если , то производная по направлению достигает максимального значения, а это значит , т.е. векторы и - совпадают.

2) наибольшая скорость изменения функции U в точке M равна

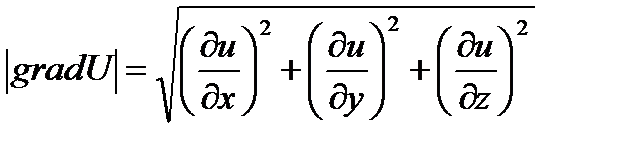
3) градиент направлен по нормали к поверхности уровня, проходящей через данную тучку в сторону возрастания функции.

4) единичный вектор нормали к поверхности уровня может быть вычислен как

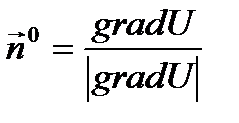
Пример:

Найти скорость наибыстрейшего возрастания поля U=xyz в т. Р(1;2;-2)

Решение:

Скорость наибыстрейшего возрастания функции в точке равна модулю градиента в этой точке.

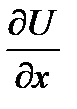=yz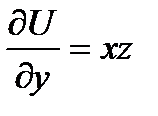

.

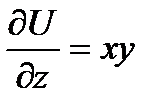
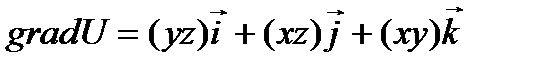
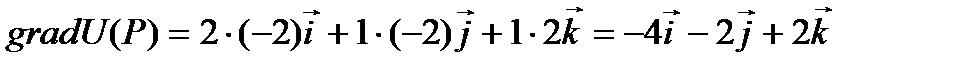
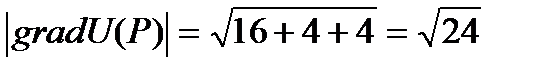Отметим, что функция U будет убывать с наибольшей скоростью 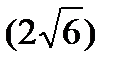, если точка P движется в направлении антиградиента .

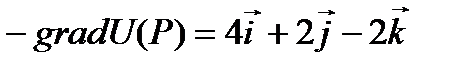35. векторная функция скалярного аргумента, ее предел, непрерывность, производная и дифференциал.

Векторназывается векторной функцией скалярного аргумента, если каждому значению скаляра из области допустимых значений соответствует определенное значение вектора:

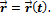
Вектор

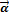
называется бесконечно малым, если его модуль стремится к нулю.

Производной векторной функции по ее скалярномуаргументуназывается предел отношения приращения вектора к соответствующему приращению аргумента, когда это приращение стремится к нулю:

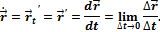
Некоторые правила дифференцирования векторной функции по скалярному аргументу:

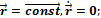
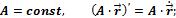
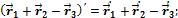
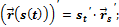
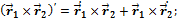
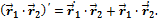
Докажем справедливость последнего правила.

Пусть

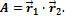
Если скалярному аргументу

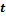
дать приращение

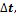
то векторные функции

получат приращения

соответственно. При этом

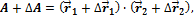
откуда

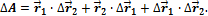
Поделим обе части этого равенства на

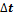
и перейдем к пределу при

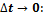
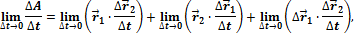
откуда и следует, что доказываемое правило справедливо.

Применительно к векторной функции скалярного аргумента рассматриваются также дифференциал

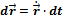
и интегралы, в частности определенный интеграл

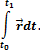
Если векторную функцию скалярного аргумента рассматривать в декартовой системе координат, то

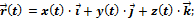
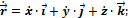
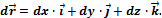
36. Векторное поле. Работа векторного поля, вывод формул для его исчисления.

Если каждой точке М области пространства соответствует некоторый вектор 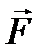, то говорят, что задано векторное поле.

Векторным полем называется область пространства или плоскости, каждой точке которой М(x,y,z) поставлен в соответствие вектор :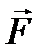

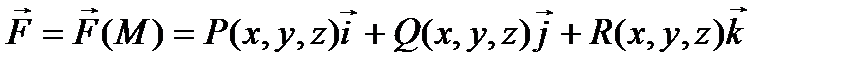, где P(x, y, z), Q(x, y, z) и R(x, y, z) – некоторые функции.

Если поле задано на плоскости, то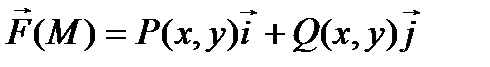

Примерами векторных полей являются: поле силы тяжести; поле скоростей частиц текущей жидкости (ветра); магнитное поле; поле напряженностей заряженных объектов и т.д.

Векторное поле называется однородным, если 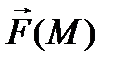- постоянный вектор, т.е. P,Q,R – постоянные величины.

Таким полем является поле тяжести. Здесь . P=0, Q=0, R=-mg, g - ускорение силы тяжести, m – масса точки.

Векторной линией поля вектора 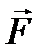называется такая линия, в каждой точке которой вектор поля направлен по касательной к этой линии.

Для определения уравнения векторных линий поля 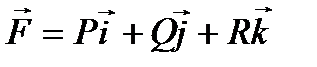следует решить систему дифференциальных уравнений .

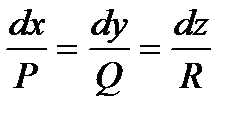Для плоского поля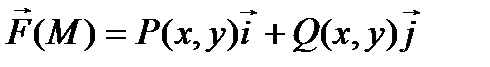

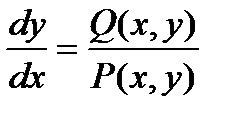
Пример: векторное поле задано вектором 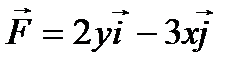. Найти векторные линии, изобразить их и на одной из них построить три вектора.

Решение: составляем дифференциальное уравнение 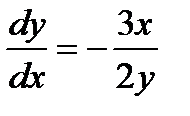. Это уравнение с разделяющимися переменными. Решаем его и находим уравнения векторных линий.

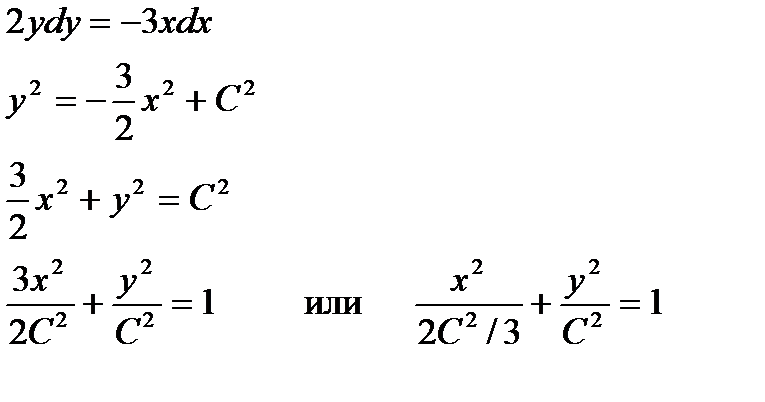
Дадим константе С несколько различных числовых значений :

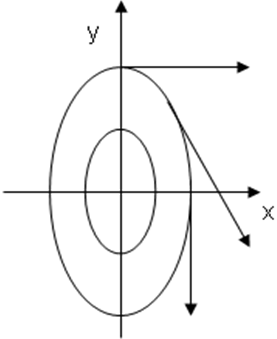С=3 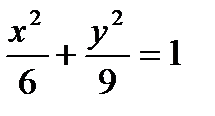- эллипс ( 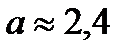, b=3);

С=5 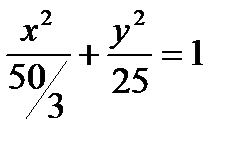- эллипс ( 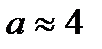, b=5).

На линии 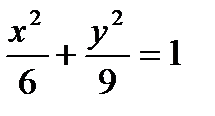построим три вектора (рис. 28)

Рис. 28

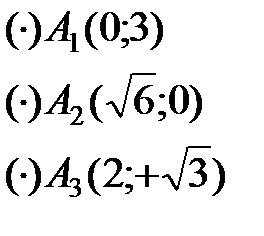
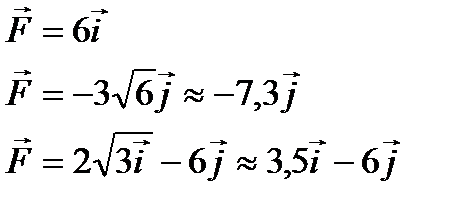
В силовых полях векторные линии - это силовые линии, в поле скоростей текущей жидкости векторными линиями будут линии, по которым движутся частицы жидкости (линии тока), для магнитного поля векторными линиями будут линии, выходящие из северного полюса, и оканчивающееся в южном.

Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называются векторной трубкой.

37. Криволинейный интеграл второго рода, его определение, свойства. Вычисления и связь с криволинейным интегралом 1- го рода.

Криволинейные интегралы второго рода. Основные понятия

A •

•

𝑥𝑖-1

𝑥𝑖

𝑦 𝑖+1

𝑦𝑖-1

𝑀𝑖-1

𝑀𝑖

𝐶𝑖

B

𝑥

y

𝐹

⃗

η𝑖

ξ𝑖

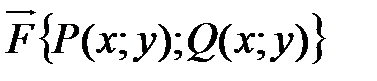Рассмотрим задачу: На материальную точку (x;y) действует переменная сила . Под действием этой силы точка перемещается по некоторой кривой АВ (от точки А к точке В). Найти работу, которую производит сила на данном участке.

Решение.

Рис. 22

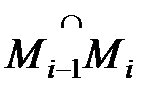Разобьем кривую АВ на n частей точками М₀=А, М₁, …, М_i-1, M_i, …M_n=B. На каждой «элементарной дуге» возьмем произвольным образом точку 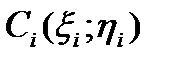(рис. 22). Заменим каждую дугу 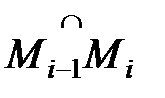вектором 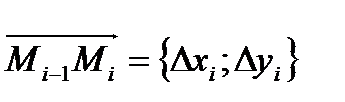, где 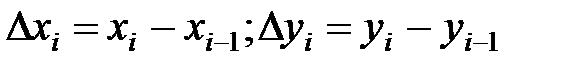. Силу F_i будем считать постоянной на векторе перемещения и равной заданной силе в точке С_i дуги 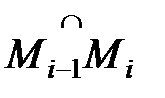, т.е. .

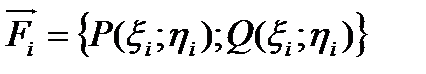Работа есть скалярное произведение вектора силы и вектора перемещения.

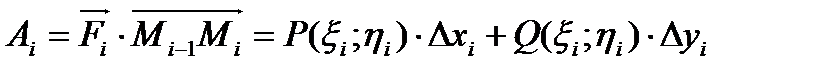- работа на i-ом участке. Работа на всей кривой будет равна сумме работ на i-ых участках, т.е. .

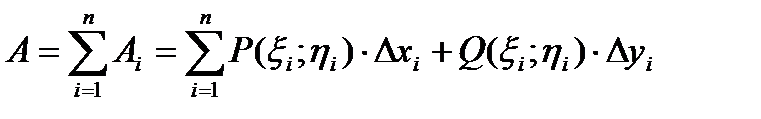За точное значение работы А примем предел полученной суммы

.

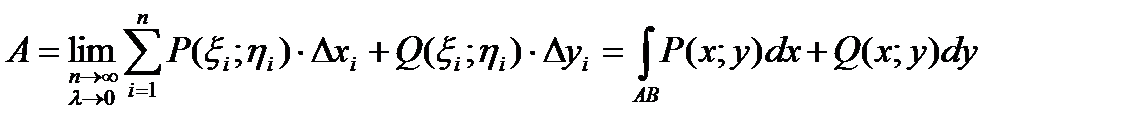Таким образом, работу можно вычислить, проинтегрировав вектор силы по дуге перемещения. Отвлекаясь от физического смысла интеграла, если при стремлении к нулю шага разбиения кривой АВ интегральные суммы имеют конечный предел, то этот предел называется криволинейным интегралом II рода(или интегралом по координатам) и обозначается

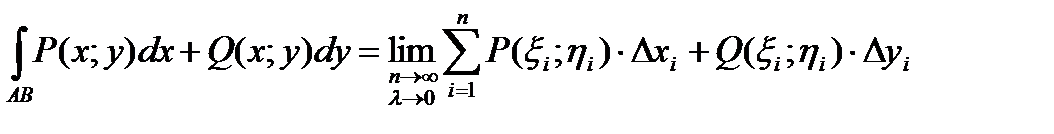
Аналогично определяется криволинейный интеграл по пространственной кривой L

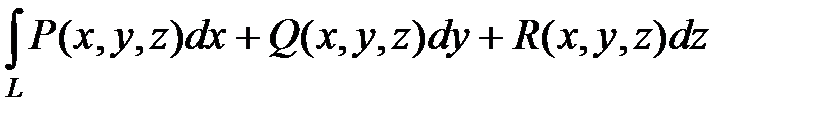
Теорема. Если кривая АВ – кусочно-гладкая, а функции P(x, y, z), Q(x, y, z) и R(x, y, z) – непрерывны на кривой АВ, то криволинейный интеграл II рода 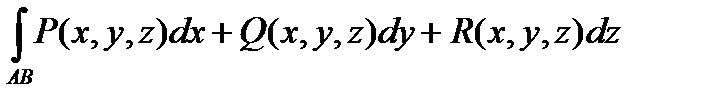существует и не зависит от способа разбиения и выбора точки.

Свойства криволинейного интеграла второго рода.

1) Криволинейный интеграл при перемене направления пути интегрирования кривой меняет знак.

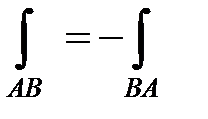
2) Если кривая АВ точкой С разбита на части АС и СВ, то интеграл по всей кривой равен сумме интегралов по ее частям

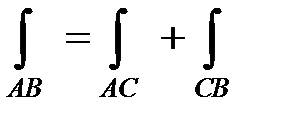
3) Если кривая АВ лежит в плоскости, перпендикулярной оси Ох, то

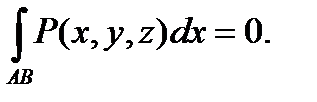
Аналогичные соотношения справедливы при интегрировании для кривой, лежащей в плоскости, перпендикулярной оси Oy или оси Oz ;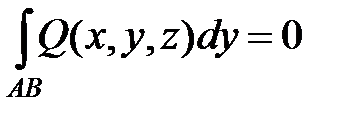

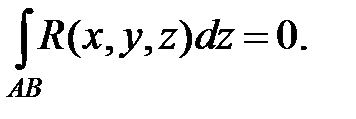
4) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой (обозначается )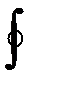

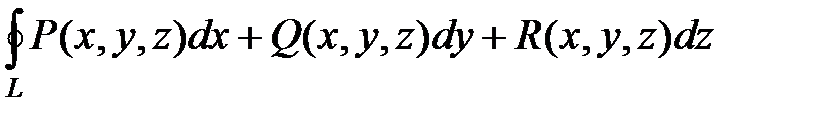
Направление обхода контура L задается дополнительно. Если L – замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным.