Вычисление тройного интеграла в декартовых координатах

z

y

00

x

D

z=z2 (x;y)

z=z1 (x;y)

z

y

x

D

z=z2 (x;y)

z=z1 (x;y)

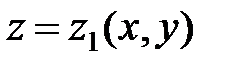Пусть в замкнутой области V пространства Oxyz задана непрерывная функция u=f(x,y,z). Под областью V (рис. 13) понимается замкнутая пространственная область, ограниченная снизу и сверху поверхностями, определенными соответственно уравнениями и 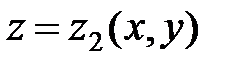( 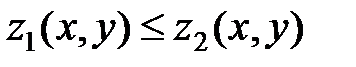), а с боков цилиндрической поверхностью с образующими параллельными оси Оz. В частном случае может оказаться, что образующие цилиндрической поверхности равны нулю (рис. 14).

Рис. 13

Переменные x и y изменяются в плоской области D, которая является проекцией на плоскость xOy пространственной области V.

Рис. 14

Тройной интеграл от функции u=f(x,y,z) записывается так

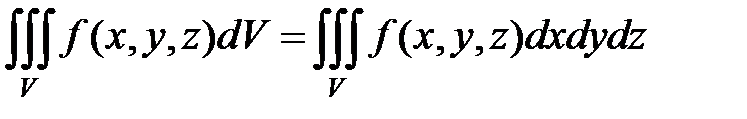
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.

y

х

0

D

y=φ2(x)

y=φ1 (x)

a

b

Если плоская область D ограничена линиям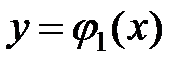и и 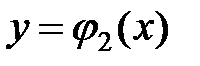( 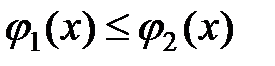) и прямыми х=а и х=b (рис. 15), то тройной интеграл вычисляется по формуле

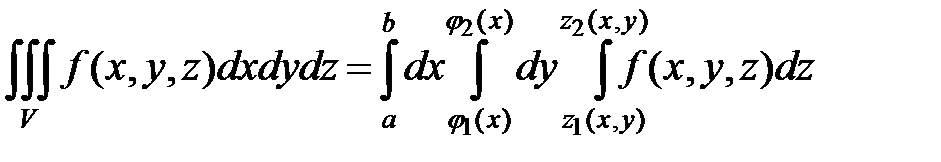(1.6.1)

Рис. 15

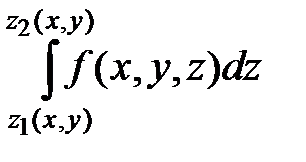При вычислении внутреннего интеграла следует рассматривать переменные x и y как постоянные, единственной переменной величиной при этом является z.

Замечание:

1) порядок интегрирования в формуле (1.6.1) может быть изменен;

2) пределы интегрирования во внешнем интеграле всегда величины постоянные.

28. Отображение плоских и пространственных областей. Якобиан отражения, его геометрический смысл

Пусть функции 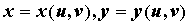взаимно однозначно отображают открытое множество, содержащее область 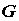плоскости 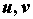на открытое множество, содержащее область 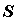, и пусть 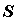является образом 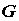. Если 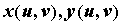и их частные производные непрерывны, а определитель 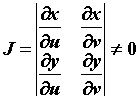, то 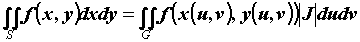. Выражение 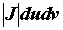называется элементом площади в криволинейных координатах, функциональный определитель 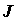- якобианом.

Якобиан, функциональный определитель ½a_ik½₁ⁿ с элементами 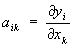, где y_i = f_i(X₁,...,X_n), l £ i £ n, — функции, имеющие непрерывные частные производные в некоторой области А; обозначение:

.

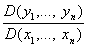Введён К. Якоби (1833, 1841). Если, например, n = 2, то система функций

y₁ = f₁ (. x₁, x₂), y₂ = f₂(x₁, x₂) (1)

задаёт отображение области D, лежащей на плоскости x₁, x₂, на часть плоскости y₁, y₂. Роль Якобиан для этого отображения во многом аналогична роли производной для функции одной переменной. Например, абсолютное значение Якобиан в некоторой точке М равно коэффициенту искажения площадей в этой точке (т. е. пределу отношения площади образа окрестности точки М к площади самой окрестности, когда размеры окрестности стремятся к нулю). Якобиан в точке М положителен, если отображение (1) не меняет ориентации в окрестности точки М, и отрицателен в противоположном случае. Если Якобиан не обращается в нуль в области D и j (y₁, у₂) — функция, заданная в области D₁ (образе D), то

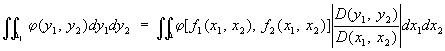
(формула замены переменных в двойном интеграле). Аналогичная формула имеет место для кратных интегралов. Если Якобиан отображения (1) не обращается в нуль в области Д, то существует обратное отображение

x₁ = j₁(y₁, y₂), x₁ = j₂(y₁, y₂),

причём

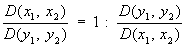
(аналог формулы дифференцирования обратной функции). Это утверждение находит многочисленные применения в теории неявных функций. Для возможности явного выражения в окрестности точки М (x₁⁽⁰⁾,..., x_n⁽⁰, y₁⁽⁰⁾,..., y_m⁽⁰⁾) функций y₁,..., у_т, неявно заданных уравнениями F_k (x₁,..., x_n, y₁,..., у_м) = 0, (2)

1 £ k £ m,

достаточно, чтобы координаты точки М удовлетворяли уравнениям (2), функции Fk имели непрерывные частные производные и Якобиан

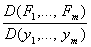
был отличен от нуля в точке М.

29 Замена переменных в двойных интегралах. Двойной интеграл в полярных координатах.