Кинематика вращательного движения

Кинематика вращательного движения

• Часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение, называется механикой. Классическая механика (механика Ньютона-Галилея) изучает законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме.
• Кинематика – раздел механики, предметом изучения которого является движение тел без рассмотрения причин, которыми это движение обусловлено.
• В механике для описания движения тел в зависимости от условий конкретных задач используются различные физические модели: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело.
• Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение. Совокупность тела отсчета, связанной с ним системы координат и синхронизированных между собой часов называется системой отсчета.
• Вектор Δr=r-r₀, проведенный из начального положения движущейся точки в положение ее в данный момент времени называется вектором перемещения. Линия, описываемая движущейся материальной точкой (телом) относительно выбранной системы отсчета называется траекторией движения. В зависимости от формы траектории различают прямолинейное и криволинейное движение. Длина участка траектории, пройденного материальной точкой за данный промежуток времени, называется длиной пути.
• Скорость – это векторная физическая величина, которая характеризует быстроту движения и его направление в данный момент времени. Мгновенная скорость определяется первой производной радиуса-вектора движущейся точки по времени:

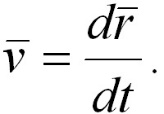
Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Модуль мгновенной скорости материальной точки равен первой производной длины ее пути по времени:

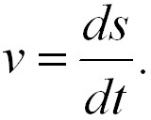
• Ускорение – векторная физическая величина для характеристики неравномерного движения. Она определяет быстроту изменения скорости по модулю и направлению. Мгновенное ускорение - векторная величина, равная первой производной скорости по времени:

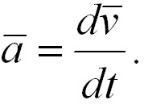
Динамика вращения

Описанное нами движение твердого тела относительно неподвижной точки является основным видом движения. Однако вычислить вектор 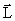– момент импульса системы относительно произвольной точки – не просто: надо знать шесть проекций (три задают положение тела, три задают положение точки).
Значительно проще найти момент импульса 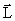тела, вращающегося вокруг неподвижной оси z (рис. 6.4). В этом случае составляющие 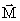– момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления. Вращение вокруг оси z происходит только под действием M_z .

Пусть некоторое тело вращается вокруг оси z (рис. 6.5).

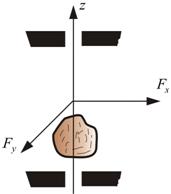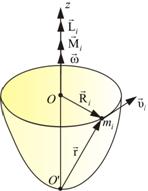Рис. 6.4	Рис. 6.5

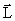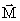Получим уравнение динамики для некоторой точки m_i этого тела, находящегося на расстоянии R_i от оси вращения. При этом помним, что и направлены всегда вдоль оси вращения z, поэтому

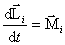или .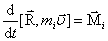

Поскольку 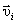у всех точек разная, введем вектор угловой скорости 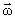, причем 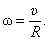. Тогда .
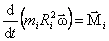Так как тело абсолютно твердое, то в процессе вращения m_i и R_i останутся неизменными. Тогда

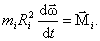
Обозначим I_i – момент инерции точки находящейся на расстоянии R от оси вращения:

.

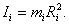(6.2.1)

Момент инерции тела служит мерой инертности во вращательном движении.
В общем случае тело состоит из огромного количества точек, и все они находятся на разных расстояниях от оси вращения. Момент инерции такого тела равен:

.

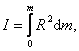(6.2.2)

Кинетическая энергия

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему^[1], энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательного движения^[2].

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[3].

Простым языком, кинетическая энергия — это энергия, которую тело имеет только при движении. Когда тело не движется, кинетическая энергия равна нулю.

Впервые понятие кинетической энергии было введено в трудах Готфрида Лейбница (1695 г.), посвящённых понятию «живой силы» ^[4].

Рассмотрим систему, состоящую из одной материальной точки, и запишем второй закон Ньютона:

{\displaystyle m{\vec {a}}={\vec {F}}.} {\displaystyle {\vec {F}}} — есть равнодействующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение материальной точки {\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} . Учитывая, что {\displaystyle {\vec {a}}={\frac {{\rm {d}}{\vec {v}}}{{\rm {d}}t}}} , получим:

{\displaystyle {\rm {d}}\left({{mv^{2}} \over {2}}\right)={\vec {F}}{\rm {d}}{\vec {s}}.}

Если система замкнута, то есть внешние по отношению к системе силы отсутствуют, или равнодействующая всех сил равна нулю, то {\displaystyle d\left({{mv^{2}} \over {2}}\right)=0} , а величина

{\displaystyle T={{mv^{2}} \over 2}}

остаётся постоянной. Эта величина называется кинетической энергией материальной точки. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

{\displaystyle T={\frac {mv^{2}}{2}}+{\frac {{\mathcal {I}}{\vec {\omega }}^{2}}{2}},}

где:

{\displaystyle \ m} — масса тела

{\displaystyle \ v} — скорость центра масс тела

{\displaystyle {\mathcal {I}}} — момент инерции тела

{\displaystyle {\vec {\omega }}} — угловая скорость тела.

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение её кинетической энергии^.

Механика твердого тела

{\displaystyle \ A_{12}=T_{2}-T_{1}}Механика (деформируемого) твёрдого тела (МДТТ или МТДТ) — естественная наука, часть механики сплошных сред, изучающая изменение формы твёрдых тел при внешних и внутренних воздействиях и движении. Следует отличать эту науку от физики твёрдого тела, которая изучает внутреннюю структуру твёрдых тел и новые материалы, и от кинематики абсолютно твёрдого тела.

Есть специальность «Механика деформируемого твёрдого тела» (шифр специальности — 01.02.04), признанная ВАК РФ в качестве раздела наук для защиты диссертаций.

Относительная позиция любых точек деформируемого твёрдого тела может изменяться. Такое тело обладает внутренними степенями свободы (в дополнение к поступательным и вращательным), которые обычно называют колебательными степенями свободы. Деформируемое тело без диссипационных степеней свободы называется абсолютно упругим телом; если же имеется диссипация, то тело называется неупругим.

Уравнения движения деформируемого тела намного более сложны чем для абсолютно твёрдого тела, так как необходима дополнительные координаты для учёта деформации тела. Теория малых смещений часто используется инженерами и физиками для решения проблем теории упругости, в которые вовлечена деформация. Это позволяет упростить проблему и облегчить её решение. Эти аппроксимации (приближения) позволяют методике очень сильно приблизиться к реальности, однако только до тех пор, пока деформации незначительные. Если необходимо описать большие смещения, часто используют метод конечных элементов. Деформации обычно характеризуются тензором деформации.

Тензор деформации характеризует сжатие (растяжение) и изменение формы в каждой точке тела при деформации:

{\displaystyle \varepsilon _{ij}={\frac {1}{2}}\left({\frac {\partial u_{i}}{\partial x_{j}}}+{\frac {\partial u_{j}}{\partial x_{i}}}+\sum \limits _{l}{\frac {\partial u_{l}}{\partial x_{i}}}{\frac {\partial u_{l}}{\partial x_{j}}}\right)}вектор, описывающий смещение точки тела: его координаты — разность между координатами близких точек после ({\displaystyle dx_{i}^{\prime }} ) и до ({\displaystyle dx_{i}} ) деформации. Дифференцирование производится по координатам в отсчётной конфигурации (до деформирования). Расстояния до и после деформации связаны через {\displaystyle \varepsilon _{ij}} :

{\displaystyle dl^{\prime 2}=dl^{2}+2\varepsilon _{ij}\,dx_{i}\,dx_{j}}>

(по повторяющимся индексам ведётся суммирование).

По определению тензор деформации симметричен, то есть {\displaystyle \varepsilon _{ij}=\varepsilon _{ji}} .

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение.

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение^[1].

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.

Момент импульса замкнутой системы сохраняется. Момент импульса является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения.

где {\displaystyle \mathbf {r} } — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, {\displaystyle \mathbf {p} } — импульс частицы.

Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:{\displaystyle \mathbf {L} =\sum _{i}\mathbf {r} _{i}\times \mathbf {p} _{i},}

где {\displaystyle \mathbf {r} _{i},\mathbf {p} _{i}} — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.

(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как {\displaystyle \mathbf {L} =\int \mathbf {r} \times \mathbf {dp} ,} где {\displaystyle \mathbf {dp} } — импульс бесконечно малого точечного элемента системы).

В системе СИ момент импульса измеряется в единицах джоуль-секунда.

Моментом инерции системы относительно оси вращения называется физическая величина, равная сумме произведения масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.

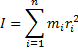
Момент инерции тела в случае непрерывного распределения массы равен

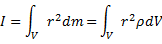
-интегрируется по всему объёму.

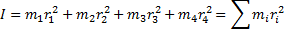
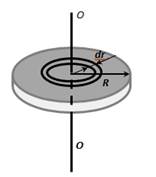1. Найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр. Разобьем диск на кольцевые слои толщиной dr. Все точки слоя будут находиться на одинаковом расстоянии от оси,равномr. Объем такого слоя равен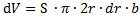

Площадь кольца

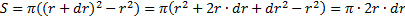
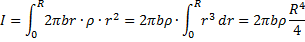
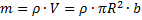
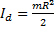
2. Полый тонкостенный цилиндр радиуса R (обруч, велосипедное колесо и тому 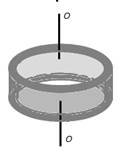подобное).

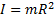
Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 10 расходы во входном и выходном сечениях напорной трубы равны:

q1 = q2.

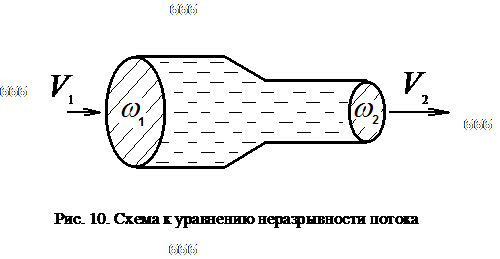
С учётом, что q = Vw, получим уравнение неразрывности потока:

V1 w1 = V2 w2 . (17)

Если отсюда выразим скорость для выходного сечения

V2 = V1 w1 /w2 , (18)

то легко заметить, что она увеличивается обратно пропорционально площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.

Рассмотрим пример.

Как изменится скорость потока, если диаметр напорной трубы d уменьшится в два раза? Площадь живого сечения такой трубы

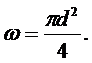(19)

Тогда отношение площадей в формуле (18) будет равно 4.

Таким образом, при уменьшении диаметра трубы в два раза — скорость потока увеличится в четыре раза. Аналогично, если диаметр уменьшится в три раза — скорость возрастёт в девять раз.

Опыты показывают, что возможны два режима (вида) движения жидкости в гидравлических линиях:

• ламинарный (от латинского слова lamina – слой),
• турбулентный (от латинского слова turbulentus – возмущенный, беспорядочный).

Ламинарным называют слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давлений. При ламинарном движении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, то есть поперечные перемещения жидкости отсутствуют. Такое движение является вполне упорядоченным и при постоянном давлении строго установившимся.

Турбулентным называют течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При таком движении векторы скоростей имеют не только осевые, но и нормальные к оси трубы составляющие, поэтому вместе с основным продольным движением жидкости вдоль трубы происходят поперечные перемещения (перемешивание) и вращение отдельных объемов жидкости. Этим объясняются пульсации скоростей и давлений.

Число Рейнольдса

Режим движения жидкости в трубе изменяется примерно при определенной средней по сечению скорости 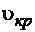, которую называют критической. Значение этой скорости прямо пропорционально кинематической вязкости и обратно пропорционально диаметру трубы:

.

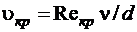Входящий в эту формулу безразмерный коэффициент пропорциональности 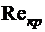(критическое число Рейнольдса) одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и кинематической вязкостью:

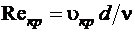. (1.5.1)

для труб круглого сечения .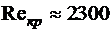

С физической точки зрения, критерий Рейнольдса 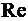есть отношение сил инерции потока к силам трения при движении жидкости.

При 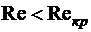движение жидкости является ламинарным, при 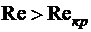- турбулентным.

В гидравлических приводах технологического оборудования устойчивое турбулентное течение жидкости в трубах наблюдается при .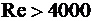

Упругие и квазиупругие силы

Рассмотрим тело массы m, закрепленное на пружине с коэффициентом жесткости k (массой пружины пренебрегаем). Растянем пружину на х. Тогда по закону Гука на тело будет действовать сила упругости F_упр :

1) величина силы пропорциональна величине отклонения системы от положения равновесия

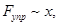
2) направление сила противоположно направлении смещения, т.е. сила всегда направлена к положению равновесия (при х > 0, F_упр < 0, при х < 0, F_упр > 0)

3) В положении равновесия х = 0 и F_упр = 0.

По закону Гука

F_упр = -kх.

Систему, состоящую из материальной точки массы m и абсолютно упругой пружины с коэффициентом жесткости k, в которой возможны свободные колебания, называют пружинным маятником.

Запишем второй закон Ньютона для рис. б

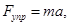
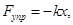
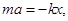
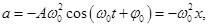
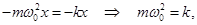
т.е.

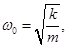
тогда

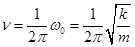
и

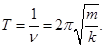
Если сила не является по своей природе упругой, но подчиняется закону F = -kх, то она называется квазиупругой силой.

Получим уравнение пружинного маятника. Учтем в записи второго закона Ньютона, что

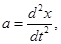
тогда

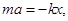
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Вынужденными колебаниями называются незатухающие колебания системы, которые вызываются действием внешней периодической силы.

Сила, вызывающая вынужденные колебания, называется вынуждающей или возмущающей силой.

Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.

Принцип Гюйгенса является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка фронта (поверхности, достигнутой волной) является вторичным (т.е. новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.

Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Густав Кирхгоф придал принципу Гюйгенса строгий математический вид, показав, что его можно считать приближенной формой теоремы, называемой интегральной теоремой Кирхгофа.

Фронтом волны точечного источника в однородном изотропном пространстве является сфера. Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от точечного источника, одинакова.

Дальнейшим обобщением и развитием принципа Гюйгенса является формулировка через интегралы по траекториям, служащая основой современной квантовой механики.

Абсолютный ноль

Абсолю́тный нуль температу́ры (реже^[1] — абсолютный ноль температуры) — минимальный предел температуры, которую может иметь физическое тело во Вселенной. Абсолютный нуль служит началом отсчёта абсолютной температурной шкалы, например, шкалы Кельвина. В 1954 году X Генеральная конференция по мерам и весам установила термодинамическую температурную шкалу с одной реперной точкой — тройной точкой воды, температура которой принята 273,16 К (точно), что соответствует 0,01 °C, так что по шкале Цельсия абсолютному нулю соответствует температура −273,15 °C^[2].

В рамках применимости термодинамики абсолютный нуль на практике недостижим. Его существование и положение на температурной шкале следует из экстраполяции наблюдаемых физических явлений, при этом такая экстраполяция показывает, что при абсолютном нуле энергия теплового движения молекул и атомов вещества должна быть равна нулю, то есть хаотическое движение частиц прекращается, и они образуют упорядоченную структуру, занимая чёткое положение в узлах кристаллической решётки (жидкий гелий составляет исключение). Однако, с точки зрения квантовой физики и при абсолютном нуле температуры существуют нулевые колебания, которые обусловлены квантовыми свойствами частиц и физического вакуума, их окружающего^[2].

В 1703 г. французский физик Гийом Амонтон (фр. Guillaume Amontons) представил воздушный термометр, в котором за нуль шкалы принималась температура, при которой воздух «теряет всю свою упругость». Рассчитанное им значение составило −239,5 °C.

В кинетической теории теплоты М. В. Ломоносова теплота объясняется «коловратным» движением. Прекращение движения означает предельную степень холода (по современной терминологии, абсолютный нуль).

В вышедшей в 1779 г. работе «Пирометрия» немецкий учёный Ламберт (нем. Johann Heinrich Lambert) уточнил полученное Амонтоном значение и получил −270 °C^[3].

Теплопроводность газов

Теплопрово́дность — способность материальных тел к переносу энергии (теплообмену) от более нагретых частей тела к менее нагретым частям тела, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости.

Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В системе СИ единицей измерения коэффициента теплопроводности является Вт/(м·K).

Исторически считалось, что передача тепловой энергии связана с перетеканием гипотетического теплорода от одного тела к другому. Однако с развитием молекулярно-кинетической теории явление теплопроводности получило своё объяснение на основе взаимодействия частиц вещества. Молекулы в более нагретых частях тела движутся быстрее и передают энергию посредством столкновений медленным частицам в более холодных частях тела.

Второе начало термодинамики

Второе начало термодинамики (второй закон термодинамики) устанавливает существование энтропии^[1] как функции состояния термодинамической системы и вводит понятие абсолютной термодинамической температуры^[2], то есть «второе начало представляет собой закон об энтропии»^[3] и её свойствах^[4]. В изолированной системе энтропия остаётся либо неизменной, либо возрастает (в неравновесных процессах^[3]), достигая максимума при достижении термодинамического равновесия (закон возрастания энтропии)^[5][6][2]. Встречающиеся в литературе различные формулировки второго начала термодинамики представляют собой собой частные выражения общего закона возрастания энтропии^[5][6].

Второе начало термодинамики позволяет построить рациональную температурную шкалу, не зависящую от произвола в выборе термометрического свойства и способа его измерения^[7].

Вместе первое и второе начала составляют основу феноменологической термодинамики, которую можно рассматривать как развитую систему следствий этих двух начал. При этом из всех допускаемых первым началом процессов в термодинамической системе второе начало позволяет выделить фактически возможные^[7] и установить направление протекания самопроизвольных процессов, а также критерии равновесия в термодинамической системах.

Второе начало термодинамики возникло как рабочая теория тепловых двигателей, которая устанавливает условия, при которых превращение тепла в работу достигает максимального эффекта. Анализ второго начала термодинамики показывает, что малая величина этого эффекта ─ коэффициента полезного действия (КПД) ─ обуславливается не техническим несовершенством тепловых двигателей, а особенностью теплоты как способа передачи энергии, которая накладывает ограничения на его величину. Впервые теоретические исследования работы тепловых двигателей были проведены французским инженером Сади Карно. Он пришёл к выводу, что КПД тепловых машин не зависит от термодинамического цикла и природы рабочего тела , а целиком определяется в зависимости от внешних источников ─ нагревателя и холодильника. ^[8]Работа Карно была написана до открытия принципа эквивалентности теплоты и работы и всеобщего признания закона сохранения энергии. Свои выводы Карно основывал на двух противоречивых основаниях: теплородной теории, которая была вскоре отброшена, и гидравлической аналогии. Несколько позднее Р. Клаузиус и В. Томсон- Кельвин согласовали теорему Карно с законом сохранения энергии и заложили основу того, что сейчас составляет содержание второго начала термодинамики.

Для обоснования теоремы Карно и дальнейшего построения второго начала необходимо было ввести новый постулат.

Типы кристалических решеток

Твердые вещества, как правило, имеют кристаллическое строение. Оно характеризуется правильным расположением частиц в строго определенных точках пространства. При мысленном соединении этих точек пересекающимися прямыми линиями образуется пространственный каркас, который называют кристаллической решеткой.

Точки, в которых размещены частицы, называются узлами кристаллической решетки. В узлах воображаемой решетки могут находиться ионы, атомы или молекулы. Они совершают колебательные движения. С повышением температуры амплитуда колебаний возрастает, что проявляется в тепловом расширении тел.

В зависимости от вида частиц и характера связи между ними различают четыре типа кристаллических решеток: ионные, атомные, молекулярные и металлические.

Кристаллические решетки, состоящие из ионов, называются ионными. Их образуют вещества с ионной связью. Примером может служит кристалл хлорида натрия, в котором, как уже отмечалось, каждый ион натрия окружен шестью хлорид-ионами, а каждый хлорид-ион — шестью ионами натрия. Такому расположению соответствует наиболее плотная упаковка, если ионы представить в виде шаров, размещенных в кристалле . Очень часто кристаллические решетки изображают, как показано на рис 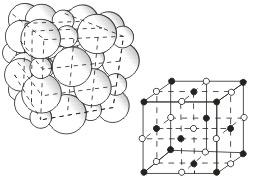, где указывается только взаимное расположение частиц, но не их размеры.

Число ближайших соседних частиц, вплотную примыкающих к данной частице в кристалле или в отдельной молекуле, называется координационным числом.

В решетке хлорида натрия координационные числа обоих ионов равны 6. Итак, в кристалле хлорида натрия нельзя выделить отдельные молекулы соли. Их нет. Весь кристалл следует рассматривать как гигантскую макромолекулу, состоящую из равного числа ионов Na⁺ и Cl^—, Na_nCl_n, где n — большое число . Связи между ионами в таком кристалле весьма прочны. Поэтому вещества с ионной решеткой обладают сравнительно высокой твердостью. Они тугоплавки и малолетучи.

Плавление ионных кристаллов приводит к нарушению геометрически правильной ориентации ионов относительно друг друга и уменьшению прочности связи между ними. Поэтому расплавы их проводят электрический ток. Ионные соединения, как правило, легко растворяются в жидкостях, состоящих из полярных молекул, например в воде.

Кристаллические решетки, в узлах которых находятся отдельные атомы, называются атомными. Атомы в таких решетках соединены между собой прочными ковалентными связями. Примером может служить алмаз — одна из модификаций углерода. Алмаз состоит из атомов углерода, каждый из которых связан с четырьмя соседними атомами. Координационное число углерода в алмазе 4 . В решетке алмаза, как и в решетке хлорида натрия, молекулы отсутствуют. Весь кристалл следует рассматривать как гигантскую молекулу. Атомная кристаллическая решетка характерна для твердого бора, кремния, германия и соединений некоторых элементов с углеродом и кремнием.

Кинематика вращательного движения

• Часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение, называется механикой. Классическая механика (механика Ньютона-Галилея) изучает законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме.
• Кинематика – раздел механики, предметом изучения которого является движение тел без рассмотрения причин, которыми это движение обусловлено.
• В механике для описания движения тел в зависимости от условий конкретных задач используются различные физические модели: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело.
• Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение. Совокупность тела отсчета, связанной с ним системы координат и синхронизированных между собой часов называется системой отсчета.
• Вектор Δr=r-r₀, проведенный из начального положения движущейся точки в положение ее в данный момент времени называется вектором перемещения. Линия, описываемая движущейся материальной точкой (телом) относительно выбранной системы отсчета называется траекторией движения. В зависимости от формы траектории различают прямолинейное и криволинейное движение. Длина участка траектории, пройденного материальной точкой за данный промежуток времени, называется длиной пути.
• Скорость – это векторная физическая величина, которая характеризует быстроту движения и его направление в данный момент времени. Мгновенная скорость определяется первой производной радиуса-вектора движущейся точки по времени:

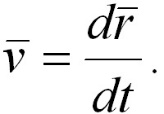
Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Модуль мгновенной скорости материальной точки равен первой производной длины ее пути по времени:

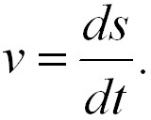
• Ускорение – векторная физическая величина для характеристики неравномерного движения. Она определяет быстроту изменения скорости по модулю и направлению. Мгновенное ускорение - векторная величина, равная первой производной скорости по времени:

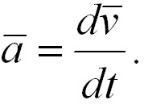
Динамика вращения

Описанное нами движение твердого тела относительно неподвижной точки является основным видом движения. Однако вычислить вектор – момент импульса системы относительно произвольной точки – не просто: надо знать шесть проекций (три задают положение тела, три задают положение точки).
Значительно проще найти момент импульса тела, вращающегося вокруг неподвижной оси z (рис. 6.4). В этом случае составляющие – момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления. Вращение вокруг оси z происходит только под действием M_z .

Пусть некоторое тело вращается вокруг оси z (рис. 6.5).

Рис. 6.4	Рис. 6.5

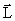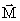Получим уравнение динамики для некоторой точки m_i этого тела, находящегося на расстоянии R_i от оси вращения. При этом помним, что и направлены всегда вдоль оси вращения z, поэтому

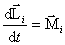или .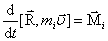

Поскольку 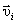у всех точек разная, введем вектор угловой скорости 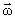, причем 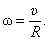. Тогда .
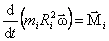Так как тело абсолютно твердое, то в процессе вращения m_i и R_i останутся неизменными. Тогда

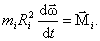
Обозначим I_i – момент инерции точки находящейся на расстоянии R от оси вращения:

.

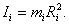(6.2.1)

Момент инерции тела служит мерой инертности во вращательном движении.
В общем случае тело состоит из огромного количества точек, и все они находятся на разных расстояниях о