ТЕМА: Элементы теории неравновесных процессов

Задачи

Задача 1. Рассмотреть применение принципа Ле Шателье для случая стационарного состояния при термодиффузии.

Решение. Представим себе, что в смеси поддерживается температурный градиент, вызывающий появление градиента концентрации. Предположим также, что смесь состоит из двух компонентов. Пусть концентрация компоненты 1 увеличивается у горячей стенки резервуара, в котором эта смесь заключена. Добавим некоторое количество вещества в холодную часть резервуара. Тогда градиент концентрации понижается. По принципу Ле Шателье, возникает поток, который перемещает некоторое количество вещества 1 к горячей стороне резервуара. Таким образом, возмущение компенсируется этим потоком, как этого требует принцип Ле Шателье.

Задача 2. Найти дифференциальную формулу динамического уравнения состояния однородной системы и, пользуясь им, определить выражение для релаксации объема, температуры и давления.

Решение. Рассмотрим закрытую систему, в которой протекает процесс релаксации соответствующий внутреннему параметр у 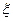. Пусть система немного отклоняется от исходной системы, которая характеризуется температурой 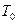, давлением 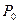и внутренним параметром 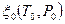. Подобно формуле

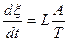. (1)

при условиях близких к равновесию,

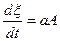, (2)

где A – сродство внутреннего превращения,

a – феноменологический коэффициент, зависящий от , , .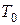

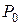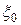Выбираем в качестве независимых параметров 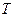и 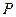. Тогда 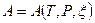. Как и в случае (1), в исходном состоянии 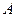равно нулю. Для условий близких к начальным имеем

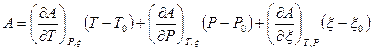. (3)

Уравнение состояния системы вблизи исходного состояния можно представить в виде

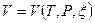. (4)

Входящие в формулы (3) и (4) частные производные относятся к исходному состоянию и, следовательно, для данной системы постоянны. Выразим их через термодинамические коэффициенты:

,

,

,

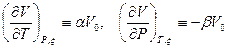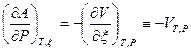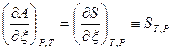где 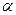- коэффициент расширения;

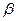- коэффициент изотермической сжимаемости;

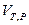- изменение объема в результате реакции;

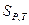- энтропия реакции.

Уравнения (2) и (4) принимают такой вид:

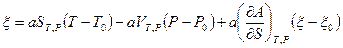, (6)

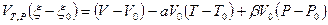. (7)

Дифференцируя уравнение (7) по времени получаем

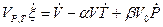. (8)

Исключая 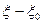и 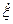из уравнений (6) - (8), находим

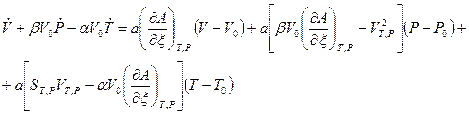(9)

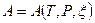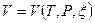Так как и , то

,

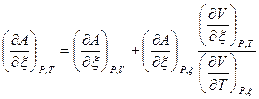а используя формулу (5) получаем

.

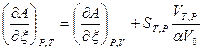Аналогично

.

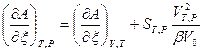Поэтому уравнение (9) принимает вид

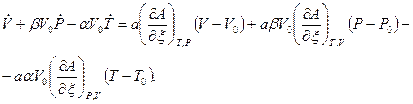(10)

Введем времена релаксации изотермоизобарного 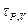, изотермоизохорного 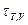и изобарноизохорного 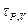процессов внутреннего превращения:

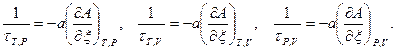
Используя эти соотношения в формуле (10) получаем динамическое уравнение состояния в дифференциальной форме:

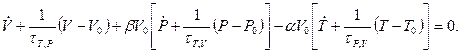
Оно связывает переменные 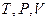и их производные 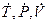. В него входят величины, определяемые из условий равновесия ( 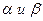) и три времени релаксации 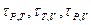. Если все эти величины известны, то можно, например, определить изменение объема со временем, т.е. получить 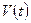, если давление и температура заданны как функции времен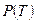и: и .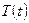

Для объемной релаксации при постоянной температуре и постоянном давлении получаем

;

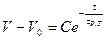для релаксации давления при постоянной температуре и объеме получаем

;

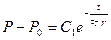для температурной релаксации при постоянном объеме и давлении получаем

,

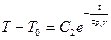где 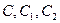- постоянные интегрирования, зависящие от начальных условий.

Задача 3. Выразить коэффициенты Пельтье, Томсона и термоэлектродвижущей силы через поток энтропии, вызванный движением заряженных частиц.

Решение.Если подставитьв выражение для плотности потока энтропии в термически неоднородном проводнике с током выражение 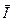из формулы 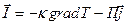, то

.

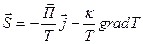Здесь первое слагаемое определяет поток энтропии, вызванный движением зарядов, а второе теплопроводностью. Обозначим величину первого слагаемого через 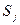. Тогда 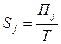и 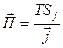. Пользуясь вторым соотношением Томсона 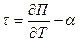, получаем

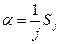и .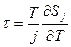

Аналогично,

.

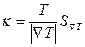Отсюда видно, что термоэлектрические явления связаны с переносом энтропии, чем объясняется их известная “обратимость”.

Задача 4. Применима ли термодинамика необратимых процессов к живым организмам?

Решение. Термодинамика изучает общие закономерности систем из большого числа частиц в независимости от специфических особенностей рассматриваемых объектов и механизмов протекания в них процессов. Это позволяет распространять положения термодинамики на любые системы, в том числе живые организмы, если в системах выполняются ограничения, выдвигаемые термодинамикой.

Классическая термодинамика рассматривающая равновесные процессы, весьма приближенно применима к биологии, поскольку живые организмы не находятся в состоянии равновесия. Этим объясняется то, что многочисленные попытки использования равновесной термодинамики для анализа жизненных явлений оказались неудачными.

Живой организм при термодинамическом рассмотрении представляет собой открытую систему, внутри которой протекают различные необратимые процессы (химические реакции, диффузия, осмос и т.д.). Поэтому к биологическим системам гораздо лучше применимы положения термодинамики необратимых процессов.

Определенным количественным ограничением применимости изложенной термодинамики необратимых процессов к описанию жизнедеятельности организмов является ее линейность, соответствующая рассмотрению систем, не слишком далеко отстоящих от положения равновесия и процессы, протекающие в них, являются существенно необратимыми.

Линейная термодинамика не в силах объяснить процессы роста и дифференцировки клеток, возникновение новых структур. Расширение термодинамики на сильно неравновесные системы, в которых связь между термодинамическими потоками и силами перестает быть линейной, осуществлено в последнее десятилетие Пригожиным и Глансдорфом и привело к построению нелинейной неравновесной термодинамики. Основу этой термодинамики составляет критерий эволюции Пригожина – Глансдорфа, согласно которому в сильно неравновесной системе скорость производства энтропии уменьшается.

Занятие №4

ТЕМА: Производство энтропии

Задачи

Задача 1. На примере процесса теплопроводности в системе показать, что допущение локального равновесия позволяет вычислить при переходе от отдельных элементов объема к системе в целом изменение энтропии, вызванное необратимостью этого процесса.

Решение. Выделим в неравномерно нагретом теле некоторый объем. При допущении локального равновесия и отсутствии потока частиц основное уравнение термодинамики необратимых процессов для рассматриваемого объема принимает вид

.

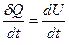Если 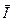- плотность потока теплоты, то энергия в данном объеме может изменятся только за счет притока теплоты извне через поверхность 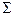, ограничивающую выделенный объем, поэтому

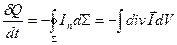
и количество теплоты, сообщенное элементу объема,

,

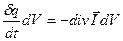откуда,

,

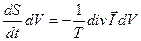и изменение энтропии системы

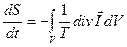
или

,

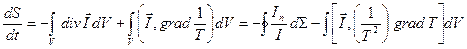где 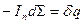- количество теплоты, которое входит в систему через элемент поверхности. Учитывая, что 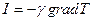, получаем

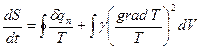. (1)

Здесь первое слагаемое определяет изменение энтропии системы, за счет притекающей в нее теплоты. Эта величина и стоит в правой части неравенства Клаузиуса классической термодинамики. Второе слагаемое представляет собой изменение энтропии, вызванное необратимостью процесса теплопроводности внутри выделенного объема. Так как этот член внутри положителен, то выражение (1) не противоречит неравенству Клаузиуса.

Задача 2. Найти производство энтропии при процессе перехода теплоты от одного тела к другому.

Решение. Когда при тепловом контакте двух тел, однако, с температурой 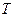получает количество теплоты 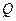, а другое тело с температурой 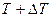отдает эту теплоту, то суммарное изменение энтропии (при малом )

.

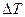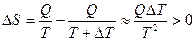Если за интервал времени 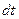произошел обмен теплотой в объеме 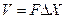( 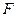- площадь соприкосновения тел) , то скорость возникновения энтропии в единице объема

,

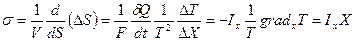где 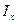- составляющая по оси 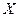плотность потока теплоты;

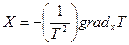- соответствующая этому потоку сила.

.

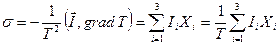Задача 3. Определить производство энтропии в электрической цепи.

Решение. Если в цепи с Э.Д.С. 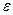протекает ток силой 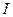, то по закону Джоуля-Ленца в ней выделяется в единицу времени количество теплоты 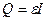, а в единице объема контура (в общем случае и не однородного) в единицу времени выделяется теплота

,

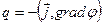где 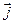- плотность тока; 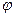- потенциал электрического поля. В стационарном состоянии, когда температура контура поддерживается постоянной, электрическая энергия полностью передается в виде теплоты окружающей среде. Поэтому скорость возникновения энтропии в контуре

,

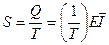а производство энтропии, т.е. скорость ее локального возникновения

.

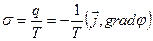Задача 4. Показать, что кинетические коэффициенты 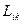обладают следующими свойствами:

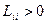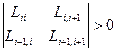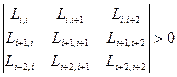, , и т.д.

Решение. Производство энтропии представляет собой положительно определенную квадратичную форму термодинамических сил

.

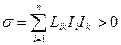Но квадратичная форма является положительно определенной, если детерминант, составленный из ее коэффициентов 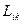и его диагональные миноры, получившиеся последовательным вычеркиванием строк и столбцов, положительны. Эти условия на коэффициенты 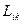и выражают указанные в условии задачи их свойства.

Задача 5. Вычислить среднюю энтропию, 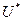переносимую молем газа Кнудсена при прохождении через малое отверстие, соединяющие два резервуара с газом.

Решение. Найдем среднюю энтропию 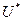, переносимой молекулой при прохождении через отверстие в случае ультразаряженного газа Кнудсена, когда диаметр отверстия, соединяющего два резервуара с газом, мал по сравнению со средней длинной свободного пробега молекулы.

Пусть ось 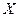перпендикулярна плоскости отверстия. Если 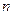- плотность числа молекул, то средняя плотность молекул, имеющих составляющую по оси 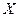, скорость в пределах от 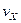до 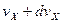, по Максвеллу равна

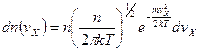
Средний поток молекул через единицу площади отверстия в единицу времени

.

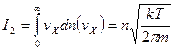Средний поток энергии в единицу времени через единицу площади отверстия по оси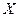

.

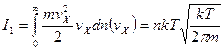Каждая молекула переносит кинетическую энергию

.

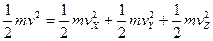Среднее значение 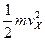для тех молекул, которые проходят через отверстие, равно отношению среднего потока энергии к среднему потоку молекул:

.

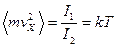Эта величина в 2 раза больше средней кинетической энергии на одну степень свободы 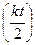, поскольку молекулы с большими скоростями имеют большую вероятность пройти через отверстие, чем молекулы с меньшими скоростями.

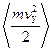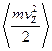Средние значения и равны 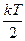. Поэтому средняя энергия, переносимая проходящими через отверстие молекулами,

,

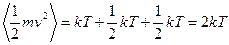а средняя молярная энергия переноса

.

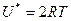Задача 5. Показать, что при установлении стационарного состояния в двух соединенных капилляром сосудах с газом Кнудсена энтропия газов уменьшается.

Решение. Согласно принципу Пригожина, по мере перехода системы в стационарное состояние производство энтропии уменьшается и, когда стационарное состояние достигнуто, эта величина принимает наименьшее значение, совместимое с внешними условиями. Сама энтропия системы в этом процессе установления стационарного состояния также часто уменьшается. Покажем это на примере с газом Кнудсена. Пусть соединенные капилляром сосуды с газом Кнудсена имеют одинаковый объем и в начальном состоянии имеют по молю газа:

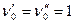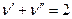, . (1)

Распределение вещества в стационарном состоянии определяется уравнением

,

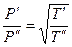или

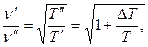
(2)

Поскольку 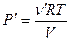и 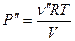из второго уравнения (1) и уравнения (2) находим:

, .

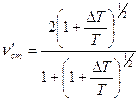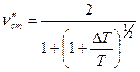Энтропия 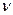молей идеального газа

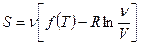и .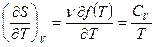

Поэтому энтропия системы

.

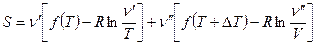применяя это уравнение к начальному и стационарному состояниям, и разлагая потом 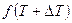по степеням 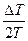, получаем

.

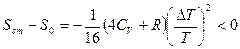Это означает, что энтропия системы в стационарном состоянии меньше, чем в начальном. То же самое наблюдается при термодиффузии. Происходящее при этом разделение веществ соответствует уменьшению энтропии по сравнению с начальным состоянием. Однако в некоторых других случаях энтропия возрастает.

Занятие №5

ТЕМА: Кинетика

Задачи

Задача 1. Водород находится в сосуде при температуре 300 К и давлении 2 атм.. Принимая во внимание распределение Больцмана по скоростям, вывести формулу для давления газа и вычислить число столкновений в 1 с, испытываемых участком стенки сосуда площадью 10 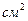. Чему равно среднее время между двумя столкновениями?

Решение. Будем предполагать, что между не имеющими размеров молекулами идеально газа не происходит столкновений. В то же время учтем распределение скоростей по абсолютной величине и по направлениям. Рассмотрим на стенке сосуда площадку размером 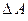и определим число попадающих на эту площадку за время dt частиц, имеющих скорость от v до v + dv,

и угол падения от 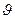до 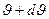. Эти частицы заключены в цилиндре, объем которого равен

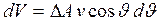(1)

(рис.2). Из числа содержащихся в 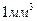частиц под углом к стенке, лежащем в пределах от 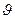до 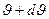, движутся

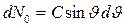(2)

частиц, имеющих произвольный азимутальный угол 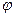. (Фактически при фиксированном угле 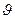молекулы летят из пространства между двумя конусами.- Ред.). Величину С определим из условия

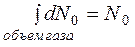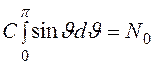или (3)

откуда

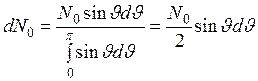. (4)

Если теперь учесть распределение скоростей Максвелла – Больцмана, то для числа dv частиц, сталкивающихся с площадкой 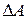и имеющих при этом скорость и угол падения, заключенных в интервалах от v до v + dv, и от 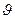до 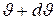, согласно (1) и (4) получаем

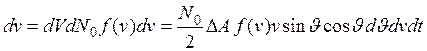, (5)

где f(v) – функция распределения.

При каждом соударении стенке передается импульс

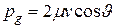. (6)

Отсюда находим силу, действующую на площадку :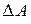

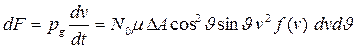. (7)

Полную силу, приложенную к площадке 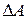, получим посредством интегрирования по всем углам падения 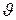и по всем скоростям v. В результате после деления на 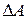находим давление

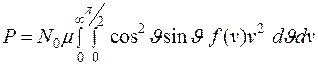(8)

Интегрирование по углу 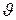в (8) дает

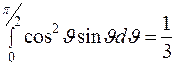, (9)

а интегрируя по скоростям, получаем

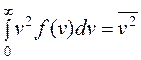. (10)

Таким образом, статистическая модель, учитывающая больцмановское распределение по скоростям, приводит к следующему выражению для давления:

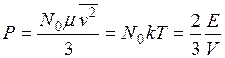. (11)

Подставляя сюда вместо числа частиц в 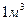выражение 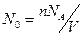и используя соотношение 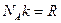, получаем

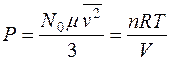. (12)

Для вычисления среднего числа столкновений необходимо проинтегрировать выражение (5). Тогда для числа столкновений, происходящих за 1 с, имеем

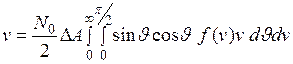. (13)

Необходимые нам интегралы имеют следующие значения:

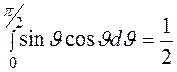, (14)

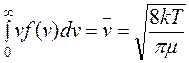. (15)

Таким образом, для числа столкновений в единицу времени имеем

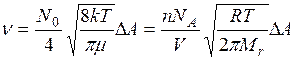, (16)

где 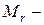относительная молекулярная масса, 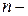число кило-молей в объеме V. Используя уравнение состояния идеального газа, можно записать выражение (16) для числа столкновений в в виде

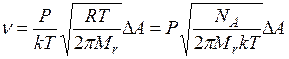. (17)

Подставляя численные значения, найдем число столкновений с участком площадью :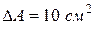

.

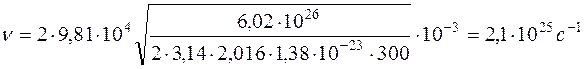Отсюда определяем среднее время между двумя столкновениями с площадкой :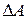

.

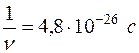Задача 2. Вычислить число столкновений молекул водорода при температуре 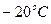и давления 0,5 атм. Чему равна средняя длина свободного пробега 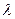? Найти полное число столкновений в 1 кмоле водорода. Молекулы рассматривать как невзаимодействующие твердые шары, движущиеся с одинаковыми скоростями. Газокинетический эффективный диаметр принять равным .

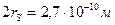Решение. Рассмотрим две частицы, которые движутся со скоростям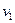и и 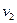. Если 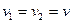, то их относительная скорость составляет

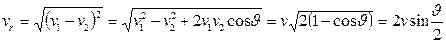, (1)

где 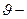угол между векторами этих скоростей. Усреднение по всем направлениям дает

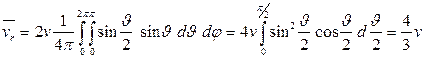. (2)

С данной молекулой за 1 с в среднем столкнуться все молекулы, центры тяжести которых окажутся внутри кругового цилиндра с основанием 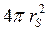и высотой 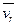. Если в 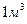содержится 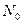, то число столкновений для одной частицы составляет

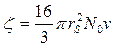. (3)

В качестве величины v используем среднее значение для распределения Максвелла – Больцмана

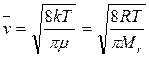. (4)

Величину 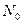найдем из уравнения состояни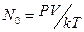я для 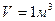. Тогда формула (3) дает для числа столкновений

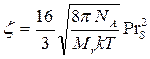. (5)

В рассматриваемой модели средняя длина свободного пробега есть

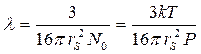. (6)

В 1 кмоль содержится 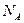молекул. Полное число столкновений, происходящих в 1 кмоле за 1 с, составляет

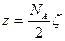. (7)

Подставив численные выражения, получим ,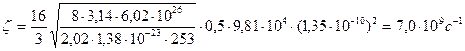

.

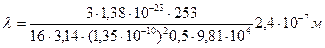
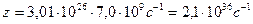Задача 3. Смесь из 3 л водорода и 1 л азота находится при нормальных условиях. Найти число столкновений между молекулами в 1 с. Чему равны средние длины пробега между соударениями различных частиц?(Диаметр газокинетического эффективного сечения составляет: ,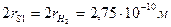

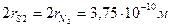, относительные молекулярные массы: , .).

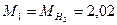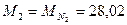Решение. Число столкновений частиц сорта 1 с частицами сорта 2 составляет

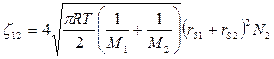. (1)

Аналогично получим число столкновений частиц 2 с частицами 1

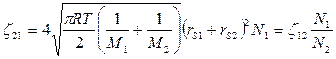. (2)

Полное число соударений частиц 1 и 2 в объеме 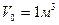, есть

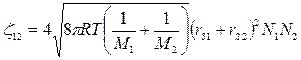. (3)

В данном случае полный объем газа 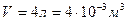. Для парциальных давлений имеем 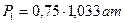, , 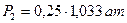а плотность числа частиц , ( ).

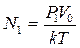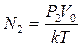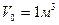Число столкновений между частицами двух в объеме V = 4л равно

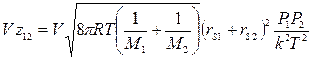; (4)

При заданных числовых значениях имеем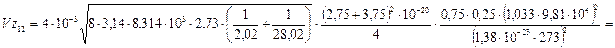

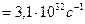
Средняя длина свободного пробега частицы 1 между соударениями с частицами 2 составляет

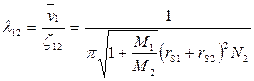. (5)

Подставив численные значения, получим длину свободного пробега молекул водорода между столкновениями с молекулами азота:

.

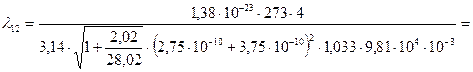
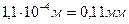Для средней длины свободного пробега молекул азота между столкновениями с молекулами водорода имеем

.

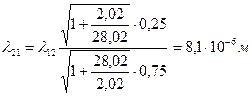Задача 4. В тонкостенном сосуде, помещенном в вакуум, имеется очень маленькое отверстие, на которое извне направляется параллельный пучок одноатомных молекул, летящих с одной и той же скоростью 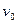, перпендикулярно к площади отверстия. Концентрация молекул в пучке равна 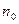. Найти в установившемся равновесном состоянии среднюю скорость 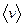, концентрацию молекул 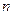и температуру 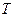газа в сосуде.

Решение. Из-за столкновений молекул со стенками сосуда и между собой внутри сосуда устанавливается максвелловское распределение скоростей. Условие сохранения числа частиц и кинетической энергии газа в сосуде имеют вид

, .

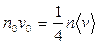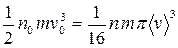Используя их, а также формулу 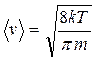, находим

, , .

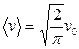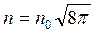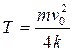Задача 5. Найти полную кинетическую энергию 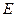молекул идеального одноатомного газа, ударяющихся о квадратный сантиметр стенки в единицу времени.

Ответ: 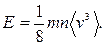Для максвелловского распределения .

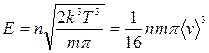Задача 6. В тонкостенном сосуде, содержащем идеальный одноатомный газ при температуре 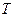, имеется очень маленькое отверстие, через которое молекулы вылетают в вакуум. Определить среднее значение 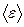кинетической энергии вылетевшей молекулы в предположении, что за время опыта изменения числа молекул и температуры газа в сосуде пренебрежимо малы.

Ответ: .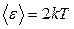

Задача 7. Определить, какая часть молекул идеального газа, столкнувшихся со стенкой сосуда за определенное время (например, за одну секунду), имеет кинетическую энергию, превосходящую .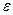

Ответ: .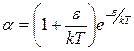

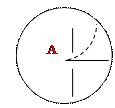
Задача 8. В опыте Штерна на поверхности вращающегося цилиндра С конденсируются молекулы серебра с различными скоростями. Каким скоростям молекул, попадающих на пластинку DF, соответствует ее наибольшее почернение?

Решение.

F

	C

D

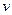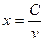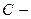Если установка неподвижна, то молекулы конденсируются в точке D. При вращении всей установки молекулы со скоростями попадают в F. Смещение по дуге DF равно , где постоянная прибора. Число молекул 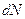со скоростями между 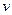и 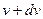, ежесекундно испускаемых источником A, пропорционально 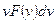. Выражая 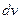через 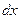, подставим его в виде 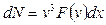. Отсюда видно, что линейная плотность распределения молекул, сконденсировавшихся по поверхности цилиндра, пропорциональна 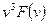, т.е. 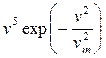. Эта плотность максимальна при 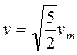, где 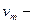наиболее вероятная скорость.

Задача 9. Газ состоит из молекул с массам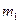и и 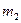, концентрации которых равны соответственно 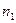и 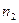. Найти выражение для средней длины свободного пробега молекулы каждого газа с учетом максвелловского распределения скоростей.

Ответ: ,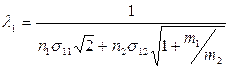

.

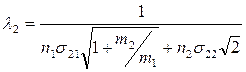Задача 10. Для приближенного вычисления средней длинны свободного пробега молекулы, Клаузиус предположил, что все молекулы газа движутся с одинаковыми скоростями, направления которых распределены в пространстве изотропно. Получить выражение для 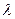в этом предположении.

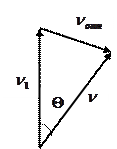Решение.

Найдем среднюю скорость молекул относительно одной из них (например, правой). Относительная скорость молекулы, движущейся под углом 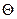к скорости первой молекулы 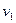, определяется выражением

.

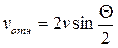Число молекул, скорости которых образуют с направлением 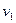углы между 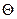и 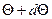, дается формулой

.

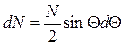Используя ее, получаем

.

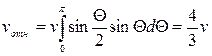После этого по формуле

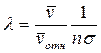
находим

.

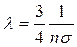Задача 11. Найти выражение для среднего полного числа столкновений 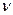молекул газа в единице объема газа в единицу времени.

Решение. Число столкновений одной молекулы с остальными дается выражением

.

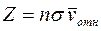Для 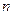молекул его надо умножить на 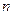и разделить на два. Деление на два необходимо потому, что при нашем подсчете каждая молекула учитывается дважды: один раз как ударяющая, другой – как ударяемая. В результате получаем

.

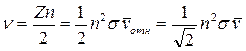Задача 12. Газ состоит из смеси двух газов с концентрациям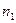и и 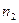. Найти выражение для среднего полного числа столкновений 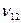молекул одного газа с молекулами другого газа в единице объема в единицу времени.

Ответ: .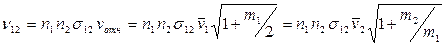

Задача 13. Показать, что в системе центра масс рассеяние шаров при упругих столкновениях сферически симметрично.

Решение. Пусть скорость 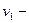скорость первого, а 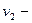скорость второго шара ( см.рис.). В системе центра масс

.

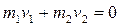При столкновении шары в этой системе обмениваются нормальными компонентами импульсов, тогда, как касательные компоненты их остаются неизменными. Отсюда следует, что скорости шаров в системе центра масс не изменяются по величине, а только поворачиваются на один и тот же угол