Интегралы от тригонометрических функций, умноженных на многочлен

Общее правило: за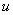 всегда обозначается многочлен

Пример 7

Найти неопределенный интеграл.

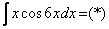
Интегрируем по частям:

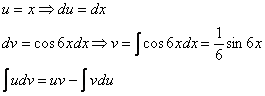
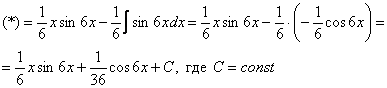
Хммм, …и комментировать нечего.

Пример 8

Найти неопределенный интеграл

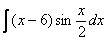
Это пример для самостоятельного решения

Пример 9

Найти неопределенный интеграл

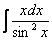
Еще один пример с дробью. Как и в двух предыдущих примерах за 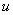обозначается многочлен.

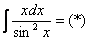
Интегрируем по частям:

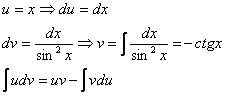
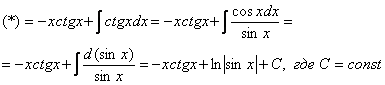
Если возникли трудности или недопонимание с нахождением интеграла , то рекомендую посетить урок Интегралы от тригонометрических функций.

Пример 10

Найти неопределенный интеграл

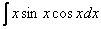
Это пример для самостоятельного решения.

Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.

Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….

Интегралы от обратных тригонометрических функций.
Интегралы от обратных тригонометрических функций, умноженных на многочлен

Общее правило: за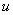 всегда обозначается обратная тригонометрическая функция.

Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»

Пример 11

Найти неопределенный интеграл.

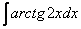
Решаем.

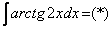
Интегрируем по частям:

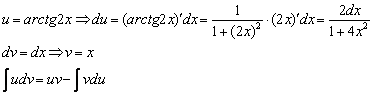
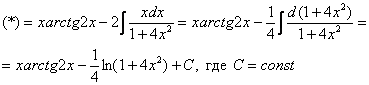
Интеграл 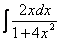найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример мы разбирали на уроке Метод замены переменной в неопределенном интеграле.

Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.

Пример 12

Найти неопределенный интеграл.

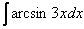
Это пример для самостоятельного решения

И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.

Пример 13

Найти неопределенный интеграл.

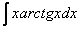
Что касаемо интегрирования по частям, почти всё разобрали. Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.

А сейчас, как любила говорить моя учительница по математике, пора кончать.

Желаю успехов!

Пример 3:Решение:

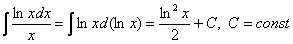
Пример 4:Решение:

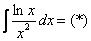
Интегрируем по частям:

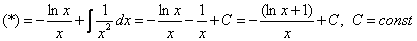
Пример 6:Решение:

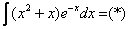
Дважды интегрируем по частям:

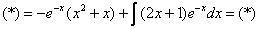
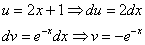
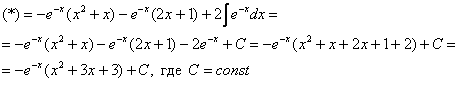
Пример 8:Решение:

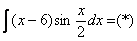
Интегрируем по частям:

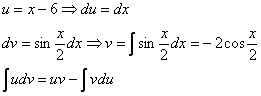
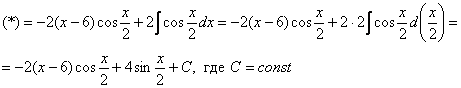
Пример 10:Решение:

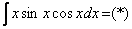
Интегрируем по частям:

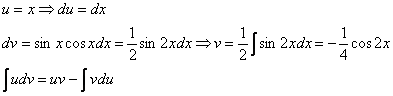
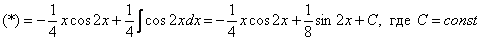
Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла 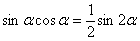. Её можно было использовать и сразу: 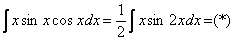, а потом интегрировать по частям.

Похожим способом также решаются интегралы вроде 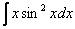, 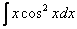– в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.

Пример 12: Решение:

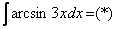
Интегрируем по частям:

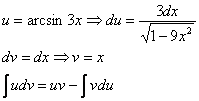
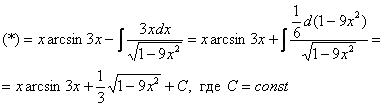
Пример 13: Решение:

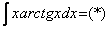
Интегрируем по частям:

Определенный интеграл. Примеры решений

И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.

Для того чтобы научиться решать определенные интегралы необходимо:

1) Уметь находить неопределенные интегралы.

2) Уметь вычислить определенный интеграл.

Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.

В общем виде определенный интеграл записывается так:

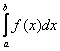
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой .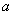
Верхний предел интегрирования стандартно обозначается буквой .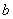
Отрезок 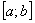называется отрезком интегрирования.

Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.

Что такое определенный интеграл? Считаю немного преждевременным рассказать про разбиения отрезка и предел интегральных сумм, поэтому пока я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.

Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:

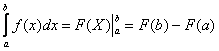
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию 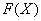(неопределенный интеграл). Обратите внимание, что константа 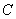в определенном интеграле не добавляется. Обозначение 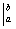является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись 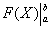? Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию: .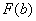

3) Подставляем значение нижнего предела в первообразную функцию: .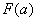

4) Рассчитываем (без ошибок!) разность 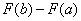, то есть, находим число.

Готово.

Всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла 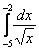не существует, поскольку отрезок интегрирования 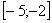не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: 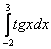. Такого интеграла тоже не существует, так как в точках 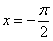, 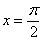отрезка 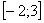не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.

Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция быланепрерывнойна отрезке интегрирования.

Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывнана отрезке интегрирования. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:

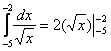???! Нельзя подставлять отрицательные числа под корень! Что за фигня?! Изначальная невнимательность.

Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде 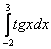, то нужно дать ответ, что интеграла не существует и обосновать – почему.

Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике.

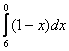– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.

В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:

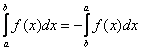
Например, в определенном интеграле перед интегрированием 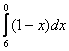целесообразно поменять пределы интегрирования на «привычный» порядок:

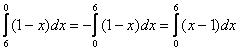– в таком виде интегрировать значительно удобнее.

Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:

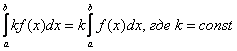
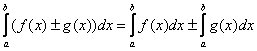– это справедливо не только для двух, но и для любого количества функций.

В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.

Для определенного интеграла справедлива формула интегрирования по частям:

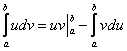
Пример 1

Вычислить определенный интеграл

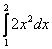
Решение:

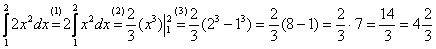
(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы 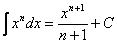. Появившуюся константу 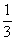целесообразно отделить от 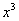и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

(3) Используем формулу Ньютона-Лейбница 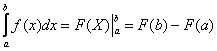. Сначала подставляем в 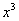верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Пример 2

Вычислить определенный интеграл

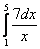
Это пример для самостоятельно решения, решение и ответ в конце урока.

Немного усложняем задачу:

Пример 3

Вычислить определенный интеграл

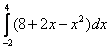
Решение:

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

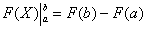
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: 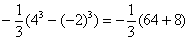– первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут 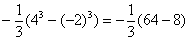(особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.

Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:

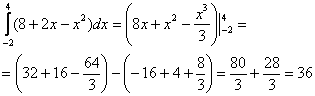
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов: 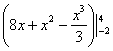(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.

Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.

Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная 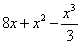находится в одной скобке.