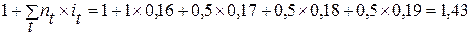Практика расчета процентов для краткосрочных ссуд

Поскольку процентная ставка, как правило, устанавливается в расчете за год, то при сроке ссуды менее года необходимо определить, какая часть годового процента выплачивается кредитору. Аналогичная проблема возникает и в случаях, когда срок ссуды меньше периода начисления.

Рассмотрим наиболее распространенный в практике случай – с годовыми периодами начисления. Очевидно, что срок ссуды необязательно равен целому числу лет. Выразим срок n в виде дроби

,

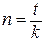где t – число дней ссуды;

k – число дней в году (временная база начисления процентов).

При расчете процентов применяют две временные базы:

1) k = 360 дней (12 месяцев по 30 дней). Это обыкновенные или коммерческие проценты;

2)k = 365, 366 дней. При использовании действительной продолжительности года (365, 366 дней) рассчитывают точные проценты.

Число дней ссуды также можно измерить приближенно и точно.

В первом случае продолжительность ссуды определяется из условия, согласно которому любой месяц принимается равным 30 дням.

Точное число дней ссуды определяется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения. День выдачи и день погашения считаются за один день.

Итак, возможны и применяются на практике три варианта расчета простых процентов.

1. Точные проценты с точным числом дней ссуды. Этот вариант, естественно дает самые точные результаты. Данный способ применяется центральными банками многих стран и крупными коммерческими банками, например, в Великобритании, США. В коммерческих документах он обозначается как 365/365 или АСТ/АСТ.

2. Обыкновенные проценты с точным числом дней ссуды. Этот метод, иногда называемый банковским, распространен в межстрановых ссудных операциях коммерческих банков, во внутристрановых – во Франции, Бельгии, Швейцарии. Он обозначается, как 365/360 или АСТ/360.

3. Обыкновенные проценты с приближенным числом дней ссуды. Такой метод применяется тогда, когда не требуется большой точности, например, при промежуточных расчетах. Он принят на практике коммерческих банков Германии, Швеции, Дании. Метод условно 360/360.

Пример: Ссуда 1 млн. руб. выдана 20.01. по 05.10. включительно. Какую сумму должен выплатить должник в конце срока, используя простую процентную ставку 18% годовых, по трем вариантам начисления простых процентов по краткосрочным ссудам? Год невисокосный.

Точное число дней – 258, приближенное – 255.

Точные проценты с точным числом дней ссуды:

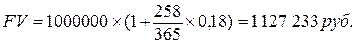
Обыкновенные проценты с точным числом дней ссуды:

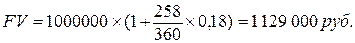
Обыкновенные проценты с приближенным числом дней ссуды:

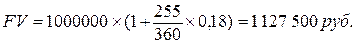
В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки. Если это простые ставки, то наращенная на конец срока сумма определяется следующим образом:

,

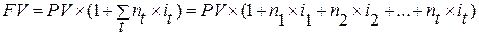где i_t – ставка простых процентов в периоде t;

n_t – продолжительность периода с постоянной ставкой;

.

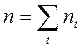Пример: Контракт предусматривает следующий порядок начислений процентов: в первый год – 16%, в каждом последующем полугодии ставка повышается на 1%. Необходимо определить множитель наращения за 2,5 года.