Влияние инфляции на ставку процента
Сначала рассмотрим суть явления инфляции на примере стоимости потребительской корзины, которая включает в себя N видов товаров (продовольственных и непродовольственных) и услуг. Количество единиц товаров 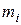 каждого вида (
каждого вида ( 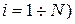 необходимых на некоторый срок t также утверждено в составе продовольственной корзины. Предположим, что в некоторый момент времени t0 цены за единицу каждого вида товара были равны
необходимых на некоторый срок t также утверждено в составе продовольственной корзины. Предположим, что в некоторый момент времени t0 цены за единицу каждого вида товара были равны 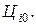 Тогда стоимость потребительской корзины можно определить по формуле:
Тогда стоимость потребительской корзины можно определить по формуле:
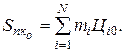
По истечению некоторого времени t - t0 цены на некоторые товары могут измениться как в сторону увеличения, так и в сторону уменьшения. Предположим, что в момент времени t цены имеют значения 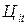 . Стоимость потребительской корзины в момент времени t определится аналогичной формулой:
. Стоимость потребительской корзины в момент времени t определится аналогичной формулой:
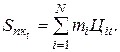
Если 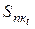 >
> 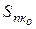 , то говорят о явлении инфляции, если
, то говорят о явлении инфляции, если 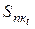 <
< 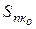 , то говорят о явлении дефляции. Как правило, по истечению некоторого интервала времени t - t0 (месяц, квартал, год) стоимость потребительской корзины увеличивается из-за увеличения цен на товары, т. е. наблюдается явление инфляции. Увеличение стоимости потребительской корзины можно записать в виде
, то говорят о явлении дефляции. Как правило, по истечению некоторого интервала времени t - t0 (месяц, квартал, год) стоимость потребительской корзины увеличивается из-за увеличения цен на товары, т. е. наблюдается явление инфляции. Увеличение стоимости потребительской корзины можно записать в виде
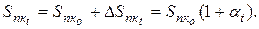 (1.20)
(1.20)
Величину 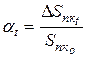 называют темпом или уровнем инфляции. Данные об уровне инфляции
называют темпом или уровнем инфляции. Данные об уровне инфляции 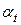 за каждый календарный месяц прошедших лет можно просто найти в Интернете.
за каждый календарный месяц прошедших лет можно просто найти в Интернете.
Но явление инфляции можно рассматривать с другой точки зрения. Предположим, что в момент времени t0 у меня имелась сумма денежных средств 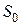 руб. и эта сумма равна стоимости потребительской корзины
руб. и эта сумма равна стоимости потребительской корзины 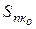 . Через некоторое время t - t0 стоимость потребительской корзины увеличилась из-за инфляции и я за ту же сумму денежных средств
. Через некоторое время t - t0 стоимость потребительской корзины увеличилась из-за инфляции и я за ту же сумму денежных средств 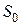 руб. не смогу приобрести весь перечень товаров входящих в потребительскую корзину. То есть явление инфляции проявляется в снижении покупательной способности денежных средств, т. е. денежные средства
руб. не смогу приобрести весь перечень товаров входящих в потребительскую корзину. То есть явление инфляции проявляется в снижении покупательной способности денежных средств, т. е. денежные средства 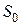 руб. обесцениваются. Их реальная стоимость, определяющаяся покупательной способностью уменьшается и может быть определена по формуле:
руб. обесцениваются. Их реальная стоимость, определяющаяся покупательной способностью уменьшается и может быть определена по формуле:
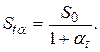 (1.21)
(1.21)
В статистических данных приводятся значения уровня инфляции α за каждый календарный месяц года. Определим уровень инфляции за несколько периодов (месяцев). Пусть темпы инфляции за последовательные периоды времени равны 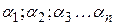 (см. рис. 1.5). Первоначальная сумма денежных средств
(см. рис. 1.5). Первоначальная сумма денежных средств 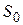 по прошествии первого периода времени t1 с уровнем инфляции
по прошествии первого периода времени t1 с уровнем инфляции 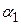 будет иметь реальную стоимость:
будет иметь реальную стоимость:
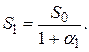

Рис. 1.5. Определение уровня инфляции за несколько периодов
После истечения двух периодов времени реальная стоимость первоначальной суммы денежных средств будет равна:
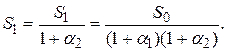 (1.22)
(1.22)
Для реальной стоимости денежных средств после истечения n периодов времени, по аналогии с формулой (1.22), можно записать:
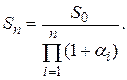 (1.23)
(1.23)
Суммарный уровень инфляции за все n периодов должен давать такую же реальную стоимость денежных средств, как и формула (1.23):
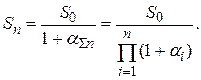
Отсюда для суммарного уровня инфляции за n периодов получим:
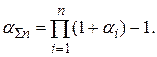 (1.24)
(1.24)
Введем понятие среднего за период уровня инфляции. Если интервалы ti равны, например, одному месяцу; а n = 12, то будем говорить о среднегодовом уровне инфляции 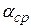 . При таком подходе можно считать уровень инфляции во всех месяцах года постоянным; равным среднегодовому
. При таком подходе можно считать уровень инфляции во всех месяцах года постоянным; равным среднегодовому 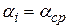 . С учетом данного равенства формулу (1.23) можно записать в виде:
. С учетом данного равенства формулу (1.23) можно записать в виде:
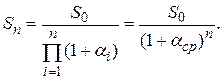
Из этого равенства для среднегодового уровня инфляции получим формулу:
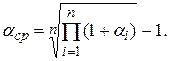 (1.25)
(1.25)
Оценим вначале влияние инфляции на годовую процентную ставку. При первоначальной сумме 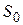 наращенная сумма
наращенная сумма 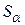 через один год с учетом инфляции может быть определена по формуле:
через один год с учетом инфляции может быть определена по формуле:
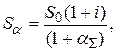 (1.26)
(1.26)
где 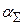 - суммарный годовой уровень инфляции, определяемый по формуле (1.24) по данным о ежемесячном уровне инфляции
- суммарный годовой уровень инфляции, определяемый по формуле (1.24) по данным о ежемесячном уровне инфляции 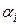 .
.
Формула (1.26) может быть преобразована к виду:
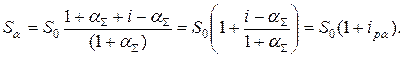
Из последнего равенства можно записать формулу для реально действующей в условиях инфляции годовой процентной ставки доходности 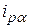
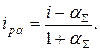 (1.27)
(1.27)
На рис. 1.6 приведены графики зависимости реальной готовой процентной ставки от суммарного годового уровня инфляции. Из приведенных графиков и формулы (1.27) видно, что реальная годовая процентная ставка доходности 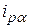 будет положительной только тогда, когда уровень инфляции меньше годовой процентной ставки
будет положительной только тогда, когда уровень инфляции меньше годовой процентной ставки 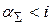 . При
. При 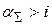 несмотря на вложение денежных средств с обещанной доходностью i % фактически первоначальная вложенная сумма
несмотря на вложение денежных средств с обещанной доходностью i % фактически первоначальная вложенная сумма 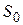 будет обесцениваться.
будет обесцениваться.
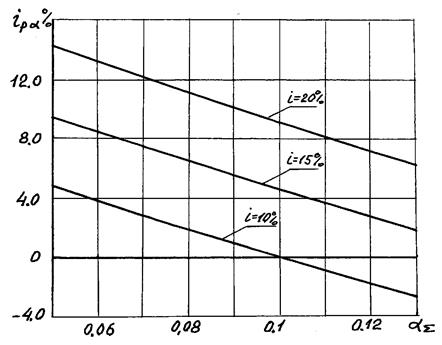
Рис. 1.6. Зависимость реальной процентной ставки от уровня инфляции
Часто возникает обратная задача, определить под какую годовую процентную ставку i нужно разместить денежные средства, чтобы через год при заданном годовом уровне инфляции αΣ получить желаемое значение реально действующей, с учетом инфляции, процентной ставки ipα. При такой постановке в формуле (1.27) известными являются величины αΣ и ipα, а определить нужно i.
В результате преобразований формулы (1.27) получим
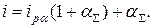
1) Определим реально действующую процентную ставку с учетом инфляции при вложении денежных средств на депозитный договор сроком на n-месяцев при ежемесячном начислении процентов по схеме простых процентов.
При начислении простых процентов наращенную сумму 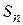 с учетом данных о ежемесячной инфляции
с учетом данных о ежемесячной инфляции 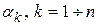 можно определить по формуле:
можно определить по формуле:
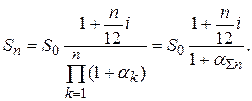
По аналогии с формулой (1.27) можно получить реальную, действующую с учетом инфляции, доходность выше оговоренной финансовой операции по вложению суммы 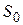 на депозит
на депозит
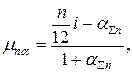 (1.28)
(1.28)
где 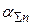 - суммарный уровень инфляции за n месяцев депозитного договора.
- суммарный уровень инфляции за n месяцев депозитного договора.
Поставим обратную задачу. Определим, при какой годовой процентной ставке по депозитному договору доходность данной финансовой операции будет не меньше чем 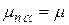 . Из формулы (1.28) получим:
. Из формулы (1.28) получим:
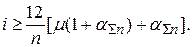 (1.29)
(1.29)
Из формулы (1.29) следует, что для получения реальной доходности 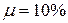 при вложении денежных средств на депозитный договор на срок 12 месяцев при суммарной годовой инфляции
при вложении денежных средств на депозитный договор на срок 12 месяцев при суммарной годовой инфляции 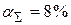 годовая процентная ставка по депозиту должна быть не меньше 18,8%.
годовая процентная ставка по депозиту должна быть не меньше 18,8%.
2) Определим реально действующую процентную ставку с учетом инфляции при вложении денежных средств 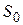 на депозитный договор на n месяцев при ежемесячном начислении процентов по схеме сложных процентов.
на депозитный договор на n месяцев при ежемесячном начислении процентов по схеме сложных процентов.
Наращенную сумму 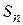 с учетом данных о ежемесячной инфляции
с учетом данных о ежемесячной инфляции 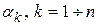 можно определить по формуле:
можно определить по формуле:
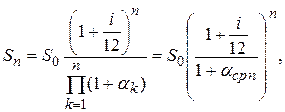
где 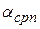 - средний за период n месяцев уровень ежемесячной инфляции определяемой по формуле (1.25).
- средний за период n месяцев уровень ежемесячной инфляции определяемой по формуле (1.25).
Определяя реальную доходность вложения денежных средств на депозит на n месяцев по схеме сложных процентов можно записать:
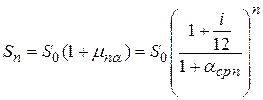
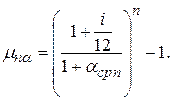 (1.30)
(1.30)
Определим, при какой годовой процентной ставке по депозитному договору на n месяцев при ежемесячном начислении процентов доходность данной финансовой операции с учетом инфляции будет не меньше чем 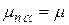 . Из формулы (1.30) получим:
. Из формулы (1.30) получим:
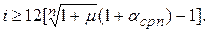 (1.31)
(1.31)
Определим значение i при 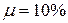 . При суммарной годовой инфляции
. При суммарной годовой инфляции 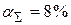 среднемесячный уровень инфляции будет равен
среднемесячный уровень инфляции будет равен 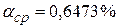 . Тогда при вложении денежных средств на депозит на 12 месяцев с ежемесячным начислением процентов по схеме сложных процентов годовая процентная ставка по депозиту должна быть не меньше 17,5%.
. Тогда при вложении денежных средств на депозит на 12 месяцев с ежемесячным начислением процентов по схеме сложных процентов годовая процентная ставка по депозиту должна быть не меньше 17,5%.
