Вопрос 2. Расчеты при начислении простых процентов
Простые процентные вычисления применяются в финансовых обязательствах, как правило, на срок не более года. При простых процентах расчёты производятся исходя из постоянной базы, в качестве которой выступает первоначальная сумма долга. При заключении договора займа стороны договариваются о размере процентов. Существуют различные методы начисления и присвоения процентов.
Процентной ставкой называется отношение суммы процентных денег, выплачиваемых в единицу времени к величине займа. Ставка выражается в виде десятичной или натуральной дроби или в процентах. Если за базу начисления процентов берется первоначальная сумма долга и начисленные проценты присоединяются к этой сумме в конце срока займа, то для расчета применяется ставка процентов. Примерами являются начисление процентов за кредит, за вклад в сберкассе, на счет в банке. Если при начислении процентов за основу берется сумма, которая уплачивается должником, в этом случае применяется учетная ставка и проценты удерживаются при выдаче ссуды. Интервал времени между начислениями процентов называют периодом начислении.
Наращенная сумма (S) представляет собой первоначальную её сумму вместе с начислениями на неё процентами к концу срока. Она определяется путём умножения начальной суммы на множитель наращивания. Наращенная сумма (формула простых процентов) рассчитывается следующим образом:
,
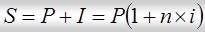гдеS – наращенная сумма долга;
Р – первоначальная сумма долга;
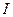– проценты за весь срок ссуды;
n– общийсрок ссуды(число периодов начисления);
i – ставка процентов за период;
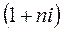– множитель наращивания простых процентов.
Величина процентной ставки исчисляется по формуле:
.
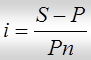Если величина расчетного периода принимается за 360 дней, то такие проценты называются обыкновенными или коммерческими; если 365 дней – то точными.
При сроке ссуды менее года необходимо определить, какая часть годового процента уплачивается кредитору. Выразим величину n в виде дроби:
,
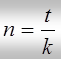где t – число дней ссуды;
k – число дней в году или временная база.
Тогда наращенная сумма примет следующий вид:
.
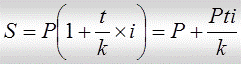Из данной формулы выразим срок ссуды:
.
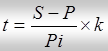Тогда величина процентной ставки будет определяться по формуле:
.
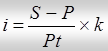В том случае, если ставка процентов меняется во времени, наращенная сумма будет рассчитываться по формуле:
,
где i – ставка простых процентов в периоде r;
n – продолжительность периода.
Настоящая (приведенная, текущая) стоимость денег представляет собой сумму будущих денежных поступлений, приведенных с учетом определенной ставки процента (дисконтной ставки) к настоящему периоду. Определение настоящей стоимости денег связано с процессом дисконтирования этой стоимости, который представляет собой операцию, обратную наращению. Такая ситуация возникает в тех случаях, когда определяют, сколько средств необходимо инвестировать сегодня для того, чтобы через определенное время получить заранее обусловленную их сумму.
При расчете суммы простых процентов в процессе дисконтирования стоимости денежных средств (т.е. суммы дисконта) используется следующая формула:
P = S/ (1 + ni),
Множитель 1/(1 + ni) называется дисконтным коэффициентом простых процентов, значение которого всегда должно быть меньше единицы.
