Портфель максимальной эффективности при заданном его риске
Рассмотрим портфель состоящий из двух видов бумаг. Задача нахождения структуры портфеля 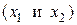 , обеспечивающих его максимальную эффективность при заданном риске может быть записана в виде:
, обеспечивающих его максимальную эффективность при заданном риске может быть записана в виде:
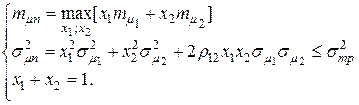 (4.31)
(4.31)
Из второго уравнения (4.31) можно определить две пары значений 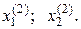 Для этого сделаем замену переменной
Для этого сделаем замену переменной 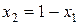
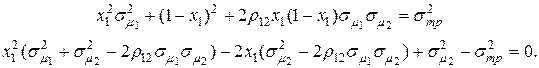
Из решения данного уравнения находим:
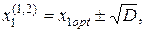 (4.32)
(4.32)
где:
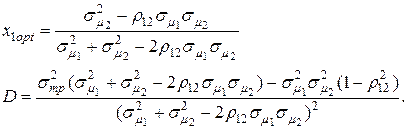 (4.33)
(4.33)
Значения 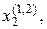 находим из условия:
находим из условия:
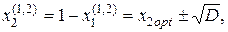
где 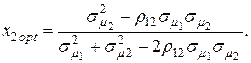 (4.34)
(4.34)
При значениях 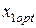 и
и 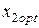 риск портфеля ценных бумаг будет минимальным (см. рис.4.2). При значениях ценовых долей бумаг первого и второго вида:
риск портфеля ценных бумаг будет минимальным (см. рис.4.2). При значениях ценовых долей бумаг первого и второго вида:
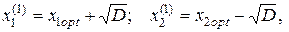 (4.35)
(4.35)
а также при
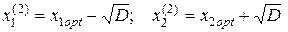 (4.36)
(4.36)
риск портфеля ценных бумаг 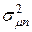 будет равен заданному значению
будет равен заданному значению 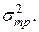
Второе неравенство в (4.31) будет выполняться, когда значения 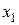 и
и 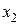 будут соответствовать условиям:
будут соответствовать условиям:
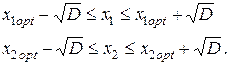
Из рис. 4.1а видно, что эффективность портфеля ценных бумаг двух видов 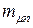 изменяется линейно при изменении
изменяется линейно при изменении 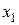 от 0 до 1. Из этого следует, что в зависимости от соотношения значений
от 0 до 1. Из этого следует, что в зависимости от соотношения значений 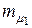 и
и 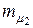 портфель максимальной эффективности при заданном риске обеспечивается при структуре портфеля, определяющейся формулами (4.35) или (4.36).
портфель максимальной эффективности при заданном риске обеспечивается при структуре портфеля, определяющейся формулами (4.35) или (4.36).
Пример 4.4. Портфель ценных бумаг состоит из двух видов коррелированных (зависимых) бумаг со следующими значениями эффективности и риска 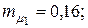
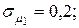
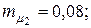
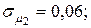
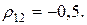 Определить структуру портфеля ценных бумаг максимальной эффективности при заданном его риске
Определить структуру портфеля ценных бумаг максимальной эффективности при заданном его риске 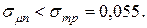
Решение. Определим значение 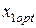 и
и 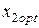 , при которых обеспечивается минимальный риск портфеля ценных бумаг:
, при которых обеспечивается минимальный риск портфеля ценных бумаг:
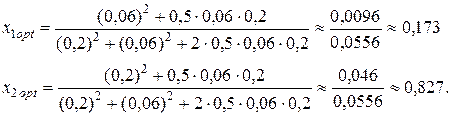
Определим минимальное значение риска портфеля ценных бумаг и его эффективность:
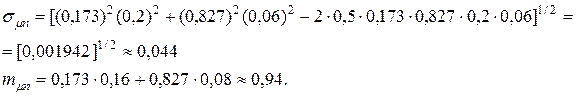
Определим значение дискриминанта D:
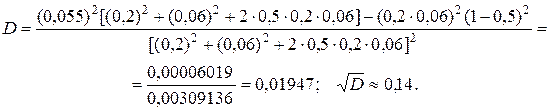
По формулам (4.35) и (4.36) определяем границы интервалов возможных значений ценовых долей бумаг:
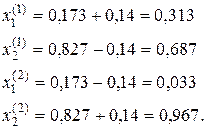
Определим риск и эффективность портфеля ценных бумаг при 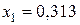 и
и 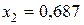
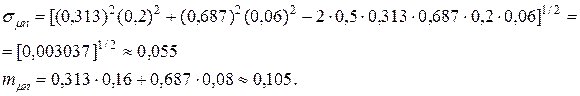
При ценовых долях бумаг 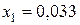 и
и 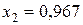 для риска и эффективности портфеля ценных бумаг получим значение:
для риска и эффективности портфеля ценных бумаг получим значение:
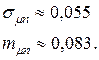
Из приведенных расчетов следует, что портфель максимальной эффективности при заданном риске обеспечивается при ценовых долях ценных бумаг равных 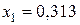 и
и 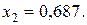 При этом эффективность портфеля равна
При этом эффективность портфеля равна 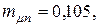 а риск определяемый коэффициентом вариации будет равен
а риск определяемый коэффициентом вариации будет равен 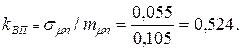
Для оптимального портфеля по критерию минимума среднеквадратического отклонения доходности портфеля 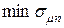 при
при 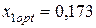 и
и 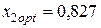 эффективность портфеля равна
эффективность портфеля равна 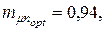 а риски оцениваемые коэффициентом вариации равны
а риски оцениваемые коэффициентом вариации равны 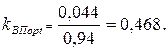 Таким образом, переход от оптимального по
Таким образом, переход от оптимального по 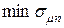 портфеля к портфелю с максимальной эффективности увеличивает риски по коэффициенту вариации в
портфеля к портфелю с максимальной эффективности увеличивает риски по коэффициенту вариации в 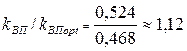 раз. Но эффективность портфеля также возрастает
раз. Но эффективность портфеля также возрастает 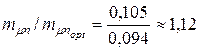 раз.
раз.
Контрольные вопросы и задания
1. Виды ценных бумаг.
2. Характеристики ценных бумаг и их классификация.
3. Доходность ценной бумаги. Нарицательная стоимость (номинал) и рыночная стоимость ценной бумаги.
4. Доходность портфеля ценных бумаг.
5. Доходность и риск ценной бумаги в условиях изменения ее рыночной стоимости. Эффективность ценной бумаги и портфеля ценных бумаг. Количественная оценка риска портфеля ценных бумаг.
6. Портфель из двух видов ценных бумаг. Зависимость эффективности 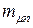 ,
, 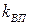 от ценовой доли бумаг х1 при ρ = 0.
от ценовой доли бумаг х1 при ρ = 0.
7. Зависимость показателей риска портфеля из двух видов ценных бумаг 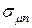 ,
, 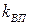 от коэффициента корреляции бумаг первого и второго вида.
от коэффициента корреляции бумаг первого и второго вида.
8. Определить оптимальное распределение ценовых долей бумаг первого и второго вида х1 и х2, обеспечивающие минимум среднеквадратического значения рисков 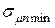 портфеля бумаг двух видов, при следующих значениях их доходностей и рисков
портфеля бумаг двух видов, при следующих значениях их доходностей и рисков 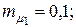
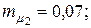
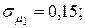
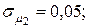
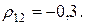
Для вычисленных значений х1 и х2 определить эффективность 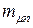 и показатель риска
и показатель риска 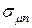 и
и 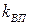 портфеля ценных бумаг.
портфеля ценных бумаг.
9. Определить оптимальное распределение ценовых долей бумаг первого и второго вида х1 и х2, обеспечивающие минимум коэффициента вариации 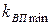 портфеля бумаг двух видов, при следующих значениях их доходностей и рисков
портфеля бумаг двух видов, при следующих значениях их доходностей и рисков 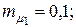
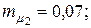
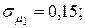
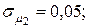
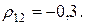
Для вычисленных значений х1 и х2 определить эффективность 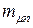 и показатель риска
и показатель риска 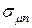 и
и 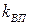 портфеля ценных бумаг. Сравнить результаты вычисления
портфеля ценных бумаг. Сравнить результаты вычисления 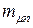 ;
; 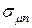 и
и 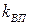 в заданиях 8 и 9, сделать выводы.
в заданиях 8 и 9, сделать выводы.
10. Для портфеля из четырех видов независимых ценных бумаг со средними доходностями 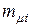 и рисками
и рисками 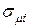 соответственно равными
соответственно равными
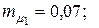
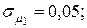
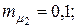
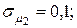
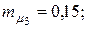
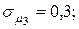
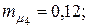
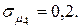
Найти оптимальную структуру портфеля (х1; х2; х3; х4) минимального риска. Для оптимальной структуры портфеля определить значения 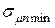 и
и 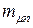 .
.
11. Определить стоимостные доли х1 и х2 портфеля ценных бумаг двух видов, обеспечивающие минимальный риск портфеля при заданной его эффективности 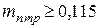 , если эффективность и риск бумаг первого и второго вида соответственно равны
, если эффективность и риск бумаг первого и второго вида соответственно равны 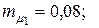
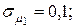
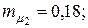
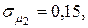 при двух значениях коэффициента корреляции ценных бумаг
при двух значениях коэффициента корреляции ценных бумаг 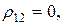
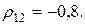
12. Для портфеля, состоящего из трех видов независимых ценных бумаг, эффективность и риск которых имеют соответственно значения 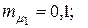
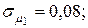
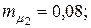
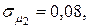
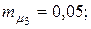
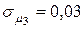 . Определить структуру портфеля ценных бумаг х1, х2, х3 обеспечивающую минимальный риск портфеля
. Определить структуру портфеля ценных бумаг х1, х2, х3 обеспечивающую минимальный риск портфеля 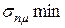 при его заданной эффективности
при его заданной эффективности 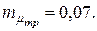
13. Для портфеля, состоящего из двух видов зависимых бумаг со следующими значениями эффективности риска 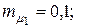
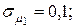
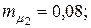
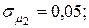
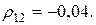 определить структуру портфеля ценных бумаг максимальной эффективности при заданном риске портфеля
определить структуру портфеля ценных бумаг максимальной эффективности при заданном риске портфеля 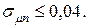
Облигации
Основные понятия и характеристики доходности облигаций
Облигация – это ценная бумага, обеспечивающая ее обладателю оговоренный доход, в связи с предоставлением обладателем облигации ее эмитенту займа на фиксированный, как правило, длительный срок. Облигации являются эмиссионными ценными бумагами, выпускаемыми эмитентом для заимствования денежных средств. Эмитентами облигаций могут быть государство (федеральные или региональные органы исполнительной власти), муниципалитеты, корпорации, финансовые или коммерческие учреждения.
Доход по облигациям обычно ниже, чем доход по другим ценным бумагам, но в то же время он более стабилен, так как облигацией гарантируется выплата ее владельцу определенная сумма денег на дату ее погашения. Эта сумма денег называется номинальной стоимостью облигации, которая обычно указывается на облигации. Кроме номинальной стоимости облигации характеризуются следующими параметрами:
- дата выпуска облигации 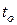 ;
;
- время обращения облигации с момента ее выпуска Т;
- дата погашения 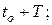
- срок до погашения облигации 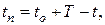 где t – текущая дата;
где t – текущая дата;
- номинальная стоимость облигации 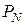 - это сумма денег, выплачиваемая владельцу облигации на дату погашения. Номинальная стоимость обычно указывается на облигации;
- это сумма денег, выплачиваемая владельцу облигации на дату погашения. Номинальная стоимость обычно указывается на облигации;
- выкупная стоимость указывается, если она отличается от номинальной стоимости;
- купонный доход (С) – это постоянные платежи, выплачиваемые владельцу облигации ежегодно по купонной ставке. Купонный доход определяется произведением 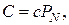 где с – годовая купонная ставка дохода. Если купонные выплаты не предусмотрены, то такую облигацию называют бескупонной.
где с – годовая купонная ставка дохода. Если купонные выплаты не предусмотрены, то такую облигацию называют бескупонной.
