Задания для самостоятельной работы. 1. Измените данные в количестве продаж и получите новый результат

1. Измените данные в количестве продаж и получите новый результат.

2. Проанализируйте изменение решения при сокращении разброса значений цены.

3. Измените функцию тренда и сравните новые параметры с прежними.

4. Выберите различные значения х и сравните получаемые при этом максимальные значения прибыли.

5. Самостоятельно сформулируйте и составьте алгоритм решения оптимизационной задачи на расчет максимальной прибыли.

Лабораторная работа № 6
Тема: Прогнозирование данных. Построение линий тренда и статистический анализ полученных зависимостей

Программное обеспечение:OS Windows, MS Excel, MS Word

Постановка целей занятия:выработать умение графически изображать различные аналитические зависимости, описывать их математическими уравнениями, строить линии тренда, оценивать степень достоверности описания.

На занятии получить с помощью MS Excel различные графические зависимости (с помощью “Мастера диаграмм”), построить на них линии тренда и получить значения коэффициентов корреляции и соответствующих уравнений.

Краткие теоретические сведения:

Линии тренда применяются в задачах прогнозирования, решаемых с использованием методов регрессионного анализа. Регрессионный анализ с помощью линий тренда позволяет оценивать степень корреляции переменных на базе известных значений; продолжить линию зависимости в любом направлении, т.е. экстраполировать ее; выбирать оптимальные механизмы вычисления неизвестных величин.

Получаемые экспериментально зависимости могут быть описаны одним из приближений, задаваемых линиями регрессии (см. табл. 1 ). При этом, правильность выбора аппроксимирующей функции можно определять по значению коэффициента достоверности аппроксимации R². Его максимальное значение равно 1, а при величине в 0,6-0,7 считается, что аппроксимация неудачная.

Поэтому, обычно строят график функции, затем аппроксимируют его линией тренда, определяют наиболее подходящую из примененных и выводят значения коэффициента R². Наконец, после этого находят вид описывающего тренд уравнения и введя в соответствующие ячейки значения x и формулу вычисления y получают значения функции по выбору.

В настоящем задании рассматривается два примера – на построение простейшего графика и его одновариантной аппроксимации, а также выбор наилучшей аппроксимации по R².

Порядок выполнения задания:

1-й этап: задание ряда числовых значений функции для получения ее графического изображения; использование “Мастера диаграмм” для построения исследуемой кривой.

2-й этап: вызов и построение линии тренда; выработка навыков по характеризации тренда – определение значений коэффициента аппроксимации (R²); вызов описывающего тренд уравнения и умение рассчитать значения функции по заданным величинам аргумента.

3-й этап: отработка навыков аппроксимации функций трендами и сравнение их степени совпадения; выбор оптимальных трендов с построением их для вычисления конкретных значений f(x).

4-й этап: выполнение задания самостоятельно и совпадение результатов с данными проверочного задания.

Итак, осуществление первого задания демонстрируется на рис.1-10, а второго, с выбором оптимальных аппроксимаций – на рис.11-27.

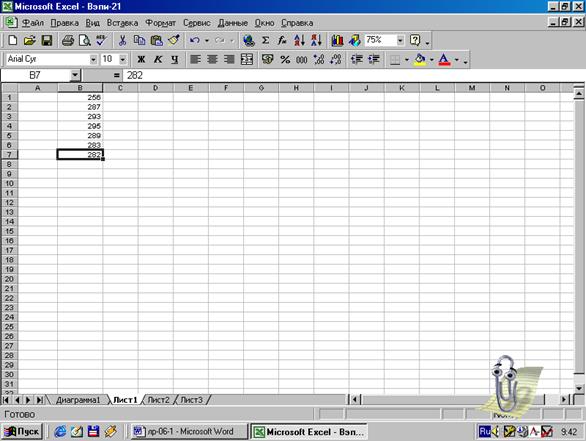
Рис.1.

Задание числовых данных для построения графика

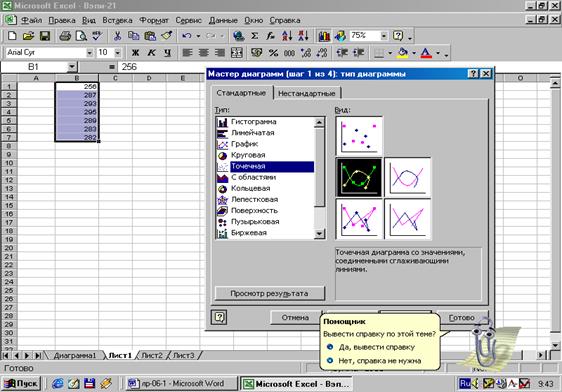
Рис.2.

Применение “Мастера диаграмм” и выбор типа графика

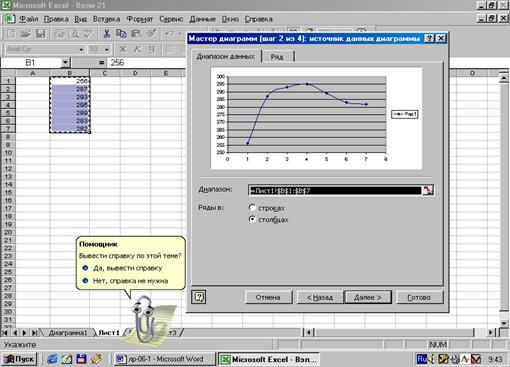
Рис.3.

Построение графика в MS Excel

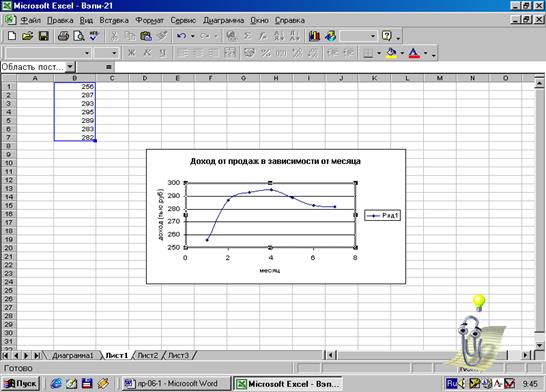
Рис.4.

Вид графика, подвергающегося аппроксимации

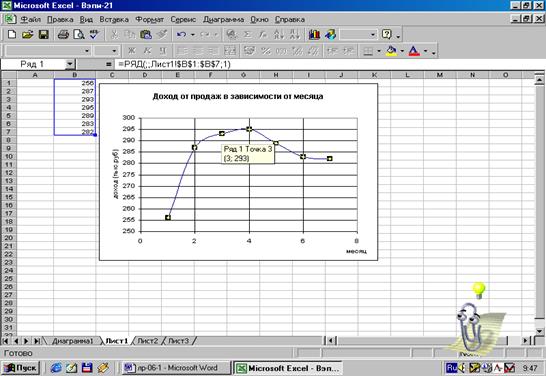
Рис.5.

Активизация графика с целью построения тренда

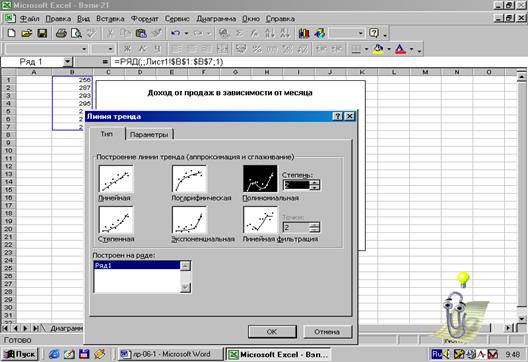
Рис.6.

Выбор типа аппроксимирующей кривой (тренда)

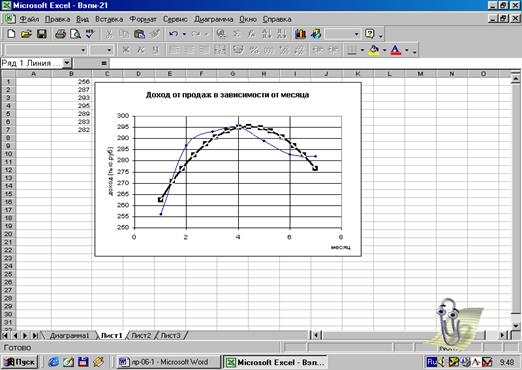
Рис.7.

Вид выбранного тренда на графике функции

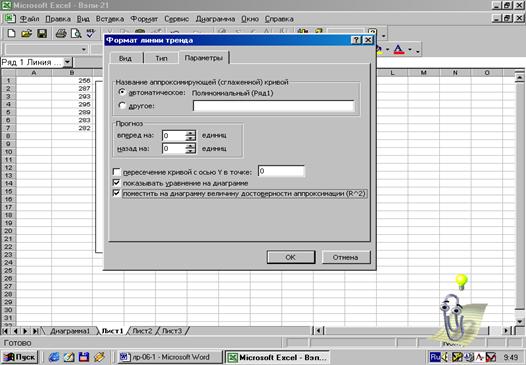
Рис.8.

Задание параметров тренда

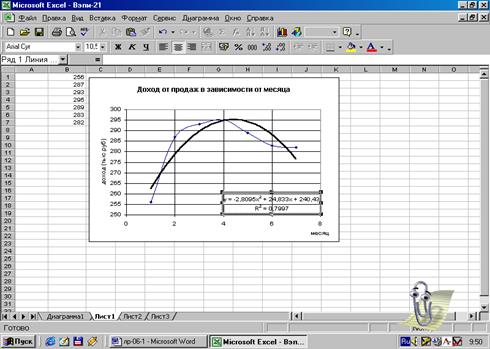
Рис.9.

Вывод в поле функции и тренда значения R² и уравнения

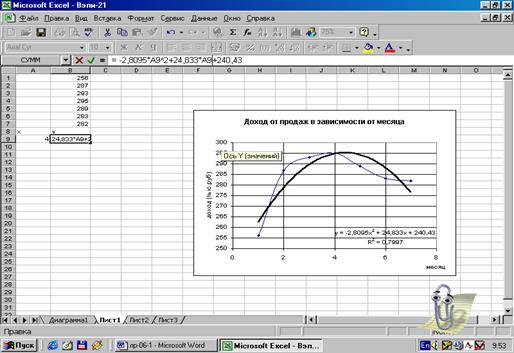
Рис.10.

Определение значений функции с помощью тренда по данным x

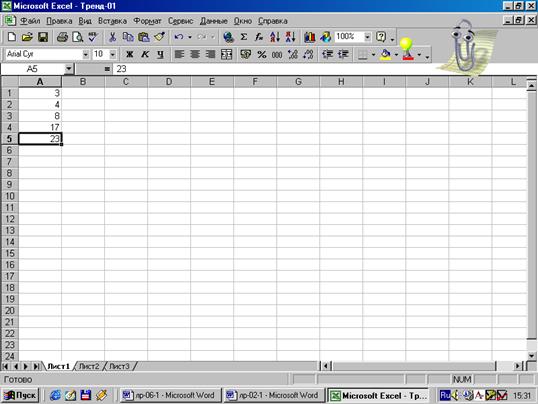
Рис.11.

Численное задание функции

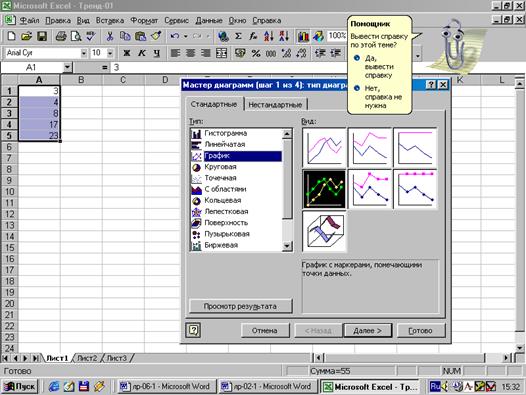
Рис.12.

Построение точечной диаграммы

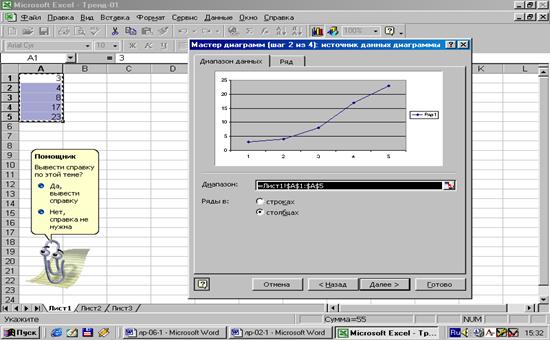
Рис.13.

Вид получаемого графика

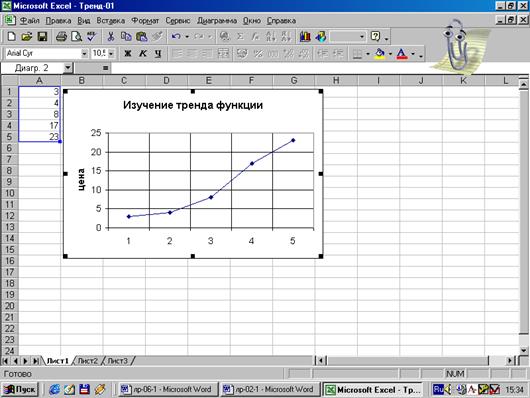
Рис.14.

График функции в поле Excel

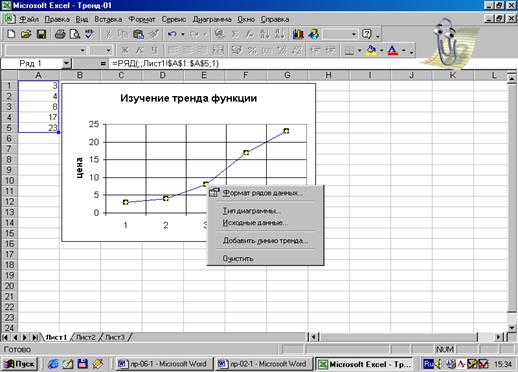
Рис.15.

Вызов линии тренда

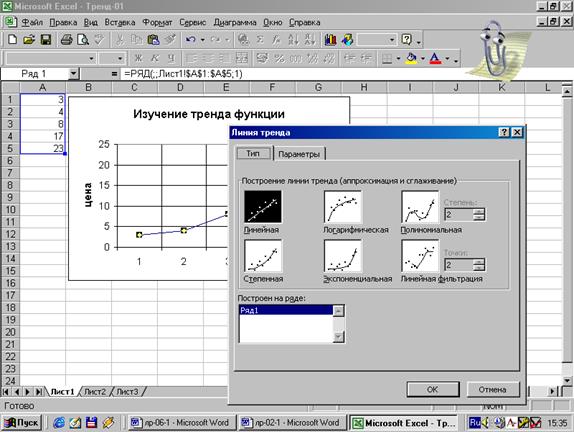
Рис.16.

Выбор аппроксимирующей функции

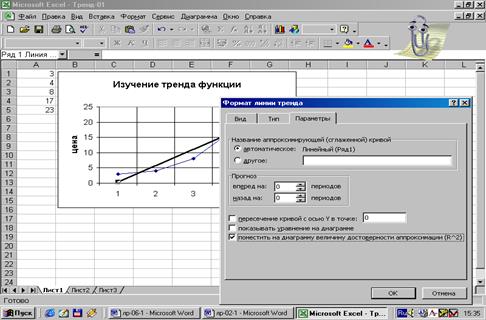
Рис.17.

Определение значения коэффициента аппроксимации

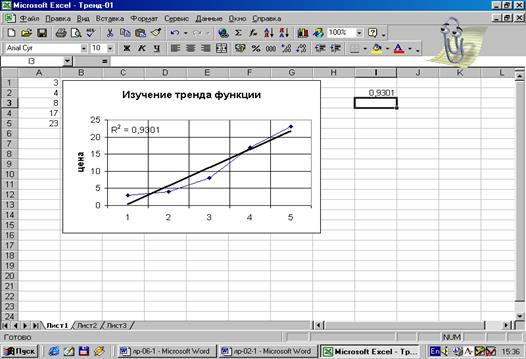
Рис.18.

Результат линейной аппроксимации

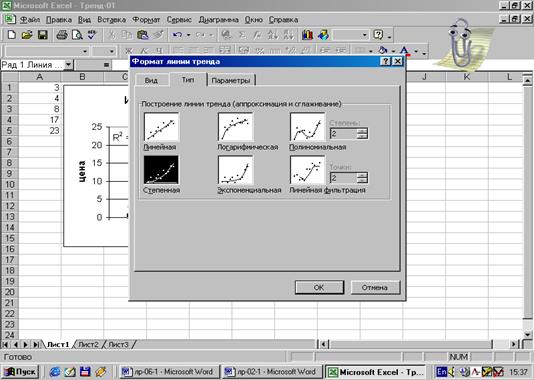
Рис.19.

Степенная аппроксимация

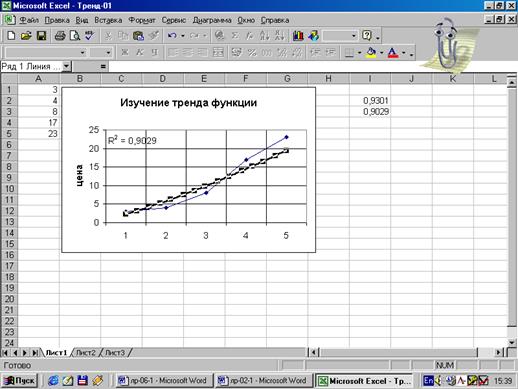
Рис.20.

Результат степенной аппроксимации и ее коэффициент R²

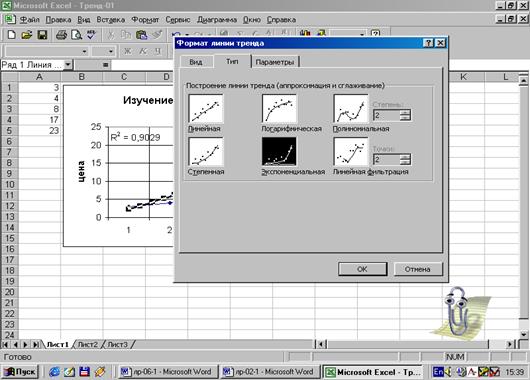
Рис.21.

Логарифмическая аппроксимация

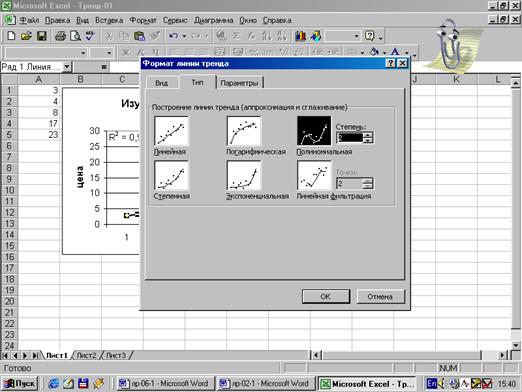
Рис.22.

Полиномиальная аппроксимация (степень 2)

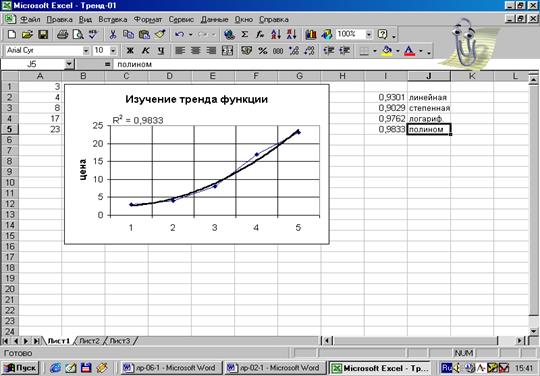
Рис.23.

Результат полиномиальной аппроксимации (степень 2)

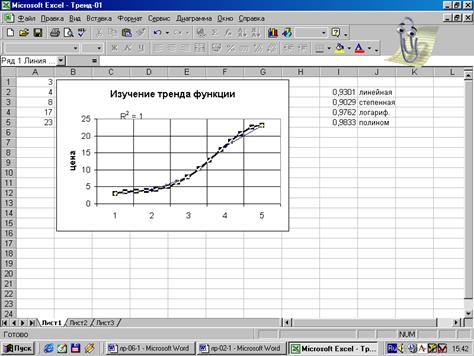
Рис.24.

Результат полиномиальной аппроксимации (степень 4)

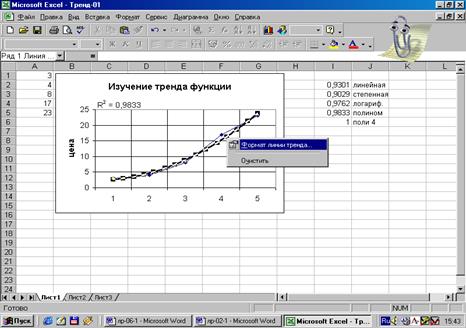
Рис.25.

Активизация линии тренда с целью вызова описывающего уравнения (полином, степень 2)

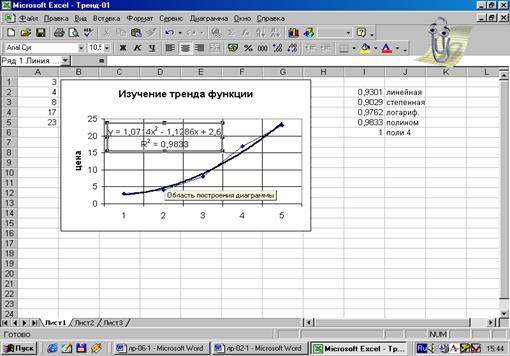
Рис.26.

Внесение параметров тренда в поле графика функции

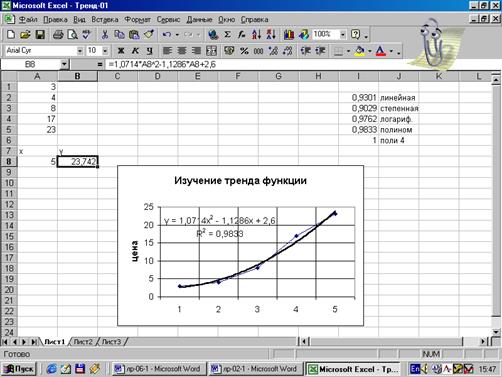
Рис.27.

Использование графика тренда для нахождения значений функции (по заданным величинам x)