Динамические модели 3.1.3.1. Введение

Для динамических моделей характерен учет нескольких периодов. Инвести­ционные объекты характеризуются поступлениями и выплатами, которые ожидаются при реализации этих объектов во времени. Как правило, с этим связано допущение, что существенное влияние альтернатив ограничено посту­плениями и выплатами определенной величины, которые можно спрогно­зировать с отнесением их к определенным срокам. Будем исходить из этого и далее. Преимущественный учет поступлений и выплат, а также исследование динамики показателей по нескольким периодам - это существенные особен­ности, отличающие динамические модели от статических.¹⁹ Сходства состоят

17 18

На этом остановимся также в разделе 5.3.2.

В случае желания учесть выручку от ликвидации в амортизационном расчете открывается возмож­ность оценить значение выручки от ликвидации для отдельных периодов эксплуатации и включить их по этим периодам в расчет срока амортизации. См. Heinhold, M: (Investitionsrechmmg), с. 75.

прежде всего в отношении действенности приведенных в разделе 3.1.1. допу­щений.

В динамических моделях платежи осуществляются в различные сроки. Из-за зависимости размера платежей от срока их осуществления (предпочтение по времени) их нельзя непосредственно суммировать, а необходимо провести финансово-математические преобразования (например, ревальвацию или дис­контирование). Поэтому во введении ознакомимся с основами финансовой математики²⁰.

При этом сначала рассмотрим начисление процентов на процент (сложных процентов). При ревальвации определяют, какую стоимость (W) будет иметь инвестированная к определенному моменту времени сумма капитала (здесь момент времени равен 0) в более поздний момент времени (t) с учетом на­числения процентов и сложных процентов. Если процентная ставка (i) для всех периодов (здесь время исчисляется в годах) между моментами 0 и t одинакова, то показатель W определяется следующим образом²¹:

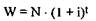
Следовательно, при ревальвации капитала в размере 10.000 ЕВРО, инвести­рованного по ставке 10% (=0,1), его стоимость составит через три года:

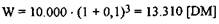
Величина (1+Г)¹, на которую должна быть умножена сумма инвестируемого капитала при ревальвации, называется коэффициентом ревальвации. Для его обозначения принят символ q^l (где q=l+i).

Если процентные ставки одинаковы не для всех периодов, то для каждого периода t определяется отдельный коэффициент (l+i_t или q_t). При ревальва­ции сумма инвестируемого капитала умножается на все коэффициенты, рас­считанные для каждого периода. Стоимость капитала через Т периодов вы­числяется следующим образом:

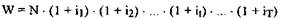
Если в вышеприведенном примере процентные ставки составляют ,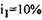

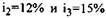при прочих неизменных данных, то стоимость капитала в результате ревальвации составит:

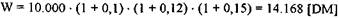
Дисконтирование служит для расчета стоимости (W), которая должна быть инвестирована в какой-либо момент времени (здесь он равен 0), с тем чтобы в будущем (момент t) иметь в распоряжении определенную сумму (N). Дискон-

звание осуществляется по сходной с ревальвацией форме. При одинаковой |вовсех периодах процентной ставке значение W в нулевой момент времени (рассчитывается по формуле:

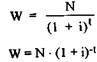или

Обозначение 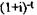(или 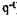) представляет собой коэффициент дисконти-

рования. В нашем примере в результате дисконтирования 10.000 ЕВРО с момен­та времени 3 на-момент времени 0 по ставке 10% получаем:

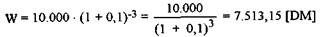
Дисконтирование при различных ставках процента в рассматриваемых периодах осуществляется аналогично ревальвации с помощью рассчитанных для каждого периода коэффициентов дисконтирования.

В динамических инвестиционных расчетах необходимо провести перерас­чет ряда платежей одинакового размера в единую величину с учетом процен­тов и начисления процента на процент. Это можно осуществить с помощью расчета периодических поступлений.

Для подсчета фактической стоимости, т.е. вычисления стоимости в мо­мент времени О (W) для ряда платежей одинакового размера (N), которые еже­годно осуществляются в конце каждого года в течение t лет, используется формула:

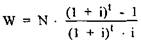
Коэффициент, на который умножается сумма платежа, называется коэффи­циентом фактической стоимости периодических поступлений. Если через 3 года ежегодно производятся платежи в размере 10.000 ЕВРО, то их фактическая стоимость по ставке 10% составит:

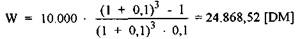
Подобным образом можно произвести расчет периодических поступлений путем преобразования имеющейся на нулевой момент времени стоимости (N) в ряд отнесенных на конец года платежей (W) равной величины, которые осуществляются до момента t:

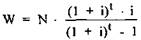По вопросам финансовой математики см. Kahle, E.; Lohse, D.: (Gnmdkurs); Caprano, E.; Gierl, A.: (Finanzmathematik).

Здесь и в нижеследующем закладывается начисление процентов с доплатой, т.е. имеющийся в наличии к началу периода капитал служит в качестве величины для расчета процентов. См. Kruschwitz, L.: (Finanzmathematik), с. 3.

Использованный при перерасчете коэффициент называется коэффициен­том восстановления. Он представляет собой величину, обратную коэффи­циенту фактической стоимости периодических поступлений. Модифицировав вышеупомянутый пример, в результате получим следующий размер периоди­ческих поступлений, на которые разложена сумма 10.000 ЕВРО:

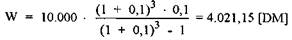
Во введении следует также выделить различные виды инвестиций по структуре платежей. К инвестициям первого типа (собственным инвестициям) Е.ШНАЙДЕР относит вложения, при которых выплаты "в целом"²² произво­дятся перед поступлениями²³.

Он уточняет это высказывание в том смысле, что при соответствующих инвестициях время выплат предшествует времени поступлений. В случае ин­вестиций второго типа это происходит в обратной последовательности²⁴ .

Время выплат или поступлений - это такой момент, когда стоимость ре­вальвируемых или дисконтируемых на этот момент платежей равна сумме объемов платежей (совокупной стоимости платежных сумм)²⁵.

Особой формой собственных инвестиций являются нормальные инвести­ции, при которых за выплатами следуют только поступления, т.е. поступления превышают платежи²⁶.

Далее в соответствии с понятием инвестиций, определяемых платежами, рассмотрим инвестиции первого типа. Подробнее остановимся также на поня­тии нормальных инвестиций.

Динамические модели оценки выгодности можно подразделить на две груп­пы. В моделях первой группы предполагается существование совершенного рынка капитала. В этом случае платежи ревальвируются или дисконтируются по единой расчетной ставке процента. Напротив, в моделях второй группы предполагается, что процентные ставки при вложении и привлечении финан­совых средств отличаются друг от друга.

Различные методы анализа моделей обеих групп различаются прежде всего в отношении принимаемой в расчет целевой функции. На нижеследующей схеме представлен обзор динамических методов оценки выгодности, а также указано, в каком разделе рассматривается каждый из них.

²² Schneider, E.: (Wirtschaftlichkeitsrechnung), с. 9.

²³ Liicke, W.: (Investitionslexikon), с. 152.

²⁴ Schneider, E.: (Wirtschaftlichkeitsrechnung), с. 9.

²⁵ Lucke, W.: (Investitionslexikon), c. 421.

²" Kruschwitz, L.: (Investitionsrechnung), c. 95. О подобном определении понятия "нормальные инвес­тиции", касающегося также и не собственно инвестиций, см. Schneider, E.: (Wirtschaftlich-keitsrechmmg), c. 21.

3.1.3.2. Метод определения стоимости капитала

Описание метода

Метод определения стоимости капитала служит для оценки инвестицион­ных альтернатив относительно монетарной целевой функции "стоимость ка­питала".

Стоимость капитала - это сумма всех дисконтируемых или револьвируемых на какой-либо момент времени поступлений и выплат, возникших в результате реализации инвестиционного объекта.

В модели определения стоимости капитала предполагается существование совершенного рынка капитала. Существующая на этом рынке единая расчет­ная процентная ставка, по которой финансовые средства могут быть инвес­тированы или привлечены в неограниченном размере, служит для ревальва­ции или дисконтирования платежей.

Часто стоимость капитала относится к началу планового периода, т.е. к мо­менту времени непосредственно перед первыми платежами. Из этого будем исходить и далее. В этом случае стоимость капитала представляет собой сумму всех дисконтируемых на этот момент платежей, вызванных реализа­цией объекта инвестирования. При этом она представляет собой фактическую стоимость, которую можно охарактеризовать как прирост имущества в денеж-

Busse von Colbe, W.; LaBmami, G.: (Betriebswirtschaflstheorie), c. 47.

ной форме, приносимый инвестиционным объектом в начале планового пе­риода с учетом процентов²⁸.

При использовании метода определения стоимости капитала применяются следующие правила оценки выгодности инвестиционных объектов²⁹: