Цели и ограничения в инвестиционном проектировании
Системы целей в инвестиционном проектировании, как правило, имеют иерархическую структуру и содержат процедуры поиска компромиссных решений, согласующих цели основных участников проекта.
Цель инвестиций являются сложным объектом, который можно представить в виде логического дерева. В вершинах этого дерева располагаются логические конструкции для проверки условий достижения или достижимости локальных целей. Формализованное представление таких конструкций осуществляется на различных уровнях инвестиционной деятельности. На практике системы целей позволяют сформировать и обосновать рациональные инвестиционные решения.
Каждая система целей является результатом преобразования другой абстрактной системы, которая может представляться и в неформализованном виде.
Основой построения инвестиционной модели для оптимизации являются:
Ø применение в качестве ее составляющих отработанные модели-модули,
Ø учета инвестиционных ресурсов и рисков с помощью целевой функции или ограничений,
Ø отражения логических ограничений инвестиционных решений.
Успех инвестиционного проекта характеризуется векторным индикатором, каждая составляющая которого принимает значения из некоторого множества значений. Для принятия детерминированных решений обычно используется двузначная логика. Для формализации составляющей успеха в инвестиционный цикл по каждому критерию эффективности достижимость инвестиционных целей можно представить следующим образом:
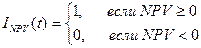 (3.1)
(3.1)
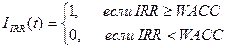 (3.2)
(3.2)
где WACC - средневзвешенная стоимость заемного капитала.
Заметим, что уже в этих простых формализациях присутствие фактора времени t требует перехода к вероятностному представлению успеха. Вероятностное представление успеха инвестиционного цикла проводится с помощью математического ожидания от произведения индикаторов, которые являются случайными функциями времени, следующего вида:
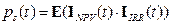 , (3.3)
, (3.3)
где 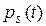 - достигнутая для времени t вероятность успеха инвестиционного цикла. Здесь успех инвестиционного проекта интерпретируется, как одновременное достижение положительной рентабельности проекта и способности инвестора возвратить кредиторам заемные средства.
- достигнутая для времени t вероятность успеха инвестиционного цикла. Здесь успех инвестиционного проекта интерпретируется, как одновременное достижение положительной рентабельности проекта и способности инвестора возвратить кредиторам заемные средства.
Исследователи инвестиционного цикла, как субъекты капиталовложений, для обеспечения своих долгосрочных выгод заинтересованы в обеспечении своего успеха. Формализация успеха исследователя имеет свои особенности. Поток доходов исследователей зависит от инвестиций в исследовательскую деятельность. Происходит обучение заказчиков и разработчиков ТЭО, а также отработка бизнес-планов в соответствии с опытом реализации проектов.
Для оценки технико-экономической реализуемости инвестиционного проекта необходимо принимать всю совокупность ограничений, включая показатели безубыточности и ограничения на ресурсы исследователей. Достоверные оценки исследователей проектов способны воздействовать на эффективность инвестиций.
3.2. Финансовая реализуемость инвестиционных проектов
(Оптимизация в условиях ограниченности финансовых ресурсов)
Цель определения схемы финансирования – обеспечение финансовой реализуемости инвестиционного проекта, т.е. обеспечение такой структуры денежных потоков проекта, при которой на каждом шаге расчета имеется достаточное количество денег для его продолжения. Если не учитывать неопределенность и риск, то достаточным условием финансовой реализуемости инвестиционного проекта является неотрицательность на каждом шаге величины накопленного сальдо потока.
При разработке схемы финансирования определяется потребность в привлеченных средствах. При необходимости возможно вложение части положительного сальдо суммарного денежного потока на депозиты или в долговые ценные бумаги. Такие вложения называются вложением в дополнительные фонды или новое инвестиционное предложение.
В дополнительные фонды могут включаться средства из амортизации и чистой прибыли. Включение средств в дополнительные фонды рассматривается как отток.
Притоки от этих средств рассматриваются как часть внереализационных притоков инвестиционного проекта (от операционной деятельности).
Рассмотрим задачу о возможности вложений части положительного сальдо основного инвестиционного проекта в новые инвестиционные предложения.
Допустим, задан поток финансовых поступлений и расходов на фиксированном временном интервале [t0 , T]. Обозначим его
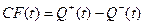 (3.4)
(3.4)
Он характеризует экзогенное (по отношению к формируемой новой инвестиционной программе) поступление средств по основному проекту на счет данной финансовой компании.
В случае, если средства базового проекта не расходуются, то, начиная с момента времени to , они могут накапливаться на счете нашей (анализируемой) фирмы в виде:
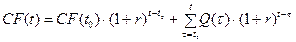 (3.5)
(3.5)
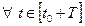
Отношение (3.5) означает, что средства, находящиеся на счете в момент времени t=t0 и обозначенные как Q(t0), растут с темпом, равным дисконту (r), а новые поступления, обозначенные через Q(τ), также пополняются с тем же темном r . При этом запись (3.5) только условно отражает фактическое развитие событий, так как предполагает, что в любой момент времени 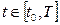 финансовые средства фирмы будут неотрицательны.
финансовые средства фирмы будут неотрицательны. 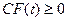 . Предполагается, все параметры базового финансового потока известны на основе какого-либо точного отображения развивающегося финансового процесса.
. Предполагается, все параметры базового финансового потока известны на основе какого-либо точного отображения развивающегося финансового процесса.
Имея финансовые средства, генерируемые базовым проектом, фирма может рассматривать множество инвестиционных предложений, которые возможно реализовывать параллельно основному проекту. Все инвестиционные предложения i =1,2,…, n можно записать с помощью следующих условий:
сроки начала новых проектов должны быть в течение жизни основного проекта;
проекты могут финансироваться за счет средств основного проекта и с привлечением долгового финансирования;
срок окончания инвестиционных предложений может не ограничивается.
Соответствующие условия записываются в виде: для каждого проекта i =1,2,…, n определяется существует или нет момент времени для которого выполняется следующее:
CFi(t)≡ CF(t), t0 ≤ t ≤toi.
CFi(t)≥0, 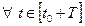 ,
,
CFi(t)= CFi(t-1)(1+r)+Q(t) +Ri(t)-Зi(t), t0i ≤ t ≤toi+Ti,
CFi(t)= CFi(t-1)(1+r)+Q(t), t0i +Ti ≤ t ≤ Ti . (3.6)
CFi(t)= CFi(t-1)(1+r)+Q(t), t0i +Ti ≤ t ≤ T
В условиях ограничений 3,6 вся совокупность проектов может быть разбита на четыре группы
Первая G1 включает те проекты, полная реализация каждого из которых возможна на временном интервале [to, Т],вторая G2 включает те проекты, реализация которых может быть начата на интервале времени [to, Т],но не закончена к моменту времени Т, т.е. t0i +Ti >T. Третью группу G3 -составляют проекты, полная реализация которых на интервале [to, Т], невозможна без дополнительного финансового обеспечения. И, наконец, четвертую группу G4 составляют номера проектов, для которых невозможна даже их частичная реализация.
Для отыскания наилучшего варианта инвестиционного предложения для первой группы инвестиционных проектов составим задачу оптимизации:
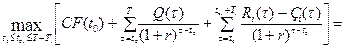 . (3.7)
. (3.7)
= 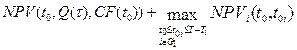 ,
,
где 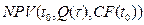 - чистая приведенная стоимость финансового потока основного проекта,
- чистая приведенная стоимость финансового потока основного проекта,
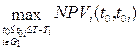 - результат выбора инвестиционного предложения с номером i* и времени начала его реализации
- результат выбора инвестиционного предложения с номером i* и времени начала его реализации 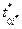 , которое обеспечивает наибольший прирост стоимости фирмы, приведенный на момент времени to без привлечения долгового финансирования в течении срока реализации инвестиционного предложения. То есть выполняется условие:
, которое обеспечивает наибольший прирост стоимости фирмы, приведенный на момент времени to без привлечения долгового финансирования в течении срока реализации инвестиционного предложения. То есть выполняется условие:
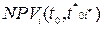 =
= 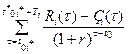 >0, i
>0, i 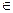 G1. (3.8)
G1. (3.8)
Для анализа возможности реализации второй группы проектов необходимо задать условие, характеризующее необходимое количество средств на счете инвестора в конечный момент времени реализации основного проекта T, т.е.:
СF(G2)( 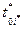 ,Q(τ), CF(t0))= CFi(T) . (3.9)
,Q(τ), CF(t0))= CFi(T) . (3.9)
Если сумма средств по основному и дополнительному проекту в период времени T больше, чем только при реализации основного проекта, то i –ый проект является эффективным (без участия долгового финансировния).
Оптимизационная задача для отыскания лучшего срока начала реализации дополнительного проекта 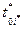 аналогична (3.7)
аналогична (3.7)
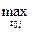 CF(G2)(
CF(G2)( 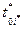 ,Q(τ), CF(t0))= CFi*(T) (3.10)
,Q(τ), CF(t0))= CFi*(T) (3.10)
В этом случае осуществляется перебор и самих проектов и сроков их начала, если сроки не фиксируются.
Третья группа проектов не может быть реализована без дополнительного долгового финансирования, т.е нарушается условие финансовой состоятельности фирмы в течение срока жизни основного проекта [to, Т], т.е .
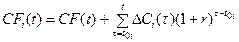 < 0 (3.11)
< 0 (3.11)
где ΔСi(t) = Ri(t)–K i(t) -3+i(t) - разность доходов и расходов
В этом случае оценка текущего состояния фирмы записывается в виде:
CFi(t + 1) = (1 + r) CFi(t) · Θ[CFi(t)] +
+ (1+d) · CFi(t) · Θ[-CFi(t)]+ ΔСi(t) +Q(t)
CFi(t0i) )=(1+r)· CFi(t0i-1) (3.12)
CFi(t)·- финансовое состояние фирмы с учетом возможных долговых обязательств в результате реализации i –го проекта;
Θ[CFi(t)] - функция Хевисайда, учитывающая наличие долгового финансирования под d % годовых, причем
Θ[Х] = 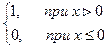 (3.13)
(3.13)
На основании текущей оценки фирмы (3.12) можно рассчитать состояние на конец периода CFi( T) в случае реализации i –го инвестиционного проекта, а также оценить возможный прирост стоимости фирмы с учетом возможного кредитования:
NPV(t0, 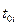 ,r,d)=
,r,d)= 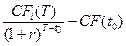 (3.14)
(3.14)
Если NPV(t0, 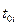 ,r,d)>0 , то реализация i –го инвестиционного проекта эффективна.
,r,d)>0 , то реализация i –го инвестиционного проекта эффективна.
Оптимизационная задача по отысканию лучшего проекта и времени его начала сводится к двум подзадачам:
по первой установим дополнительное условие о реализации нового проекта в период жизни основного, т.е. [to, Т],
NPV(t0, 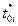 ,r,d)→max (3.15)
,r,d)→max (3.15)
по второй срок окончания нового проекта может быть позже, чем у базового, т.е t0i +Ti >T:
CFi*(T, d)→max , при t0 ≤ t0i ≤ T- Ti (3.16)
Данные оценки состояния фирмы увеличивают количество возможных инвестиционных предложений с использование не только собственных средств, но и долговых обязательств.
Таким образом, убыточное финансовое состояние фирмы, вообще говоря, может быть изменено в результате реализации эффективного инвестиционного проекта. При этом возможны следующие конкретные ситуации:
1. Реализация проекта допустима без привлечения каких-либо заемных средств и приводит к положительному сальдо наличных денег в каждый период 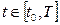
2. Реализация проекта возможна только с привлечением заемных средств и приводит к положительному сальдо наличных средств для всех 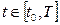
Не существует инвестиционного проекта, обеспечивающего выполнение условия положительного сальдо
