Составление графиков возврата долгосрочных кредитов
В процессе разработки инвестиционных проектов могут привлекаться кредитные ресурсы, которые возвращаются в процессе реализации проекта. Сумма кредита обычно возвращается постепенно в течение его срока. Различают два типа порядка погашения:
- периодическими взносами ("воздушный шар");
- "амортизационное" (постепенная выплата равномерными взносами).
Погашение периодическими взносами. При этом способе основную сумму кредита выплачивают на протяжении всего срока кредита. Однако порядок погашения таков, что по окончании срока от суммы кредита остается достаточно значительная доля, подлежащая погашению.
Пример 4.Представим себе, что предприятие получает кредит в сумме 100,000 р. сроком на 5 лет. Платежи в счет погашения кредита вносятся ежегодно в сумме 12,000 р. плюс процент. Таким образом, в конце 5-летнего периода, уже осуществлены четыре платежа по 12,000 р. (всего 48,000 р.), и остается невыплаченной сумма в 52,000 р., которую полностью выплачивают по окончании срока кредита. Такой порядок погашения проиллюстрирован следующей таблицей.
| Год | Начальный баланс долга | Погашение долга | Проценты | Годовая выплата | Конечный баланс долга |
| 100,000 | 12,000 | 60,000 | 72,000 | 88,000 | |
| 88,000 | 12,000 | 52,800 | 64,800 | 76,000 | |
| 76,000 | 12,000 | 45,600 | 57,600 | 64,000 | |
| 64,000 | 12,000 | 38,400 | 50,400 | 52,000 | |
| 52,000 | 52,000 | 31,200 | 83,200 | - | |
| Итог | 100,000 | 228,000 |
Заметим, что проценты начисляются исходя из величины начального на текущий год баланса долга.
Кредит может быть погашен равными взносами. Процент выплачивают по непогашенной части долга, поэтому общая сумма взноса по погашению основной суммы и процента уменьшается по мере того, как истекает срок кредита. Взносы по погашению основной суммы не изменяются. Однако каждая следующая процентная выплата меньше предыдущей, так как остающаяся непогашенной часть основной суммы уменьшается.
Если предприятие планирует погашать долг равными порциями, то график обслуживания долга будет иметь вид:
| Год | Начальный баланс долга | Погашение долга | Проценты | Годовая выплата | Конечный баланс долга |
| 100,000 | 20,000 | 60,000 | 80,000 | 80,000 | |
| 80,000 | 20,000 | 48,000 | 68,000 | 60,000 | |
| 60,000 | 20,000 | 36,000 | 56,000 | 40,000 | |
| 40,000 | 20,000 | 24,000 | 44,000 | 20,000 | |
| 20,000 | 20,000 | 12,000 | 32,000 | - | |
| Итог | 100,000 | 180,000 |
При сравнении с предыдущей таблицей приходим к выводу о том, что сумма процентных платежей в первом варианте закономерно выше.
''Амортизационное" погашение кредита. При "амортизационном" погашении основную сумму кредита выплачивают постепенно на протяжении срока кредита. Платежи осуществляют равными суммами регулярно (как правило, ежемесячно, ежеквартально или раз в полгода), и они включают определенную часть суммы кредита и процент. Вместе с последним взносом сумму кредита погашают. Этот принцип используют при ипотечном кредите. Многие западные кредитные инвесторы используют эту схему в качестве базового графика возврата долга предприятием-заемщиком.
Пример 5.Кредитный инвестор предлагает предприятию кредит под 12 процентов годовых срок на 4 года при полугодовой схеме возврата долга. Предприятие планирует привлечь 800,000 американских долларов. Необходимо рассчитать график обслуживания долга.
Прежде всего необходимо вычислить величины полугодовой выплаты. При расчете этой суммы используется концепция стоимости денег во вемени. Применительно к данному вопросу она заключается в том, что приведенная к настоящему моменту сумма всех платежей должна быть равной сумме кредита.
Если PMT - неизвестная величина годовой выплаты, а S - величина кредита, то при процентной ставке кредита і и количестве периодических платежей n величина PMT может быть вычислена с помощью уравнения:
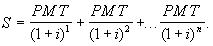
Решение этого уравнения можно произвести с помощью финансовых таблиц или электронного процессора EXCEL. Для данного примера сумма годового платежа равна 128,829. Таблица обслуживания долга имеет вид:
| Год | Начальный баланс долга | Погашение долга | Проценты | Годовая выплата | Конечный баланс долга |
| 800,000 | 80,829 | 48,000 | 128,829 | 719,171 | |
| 719,171 | 85,678 | 43,150 | 128,829 | 633,493 | |
| 633,493 | 90,819 | 38,010 | 128,829 | 542,674 | |
| 542,674 | 96,268 | 32,560 | 128,829 | 446,405 | |
| 446,405 | 102,044 | 26,784 | 128,829 | 344,361 | |
| 344,361 | 108,167 | 20,662 | 128,829 | 236,194 | |
| 236,194 | 114,657 | 14,172 | 128,829 | 121,537 | |
| 121,537 | 121,537 | 7,292 | 128,829 | ||
| Итог | 800,000 | 230,630 |
Для сравнения приведем график обслуживания той же суммы кредита по схеме погашения основной части долга равными порциями:
| Год | Начальный баланс долга | Погашение долга | Проценты | Годовая выплата | Конечный баланс долга |
| 800,000 | 100,000 | 48,000 | 148,000 | 700,000 | |
| 700,000 | 100,000 | 42,000 | 142,000 | 600,000 | |
| 600,000 | 100,000 | 36,000 | 136,000 | 500,000 | |
| 500,000 | 100,000 | 30,000 | 130,000 | 400,000 | |
| 400,000 | 100,000 | 24,000 | 124,000 | 300,000 | |
| 300,000 | 100,000 | 18,000 | 118,000 | 200,000 | |
| 200,000 | 100,000 | 12,000 | 112,000 | 100,000 | |
| 100,000 | 100,000 | 6,000 | 106,000 | - | |
| Итог | 800,000 | 216,000 |
Поскольку суммарные процентные выплаты во второй схеме существенно меньше, может показаться, что этот график более выгоден. На самом деле обе схеме одинаковы в смысле “справедливости” взаимоотношений между кредитором и заемщиком, так как современное дисконтированное значение всех годовых платежей во второй схеме, как и первой, равно исходной сумме кредита 800,000.
Задания
1.Вы заняли на четыре года $10000 под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите величину годового платежа.
2.Какие условия предоставления кредита более выгодны банку: а) 28% годовых, начисление ежеквартальное; б) 30% годовых, начисление полугодовое?
3.Предприятие приобрело здание за $20000 на следующих условиях: а) 25% стоимости оплачивается немедленно; б) оставшаяся часть погашается равными годовыми платежами в течение 10 лет с начислением 12% годовых на непогашенную часть кредита по схеме сложных процентов. Определите величину годового платежа.
4.Оцените текущую стоимость облигации номиналом $1000, купонной ставкой 9% годовых и сроком погашения через 3 года, если рыночная норма прибыли равна 7%.
5.Вычислите текущую цену бессрочной облигации, если выплачиваемый по ней годовой доход составляет 100 тыс. грн., а рыночная доходность - 12%.
6.Вы приобретаете бескупонную государственную облигацию номиналом $5000, погашаемую через 25 лет. Какова ее текущая цена, если ставка банковского процента равна 15%?
7.Вычислите текущую стоимость облигации с нулевым купоном нарицательной стоимостью 100 грн. и сроком погашения 12 лет, если приемлемая норма прибыли составляет 14%.
8.Рассчитайте текущую стоимость привилегированной акции номиналом 100 грн. и величиной дивиденда 9% годовых, если рыночная норма прибыли 12%.
9.Последний выплаченный дивиденд по акции равен $1. Ожидается, что он будет возрастать в течение следующих трех лет с темпом 14%; затем темп прироста стабилизируется на величине 5%. Какова цена акции, если рыночная норма прибыли 15%.
10.Куплена акция за $50; прогнозируемый дивиденд текущего года составит $2. Ожидается, что в следующие годы этот дивиденд будет возрастать с темпом 10%. Какова приемлемая норма прибыли, использованная инвестором при принятии решения о покупке акции?
11.Четыре года назад компания А платила дивиденд в размере $0,80 на акцию. Последний выплаченный дивиденд составил $1,66. Ожидается, что такой же среднегодовой темп прироста дивидендов сохранится и в последующие пять лет, после чего темп прироста стабилизируется на уровне 8%. Текущая рыночная цена акции $30. Следует ли покупать эту акцию, если требуемая норма прибыли составляет 18%?
12.Последний выплаченный компанией А дивиденд равен $7, темп прироста дивидендов составляет 3% в год. Какова текущая цена акций компании, если коэффициент дисконтирования равен 12%?
13.Компания А не выплачивала дивиденды в отчетном году, но в следующем году планирует выплатить дивиденд в размере $5. В последующие годы ожидается постоянный рост дивидендов с темпом 6%. Какова текущая цена акций компании, если коэффициент дисконтирования равен 13%?
14.Облигация номиналом $500 с полугодовым начислением процентов и купонной ставкой 10% годовых будет погашена через 6 лет. Какова ее текущая цена, если рыночная норма прибыли: а) 8%; б) 10%; в) 12%?
6. Оценка стоимости капитала инвестиционного проекта
