По простым процентным ставкам

Ведение

В курсе «Финансовая математика» рассматриваются различные математические расчеты, возникающие в финансовой сфере. Необходимость таких расчетов вызвана отличительной особенностью денег - деньги со временем меняют свою стоимость:

- может измениться покупательная способность денег (инфляция)

- деньги могут и должны приносить доход, если их разместить в банк под проценты или инвестировать в производство.

Таким образом, приходится рассматривать и решать две взаимообратные задачи:

наращение – определение стоимости денежной суммы в будущем, если известно значение этой суммы на данный момент времени;

дисконтирование -определение стоимости денежной суммы на данный момент времени, если известно значение этой суммы в будущем.

Решаются эти задачи путем начисления или удержания процентов.

Тема 1. Наращение и дисконтирование

по простым процентным ставкам.

1.1 Сущность процентов, период начисления, процентные ставки, наращенная сумма.

Проценты (процентные деньги) - доход от предоставления денег в долг. Измеряются проценты в денежных единицах.

Проценты начисляются периодически, т. е. каждый месяц, квартал, полугодие или год в зависимости от договора.

Период начисления – интервал времени между начислением процентов.

Сумма первоначального долга вместе с процентами за весь срок называется наращенной суммой.

Сумма процентов зависит от:

- суммы долга;

- срока долга;

- процентной ставки.

Процентная ставка - это доля дохода за период начисления от исходной суммы. Измеряется процентная ставка в процентах за период.

Виды процентных ставок:

1) ставка процентов – используется, если известна первоначальная сумма задолженности (применяется в кредитных и депозитных операциях для начисления процентов);

2) учетная ставка - используется, если известна будущая сумма задолженности, (применяется при учете векселей для нахождения дисконта).

1.2 Простые проценты.

Различают два вида ставок процентов:

1) простая ставка – каждый период проценты начисляются на одну и ту же сумму первоначального долга;

2) сложная ставка – каждый период проценты начисляются на различную накопленную сумму, т.е. на сумму первоначального долга вместе с процентами за все предыдущие периоды (проценты начисляются на проценты, капитализация процентов).

Проценты, начисляемые по простой ставке называются,простыми процентами,а по сложной ставке – сложными.

Простые проценты каждый период одинаковы, а сложные проценты возрастают с каждым периодом.

Простые проценты: Сложные проценты:

I 1 = P i I1 = P i

I 2 = P i I2 = (P+I1) i

I 3 = P i I3 = (P+I1+I2) i

…………. …,

где I _k - проценты за период k ;

P – первоначальная сумма долга;

i – ставка процентов.

Чтобы определить проценты за весь срок долга необходимо суммировать проценты за все периоды:

I = P i + P i + ….. +P i = P i n

Формула простых процентов: I=P i n ,

где I – проценты за весь срок,

n – срок долга в периодах начисления.

1.3 Точные и обыкновенные проценты.

Простые проценты, как правило, начисляются при краткосрочных операциях, когда срок долга рассчитывается в днях. В этих случаях для расчета процентов используется следующее соотношение:

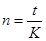, где

n - срок долга в периодах,

t - срок долга в днях,

K- временная база, т.е. количество дней за период начисления.

Срок t двумя способами:

а) точно, т. е. по календарю.

б) приближенно, когда в каждом месяце 30 дней.

И в том и в другом случае день выдачи и день погашения долга считаются за один день.

Временная база Kтак же рассчитывается двумя способами:

а) точно, когда в году 365, 366 дней.

б) приближенно, когда в году 360 дней.

Проценты называются точными, если их рассчитывают при точной временной базе и обыкновенными при приближенной.

Международные методики расчетов процентов:

1) английская – срок в днях и временная база рассчитываются точно;

2) французская – срок в днях рассчитываются точно, а временная база – приближенно;

3) германская – срок в днях и временная база рассчитываются приближенно.

1.4 Наращение по простой ставке процентов.

Наращение- это определение денежной суммы в будущем, если известно значение этой суммы на данный момент времени.

При начислении простых процентов с помощью наращения находят наращенную сумму долга, если известна первоначальная сумма.

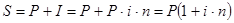
Формула наращения по простой ставке: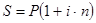

где S - наращенная сумма,

(1+ i n) - множитель наращения по простой ставке, показывает во сколько раз наращенная сумма S больше первоначальной суммы P.

Из формулы наращения можно вывести формулы для ставки и срока:

S = P (1+i n)

S =P + P i n

P i n = S - P

1) размер простой ставки процентов: i =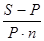

2) срок долга: n =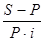

1.5 Дисконтирование по простой ставке процентов.

Дисконтирование- это определение денежной суммы на данный момент времени, если известно значение этой суммы в будущем.

При начислении простых процентов с помощью дисконтирования определяют первоначальную сумму долга, если известна его наращенная сумма, т.е. решается задача, обратная наращению.

Формула дисконтирования по простой ставке:P = ,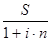

где 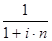- дисконтный множитель по простой ставке процентов, показывает во сколько раз первоначальная сумма долга P меньше наращенной суммы S.

Дисконтирование по простой ставке процентов называют - математическим дисконтированием.

1.6 Дисконтирование по учетной ставке.

Учетные ставки используются при учете векселей.

Учет векселя -это покупка банком векселя до срока погашения по цене ниже наминала векселя, т.е. со скидкой.

Учет векселя - это взаимовыгодная операция, т.к. клиент получает возможность обналичить вексель до его погашения, а банк, при наступлении срока погашения, получает номинал векселя и, таким образом реализует доход, равный сделанной скидке.

Доход банка при учете векселей называют дисконтом.

Сумма дисконта зависит от:

- номинала векселя;

- срока до погашения;

- учетной ставки.

Рассчитывается сумма дисконта аналогично сумме простых процентов (I=P i n)

Формула дисконта :D=S d n , где D - сумма дисконта,

S - номинал векселя,

d - учетная ставка,

n- срок до погашения.

Зная сумму дисконта, банк определяет цену векселя, путем вычисления дисконта (скидки) из номинала векселя:

P = S – D = S – S d n = S (1-d n)

Цена векселя P определяется, исходя из номинала S, который будет погашен в будущем, т.е. путем дисконтирования.

Формула дисконтирования по учетной ставке:P = S (1 - d n) ,

где P - цена векселя при учете,

(1 - d n) - дисконтный множитель по учетной ставке, который показывает во сколько раз цена векселя P меньше номинала S.

Из формулы дисконтирования выводят формулы для учетной ставки и срока:

P = S (1 - d n)

P = S - S d n

S d n = S – P

1) размер учетной ставки: d = ,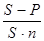

2) срок до погашения: n =