Метод оценки инвестиционного проекта по внутренней ставке дисконта

Внутренняя норма доходности (IRR) является наиболее популярным критерием эффективности инвестиций.

Под внутренней нормой доходности понимают процентную ставку в коэффициенте дисконтирования, при которой чистая современная стоимость денежного потока инвестиционного проекта NPV равна нулю.

Внутренняя норма доходности определяется путем решения следующего уравнения:

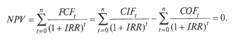
Уравнение (7.3) решается относительно IRR каким-либо итерационным методом. Нетрудно заметить, что при NPV=0 чистые приведенные стоимости поступлений и выплат проекта равны между собой. Следовательно, проект окупается.

В общем случае чем выше величина IRR, тем больше экономическая эф­фективность инвестиций. В процессе принятия решения величина IRR срав­нивается с некоторой барьерной ставкой r, отражающей требуемую инвесторами доходность либо стоимость капитала для фирмы. При этом, если IRR > r, проект обеспечивает положительную NPV и чистую доходность, рав­ную IRR - r. Если IRR < r, затраты превышают доходы и проект будет убы­точным.

• Общее правило IRR: если IRR > r, то проект принимается.________________________________

Расчет IRR ручным способом может оказаться трудоемким. Однако все со­временные программные средства инвестиционного анализа позволяют быстро и эффективно определить этот показатель. В частности, табличные процессо­ры типа MS EXCEL содержат специальные встроенные функции для его авто­матического вычисления. •

Показатель IRR, рассчитываемый в процентах, является более удобным для при­менения в анализе, чем показатель NPV, поскольку относительные величины легче поддаются интерпретации.

Критерий внутренней нормы доходности несет в себе также информацию о'при­близительной величине «предела безопасности» или риска для проекта.

Показатель IRR имеет и другие полезные интерпретации. Во-первых, он может рассматриваться в качестве максимальной ставки платы за используемые источники финансирования проекта, при которой последний остается безубы­точным.

Во-вторых, значение IRR может трактоваться как нижний уровень прибыль­ности инвестиционных затрат. Если он превышает среднюю стоимость капита­ла или норму доходности в данной отрасли, проект может быть рекомендован к осуществлению.

В-третьих, еще один вариант интерпретации состоит в трактовке внутренней нормы доходности как предельного уровня окупаемости инвестиций, что может быть критерием целесообразности дополнительных капиталовложений в проект.

Менее очевидный, но очень полезный смысл критерия заключается в том, что он показывает среднюю ставку доходности, заработанную на сумму первона­чальных инвестиций в течение срока операции. Другими словами, при условии реинвестирования денежных поступлений от проекта на оставшийся срок операции под ставку IRR их сумма будет равна будущей (наращенной) величине первона­чальных инвестиций, размещенной на тот же период под аналогичную ставку.

IRR отражает средний годовой доход по инвестиции только в тех случаях, когда проект:

- не приносит промежуточных денежных потоков;

- денежные потоки можно реинвестировать по ставке, равной самой IRR.

Критерий IRR может также приводить к некорректным выводам при анализе взаимоисключающих проектов с различными условиями реализации.

Основными причинами, обусловливающими пересечение графиков и при­водящими к противоречию критериев, являются:

. • масштаб проекта (т.е. величина первоначальных инвестиций);

• структура денежного потока.

При существовании подобных различий предприятие будет иметь неодина­ковые объемы денежных ресурсов для инвестирования и реинвестирования в зависимости от того, какой проект будет выбран. Все притоки денежных средств реинвестируются по ставке IRR, которая представляет собой среднюю взвешенную доходность за период. Таким образом, чем существеннее денеж­ные поступления на начальных этапах проекта, тем более значительной будет его IRR.

Однако конечной целью инвестирования является создание дополнитель­ной стоимости для владельцев, т.е. максимизация NPV, а не рост относитель­ной доходности. Поэтому при прочих равных условиях следует выбирать про­ект с большей NPV.

30. Деревья решений

Деревья решений обычно используются для анализа рисков проектов, име­ющих обозримое или разумное число вариантов развития. Они особо полезны в ситуациях, когда решения, принимаемые в момент времени t, сильно зависят от решений, принятых ранее, и, в свою очередь, определяют сценарии даль­нейшего развития событий.

Дерево решений имеет вид графа. Вершины графа представляют ключевые состояния, в которых возникает необходимость выбора, а дуги (ветви дерева) — различные события (решения, последствия, операции), которые могут иметь место в ситуации, определяемой вершиной. Каждой дуге (ветви) дерева могут быть приписаны числовые характеристики (нагрузки), например величина платежа и вероятность его осуществления. В общем случае использование данного метода предполагает выполнение следующих шагов.

1. Для каждого момента времени t определяют проблему и все возможные варианты дальнейших событий.

2. Откладывают на дереве соответствующую проблеме вершину и исходя­щие из нее дуги.

3. Каждой исходящей дуге приписывают ее стоимостную и вероятностную оценку.

4. Исходя из значений всех вершин и дуг рассчитывают вероятное значение критерия NPV (либо IRR, PI).

5. Проводят анализ вероятностных распределений полученных результатов.