Учет инфляционного обесценивания денег в принятии финансовых решений

Инфляция характеризуется обесцениванием национальной валюты (т.е. снижением ее покупательной способности) и общим повышением цен в стране. Очевидно, что в различных случаях влияния инфляционного процесса сказывается неодинаково. Так, если кредитор (инвестор) теряет часть дохода за счет обесценивания денежных средств, то заемщик может получить возможность погасить задолженность деньгами сниженной покупательной способности.

Во избежание ошибок и потерь в условиях снижения покупательной способности денег рассмотрим механизм влияния инфляции на результат финансовых операций и проведем несложные математические расчеты и преобразования.

Пусть Sα − сумма, покупательная способность которой с учетом инфляции равна покупательской способности суммы при отсутствии инфляции. Через ΔS обозначим разницу между этими суммами.

Отношение ΔS/S, выраженное в процентах, называется уровнем инфляции.

При расчетах используют относительную величину уровня инфляции – темп инфляции α.

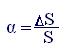
Тогда для определения Sα получаем следующее выражение:

Sα = S + ΔS = S + S α = S (1 + α). (6.1)

Величину (1+ α), показывающую, во сколько раз Sα больше S (т.е. восколько раз в среднем выросли цены), называют индексом инфляции Iи.

Iи = 1 + α.

Динамика индекса инфляции за несколько лет отражает изменения, происходящие в инфляционных процессах. Понятно, что повышение индекса инфляции за определённый период по сравнению с предыдущим таким же периодом указывает на ускорение инфляции, снижение – на уменьшение её темпов.

Пусть α – годовой уровень инфляции. Это значит, что через год сумма S ́α будет больше суммы S в (1+ α) раз. По прошествии ещё одного года сумма

S˝α будет больше суммы S ́α в (1+ α) раз, т.е. больше суммы S в (1+ α)ⁿ раз.

Отсюда видно, что инфляционный рост суммы S при годовом уровне инфляции α – то же самое, что наращение суммы S по сложной годовой ставке процентов α.

Те же рассуждения применяются, если вместо года берётся любой другой временной интервал (квартал, месяц, день и т.д.).

Очень важно запомнить, например, если каждый месяц растут цены на 2%, то за годовой уровень инфляции принимают 2% · 12 = 24%. Такие расчёты часто используют банки и финансовые компании, привлекая клиентов вкладывать средства, к примеру, под 25% годовых. Между тем, если уровень инфляции составляет 2% в месяц, это значит, что за месяц цены вырастают в (1+0,02) = 1,02 раза, а за год – в 1,02¹² = 1,268 раза. Значит, годовой темп инфляции составляет 1,268 – 1 = 0,268, т.е. годовой уровень инфляции достигает 26,8%. После такого расчета процентная ставка 25% годовых теряет свою инвестиционную привлекательность и может рассматриваться лишь в плане минимизации потерь от инфляции.

Рассмотрим теперь различные случаи задания уровня инфляции.

Если известен годовой уровень инфляции α, то за период в n лет (при том, что n = na + nb и na – целое число лет, nb – оставшаяся нецелая часть года) индекс инфляции, очевидно, составит следующую величину:

Iи = (1 + α)ⁿª (1 + nb α). (6.3)

В некоторых случаях может быть задан уровень инфляции αm за короткий (меньше года) интервал. Тогда за период, составляющий m таких интервалов, индекс инфляции будет равен

Iи = (1 + αm) . (6.4)

Теперь можно приложить изложенные в предыдущих главах варианты начисления процентов к условиям инфляционной экономики.

Если в обычном случае первоначальная сумма P при заданной ставке процентов превращается за определенный период в сумму S, то в условиях инфляции она должна превратиться в сумму Sα, используем формулу (1.7):

Sα = P (1 + iα).

Для данной суммы можно записать еще одно соотношение:

Sα = P (1 + i) (1 + α),

а затем составить уравнение эквивалентности:

(1 + iα) = (1 + i) (1 + α),

из которого следует, что

iα = i + α + I α. (6.5)

Мы получили, таким образом, формулу И.Фишера, в которой сумма (α + i α) является величиной, которую необходимо прибавить к реальной ставке доходности для компенсации инфляционных потерь. Эта величина называется инфляционной премией.

Знаяформулу И.Фишера, можно избежать еще одной распространенной ошибки. Часто для подсчета процентной ставки, учитывающей инфляцию, к величине реальной ставки доходности просто прибавляют величину темпа инфляции, т.е. если i = 25% и α = 15%, то за процентную ставку, учитывающую инфляцию, принимается сумма (i + α) = 25 + 15 = 40%. Но нужно помнить, что существует еще произведение (i α), величина которого тем больше, чем больше значения i и α. В нашем примере оно составляет 0,15 · 0,25 = 0,0375 = 3,75%. Наверное не стоит, пренебрегать даже такой, на первый взгляд, небольшой величиной. Ведь когда счет идет на десятки миллионов, каждый процентный пункт — это сотни тысяч рублей.

Рассмотрим теперь различные случаи начисления |процентов с учетом инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период.

Для простых процентных ставок по формуле (1.7) получаем

Sα = P (1 + n iα).

В то же время должно выполняться равенство:

Sα = P (1 + n i) Iи.

Составим уравнение эквивалентности:

1 + n iα = (1 + n i) Iи.

из которого получаем

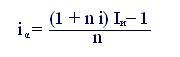
(6.6)

Для простых учетных ставок аналогичное уравнение эквивалентности будет иметь вид:

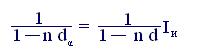
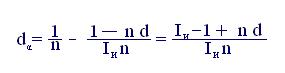
(6.7)

Для случая сложных процентов используем формулу (3.1):

Sα = (1 + icα)ⁿ;

Sα = (1 + ic)ⁿ lи.

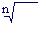Отсюда

icα = (1 + ic) Iи – 1. (6.8)

Если начисление процентов происходит несколько (m) раз году, используем формулу (3.6):

(1 + jα/m) = (1 + j/m) Iи.

Отсюда

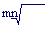jα = m [(1 + j/m) Iи – 1].

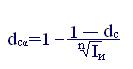Таким же образом получаем две формулы для случая сложных учетных ставок:

(6.10)

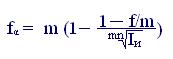
(6.11)

Используя полученные формулы, можно находить процентную ставку, компенсирующую потери от инфляции, когда заданы процентная ставка, обеспечивающая желаемую доходность финансовой операции, и уровень инфляции в течении рассматриваемого периода.

Эти формулы можно преобразовать и получить зависимость

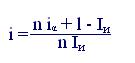i от iα или любую другую. Например, из формулы (6.6) можно получить формулу, позволяющую определит реальную доходность финансовой операции, когда задан уровень инфляции и простая ставка процентов, учитывающая инфляцию:

(6.12)

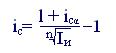Из формулы (6.8) получаем аналогичную формулу для случая сложных процентов:

(6.13)

Подставив в последнюю формулу вместо индекса инфляции выражение (1 + α)ⁿ, получим простую формулу:

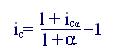
(6.14)

отражающую несколько очевидных соображений:

если icα = α (доходность вложений и уровень инфляции равны), то

ic = 0, т.е. весь доход поглощается инфляцией;

если icα < α (доходность вложений ниже уровня инфляции), то ic < 0, т.е. операция приносит убыток;

если icα > α (доходность вложений выше уровня инфляции), то ic > 0, т.е. происходит реальный прирост вложенного капитала.

ПРИМЕР 20

Первоначальный капитал в размере 20 000 000 руб. выдан на два года. Реальная доходность операций должна составить 10% годовых по сложной ставке ссудного процента. Ожидаемый уровень инфляции составляет 15% в год. Определить множитель наращения, сложную ставку процентов, учитывающую инфляцию, и наращенную сумму.

Решение

По формуле (6.3) получаем

Iи = (1 + 0,15)² = 1,3225.

Множитель наращения и номинальная ставка доходности равны:

kн.c = (1 + 0,1)² = 1,3225.

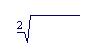icα = (1 + 0,1) 1,3225 – 1 = 0,265 = 26,5%.

Далее для наращенной суммы получаем

S = 50 000 000 (1 + 0,265)² = 80 011 250 (руб.)

ПРИМЕР 21

Первоначальный капитал в размере 20 000 000 руб. выдается на три года, проценты начисляются в конце каждого квартала по номинальной ставке 8% годовых. Определить номинальную ставку процентов и наращенную сумму с учетом инфляции, если ожидаемый годовой уровень инфляции составляет 12%.

Решение

Воспользуемся формулой (6.3):

Iи = (1 + 0,12)³ = 1,4

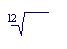По формуле (6.9) имеем

jα = [(1 + 0,08/4) 1,4 – 1] 4 = 0,107 = 10,7%.

Отсюда

S = 20 000 000 (1 + 0,107/4)¹² = 27 454 048 (руб.).

ПРИМЕР 22

При выдаче кредита должна быть обеспечена реальная доходность операции, определяемая учетной ставкой 5% годовых. Кредит выдается на полгода, за которые предполагаемый индекс инфляции составит 1,06. Рассчитать значение учетной ставки, компенсирующей потери от инфляции.

Решение

Производим вычисления по формуле (6.7):

dα = (1,06 – 1 + 0,5 · 0,05)/( 1,06·0,5) = 0,16 = 16%.

ПРИМЕР 23

Определить реальную доходность финансовой операции, если при уровне инфляции 0,9% в месяц выдается кредит на два года по номинальной ставке сложных процентов:

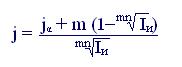
(6.15)

По формуле (6.4):

Iи = (1 + 0,009) = (1,009³) = 1,027 .

Отсюда

j = [0,15 + 4(1 – 1,027)]/1,027 = 0,038 = 3,8%.

ПРИМЕР 24

Определить, какой реальной убыточностью обладает финансовая операция, если при уровне инфляции 14% в год капитал вкладывается на один год под номинальную ставку 8% при ежемесячном начислении.

Решение

Находим сначала индекс инфляции:

Iи = 1 + 0,14 = 1,14.

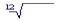
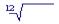Далее используем формулу (6.15):

j = [0,08 + 12(1 − 1,14)]/ 1,14 = -0,051 = -5,1%.

Таким образом, данная операция будет приносить 5,1%-ный убыток.

АННУИТЕТЫ

В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или, наоборот, выплат) в течение определенного периода. Это может быть серия доходов и расходов некоторого предприятия, выплата задолженностей, регулярные или нерегулярные взносы для создания разного рода фондов и т.д. Такая последовательность называется потоком платежей.

Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом (финансовой рентой).

Теория аннуитетов является важнейшей частью финансовой математики. Она применяется при рассмотрении вопросов доходности ценных бумаг, в инвестиционном анализе и т.д. Наиболее распространенные примеры аннуитета: регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам.

Аннуитеты различаются между собой следующими основными характеристиками:

• величиной каждого отдельного платежа;

• интервал времени между двумя последовательными платежами (периодом аннуитета);

• сроком от начала аннуитета до конца его последнего периода (бывают и неограниченные по времени − вечные аннуитеты);

• процентной ставкой, применяемой при наращении или дисконтировании платежей.

Аннуитеты, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренумерандо; если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо(обыкновенный аннуитет) – пожалуй, самый распространенный случай.

Наибольший интерес с практической точки зрения представляет аннуитеты, в которых все платежи равны между собой (постоянные аннуитеты), либо изменяются в соответствии с некоторой закономерностью. Именно такие аннуитеты мы и изучим в дальнейшем.

Введем следующие обозначения:

P – величина каждого отдельного платежа;

ic – сложная процентная ставка, по которой начисляются проценты;

Sk – наращенная сумма для k-го платежа аннуитета постнумерандо;

S – наращенная (будущая) сумма всего аннуитета постнумерандо (т.е. сумма платежей с процентами);

Ak – современная величина k-го платежа аннуитета постнумерандо;

А – современная величина всего аннуитета постнумерандо (т.е. сумма современных величин всех платежей);

Sп – наращенная сумма аннуитета пренумерандо;

Ап – современная величина аннуитета пренумерандо;

n – число платежей.

Рассмотрим аннуитет постнумерандо с ежегодным платежами Р в течение n лет, на которые начисляются проценты по сложной годовой ставке iс (см. приложение, рис. 5).

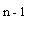Сумма S1 для первого платежа, проценты на который будут начисляться, очевидно, (n – 1) раз, составит по формуле (3.1):

S1 = P(1 + ic) .

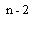Для второго платежа (проценты на него будут начисляться на один год меньше) имеем

S2 = P(1 + ic)

и так далее. На последний платеж, произведенный в конце n-го года, проценты уже не начисляются, т.е.

Sn = P.

Тогда для общей наращенной суммы имеем

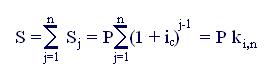
(7.1)

где ki,n – коэффициент наращения аннуитета с параметрами i, n – представляет собой, как можно заметить, сумму членов геометрической прогрессии, для которой первый член a1 равен 1, а знаменатель (назовем его q) составляет (1 + ic).

Используя математическую формулу для суммы геометрической прогрессии:

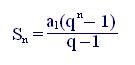
запишем

выражение (7.1) в более удобном для вычисления виде:

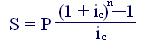
(7.2)

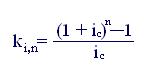Для коэффициента наращения, соответственно, имеем

(7.3)

Найдем теперь современную величину А данного аннуитета (см. приложение, рис. 6).

При заданной процентной ставке ic современное значение каждого платежа будет определяться по формуле:

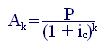
Современная величина всего аннуитета, следовательно, составит

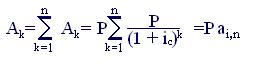
где аi,n – коэффициент приведения аннуитетов, опять является суммой геометрической прогрессии, теперь уже с параметрами a1 = q =1/(1 + ic).

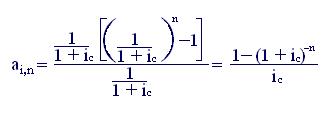Тогда для аi,n получаем выражение:

(7.4)

для современной величины А соответственно

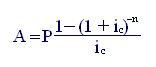
(7.5)

Как видим, современная величина и наращенная сумма аннуитета связаны между собой соотношением:

S = A (1 + ic)ⁿ. (7.6)

Из полученных формул путем преобразований легко получить еще несколько формул.

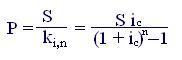Так, для определения размера очередного платежа (Р) имеем

(7.7)

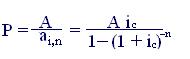
(7.8)

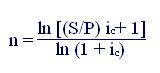Для определения срока аннуитета (n) при прочих заданных условиях, получаем

; (7.9)

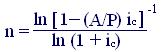
(7.10)

Для конкретных вычислений выбирается одна из двух формул каждой пары в зависимости от заданных известных величин.

Рассмотрим далее аннуитет пренумерандо с теми же начальными условиями (см. приложение, рис. 7).

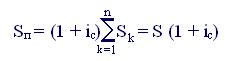Отличие от предыдущего случая состоит здесь в том , что период начисления процентов на каждый платеж увеличивается на один год, т.е. каждая наращенная сумма Sk увеличивается в (1 + ic) раз. Следовательно, для всей суммы Sп имеем

(7.11)

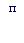
Для коэффициента наращения аннуитета пренумерандо ki,n получаем следующее соотношение:

ki,n = ki,n ·(1 + ic). (7.12)

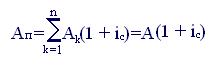Можно также заметить, что для определения современных значений каждого платежа дисконтирование по заданной ставке ic проводится на один раз меньше, чем в случае аннуитета пренумерандо. Поэтому каждая современная величина Аk будет больше в (1 + i) раз. Таким образом,

(7.13)

Для коэффициента приведения а i,n получаем

а i,n = аi,n(1 + ic). (7.14)

Для нахождения размера платежа и срока аннуитета пренумерандо можно по формулам (7.11) и (7.13) найти для значений Sп и Ап соответствующие значения S и А и пользоваться далее формулами, выведенными для аннуитета постнумерандо.

Для определения коэффициентов наращения и приведения обыкновенного аннуитета существуют таблицы, которыми удобно пользоваться в практических вычислениях. Максимальные процентные ставки в таких таблицах обычно не превышают 30−40%, что значительно ниже размера процентных ставок, применяемых в России в настоящее время. Но нужно иметь в виду, что n в данном случае – не число лет, а число периодов одинаковой продолжительности (день, месяц, квартал и т.д.), в которых принята данная процентная ставка. Таким образом, если задана годовая процентная ставка, можно найти эквивалентную ей ставку на более коротком интервале и рассматривать далее n как число таких интервалов.

Если срок аннуитета n не ограничен, мы получаем случай вечного аннуитета. Для аннуитета постнумерандо выражения для наращенной суммы и современной величины приобретут следующий вид:

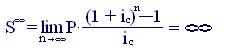
(7.15)

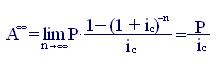
(7.16)

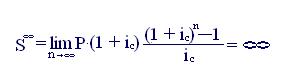Для аннуитета пренумерандо, соответственно, получаем

(7.17)

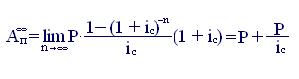
(7.18)

Таким образом, различие между типами вечных аннуитетов, естественно, сказывается на определении их современной величины.

Не менее важен случай, когда последовательность платежей изменяется по некоторому закону, и, следовательно, также может быть описана с помощью математических средств.

Рассмотрим обыкновенный аннуитет, в котором платежи постоянно увеличиваются на определенную положительную величину h, т.е. являются арифметической прогрессии с первым членом а1 = Р и разностью h. Т. с. Платежи представляют собой ряд:

Р, Р + h, P + 2h, . . . P + (n – 1)h.

Для наращенной суммы всего аннуитета получаем следующее выражение:

S = P(1 + ic) + (P + h)(1 + ic) + (P +2h)(1 + ic) + … + [P + (n −1)h].

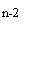Умножим обе части данного равенства на (1 + ic) и вычтем первое выражение из полученного после умножения:

S·ic = P(1 + ic)ⁿ − [P + (n – 1)h] + h(1 + ic) + h(1 + ic) + … + h(1 + ic).

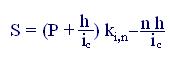Видно, что часть полученного равенства представляет собой сумму членов геометрической прогрессии, где а1 = h(1 + ic); q = (1+ ic). После несложных преобразований получаем:

(7.19)

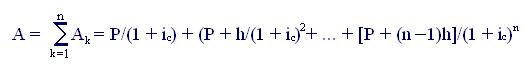Найдем теперь современное значение аннуитета А.

(7.20)

Умножим обе части равенства на (1 + ic)ⁿ.

A(1 + ic)ⁿ = P(1 + ic) + (P + h)(1 + ic) + … + [P + (n – 1)h] = S.

Как видим, в данном случае верна формула (7.6). полученная ранее для обыкновенного аннуитета:

А (1 + ic)ⁿ = S,

отсюда

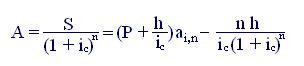
(7.20)

Возможен также случай, когда платежи постоянно возрастают в q раз, т.е. являются членами геометрической прогрессии:

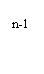P, Pq, Pq², …, Pq .

Тогда для наращенной суммы аннуитета имеем

S = P[(1 + ic) + q(1 + ic) +q²(1 + ic) + … +q ].

В квадратных скобках мы получили геометрическую прогрессию с первым членом а1 = (1 + ic)ⁿ и знаменателем q/(1 + ic). Используя опять формулу для суммы геометрической прогрессии, получаем выражение для S:

S = P [qⁿ – (1 + ic)ⁿ]/[q – (1 + ic)].

Очевидно, чтобы найти современное значение аннуитета А, здесь также можно применить формулу (7.6):

A = P[qⁿ/(1 + ic)ⁿ – 1]/[q – (1 + ic)].

Теперь мы имеем возможность решить пример по определению потока платежей произвольной величины.

ПРИМЕР 25

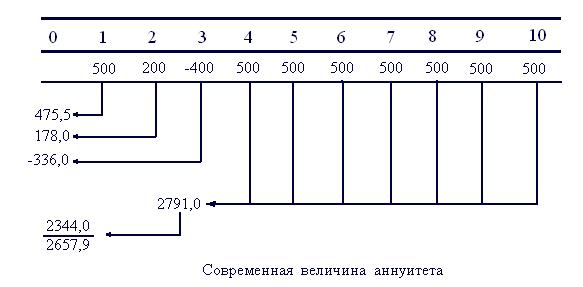
Найти современную величину потока платежей, определяемого следующим образом: первый год – поступления 500 ам. долл., второй год – поступления 200 ам. долл., третий год – выплата 400 ам. долл., далее в течение семи лет – доход по 500 ам. долл. Ставка дисконтирования – 6% годовых.

Решение

В данном примере поток платежей в течение последних семи лет представляет собой постоянный аннуитет. По форме (7.5) мы можем рассчитать его современную величину А0. Нельзя забывать, что это будет современная величина на момент начала четвертого периода:

А0 = 500 · 5,58 = 2791 (ам. долл.)

Далее, используя формулу (3.11), находим современные значения на момент начала потока платежа для всех оставшихся платежей и величины А0:

А1 = 500 · 0,953 = 471,5 (ам. долл.);

А2 = 200 · 0,89 = 178 (ам. долл.);

А3 = -400 · 0,840 = -336 (ам. долл.);

А4 = 2791 · 0,840 = 2344,44 (ам. долл.).

Складывая получившиеся величины, находим современную величину всего потока платежей:

А = А1 + А2 + А3 + А4 = 2657,94 ам. долл.

Во всех случаях, когда в произвольном потоке платежей встречаются серии, которые могут быть описаны как постоянные или изменяющиеся по некоторому закону аннуитеты, следует обращать внимание на начальный момент и срок этих аннуитетов, не совпадающие с начальным моментом и сроком полного потока платежей.

Следующий этап нашего изучения – конверсия аннуитетов.

Под конверсией аннуитетов понимается такое изменение начальных параметров аннуитета, после которого новый аннуитет был бы эквивалентен данному.

Два аннуитета считаются эквивалентными, если равны их современные величины, приведенные к одному и тому же моменту времени.

На практике необходимость рассчитать параметры эквивалентного аннуитета чаще всего возникает при изменении условий выплаты долга, погашения кредита или займа и т.п. При этом конверсия может произойти как в момент начала аннуитета (на этот момент и рассчитываются современные величины эквивалентных аннуитетов), так и после выплаты некоторой части аннуитета. В последнем случае все расчеты производятся на остаток долга в момент конверсии.

Рассмотрим наиболее распространенные случаи конверсии постоянных аннуитетов.

1. Через некоторый промежуток времени n0 (он может быть равен и 0) после начала аннуитета весь остаток долга может быть выплачен за один раз (выкуп аннуитета). Очевидно, что в этом случае величина выплачиваемой суммы будет равна современной величине остатка аннуитета, рассчитанной для срока n1 = n – n0.

2. Может возникнуть задача, обратная предыдущей: задолженность погашается частями, в виде выплаты постоянного аннуитета, и требуется определить один из параметров аннуитета при заданных остальных. Поскольку здесь известна сумма долга, т.е. современная величина аннуитета, для нахождения неизвестного параметра используем формулы (7.8) или (7.10).

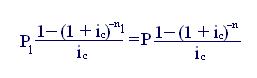3. Период выплаты долга может быть изменен при сохранении прежней процентной ставки. Величину Р1 платежа для срока n1 находим, используя уравнения эквивалентности (приравниваются современные значения аннуитетов):

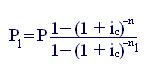
Отсюда

.

Очевидно, что, если срок аннуитета увеличится, значение Р сохранится, и наоборот.

4. Может возникнуть ситуация, когда величина платежа Р должна быть изменена в ту или другую сторону. Рассмотрим данный случай на примере 26.

ПРИМЕР 26

Для погашения кредита, выданного под сложную процентную ставку 4% годовых, в течение 10 лет должны вноситься ежегодные платежи в размере 5 000 ам. долл. Изменившиеся условия дают возможность с самого начала вносить по 7 500 ам. долл. Определить новый срок n1. за который долг будет полностью выплачен.

Решение

Рассчитаем сначала современную величину имеющегося аннуитета (которая и представляет собой величину долга на начальный период).

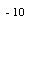По формуле (7.5) получаем

А = 5 000 [1 – (1 + 0,04) ]/0,04 = 40554,5 (ам. долл.).

Далее для изменившегося Р найдем коэффициент приведения аннуитета по той же формуле:

аi,n = A/P1 = 40554,5 ам. долл./ 7500 ам. долл. = 5,4.

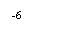Значение n, более всего подходящее данному коэффициенту при процентной ставке 4%, это n1 = 6(приближенно). Поскольку значение n1 найдено приближенно, необходимо рассчитать современное значение нового аннуитета:

А1 = 7 500 [1 – (1 + 0,04) ]/0,04 = 39 316 (ам. долл.).

Если величины платежей изменяться не могут, недостающая сумма А0 = 40 554,5 – 39 316 = 1238,5 (ам. долл.) должна быть выплачена кредитору сразу.

5. Начало выплаты задолженности при заданной процентной ставке ic может быть отсрочено:

а) при сохранении размера платежа;

б) при сохранении срока выплаты.

Очевидно, что в первом случае должен увеличиться срок аннуитета, а во втором – величина платежа.

Обозначим через n0 период отсрочки. Тогда на момент начала выплаты, сумма долга А1, которая должна являться современной величиной нового аннуитета, составит по формуле сложного процента:

А1 = а(1 + ic) .

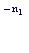Отсюда получаем уравнение эквивалентности:

P1[1 – (1 + ic) ] = P[1 – (1 + ic) ] · (1 + ic)

Далее поступаем аналогично рассмотренным ранее случаям. В первом варианте находим значение n1 продолжительности нового аннуитета при заданном значении Р1 = Р(n1 будет найдено приближенно, поэтому потребуется выплата компенсирующей суммы, см. пример 26). Во втором – величину платежа Р1 при n1 = n – n0.

6. В некоторых случаях может потребоваться объединение нескольких аннуитетов в один (консолидация аннуитетов). При этом объединяемые аннуитеты могут быть любыми, а в искомом объединяющем аннуитете один из параметров неизвестен при всех остальных заданных.

ПРИМЕР 27

Два аннуитета с параметрами:

1) величина платежа – 2 000 ам. долл., процентная ставка – 5% годовых, срок – 12 лет;

2) величина платежа – 3 500 ам. долл., процентная ставка – 6% годовых, срок – 10 лет;

требуется заменить одним – со сроком 10 лет и процентной ставкой 6% годовых.

Определить величину нового платежа.

Решение

Найдем сначала общую современную величину двух аннуитетов. По формуле (7.5) имеем

A = A1 + A2 = 2 000[1 – (1 + 0,05) ]/0,05 +

+ 3 500 [1 – (1 + 0,06) ]/0,06 = 17 726,5 + 25 760,3 = 43 486,8 (ам. долл.)

Далее по формуле (7.7) находим величину нового платежа:

Р = 43 486,8 · 0,06/[1 – (1 + 0,06) ] = 5 930 (ам. долл.)

Нам остается теперь рассмотреть важное практическое приложение теории аннуитетов – составление различных вариантов (планов) погашения задолженности. При составлении плана погашения интерес представляют размеры периодических платежей заемщика – выплаты процентов и выплаты по погашению основанной суммы долга – при различных условиях погашения (такие платежи носят название срочных уплат).

Основных вариантов погашения задолженности – четыре:

1. Займы без обязательного погашения, по которым постоянно выплачиваются проценты. Задача в данном случае заключается в нахождении размера выплачиваемой суммы Р при заданной процентной ставке i. Мы имеем здесь случай вечного аннуитета. Размер платежа определяется по формуле (7.15), из которой получаем

P =Aic

2. Погашение долга в один срок.

Если заемщик должен вернуть всю сумму долга в конце срока, целесообразным бывает создание погасительного (амортизационного) фонда, для чего периодически вносятся определенные суммы, на которые начисляются проценты.

Если процентная ставка, под которую вносятся средства, не превышает размера ставки, под которую выдается заем, создание погасительного фонда не имеет смысла. Выгоднее сразу расплачиваться этими суммами с кредитором.

Введем обозначения:

D – основная сумма долга (без процентов);

ic – ставка процентов по займу;

I – процент по займу;

P – размер взноса в погасительный фонд;

g – ставка, по которой начисляются проценты на взносы в фонд;

Y – величина срочной уплаты;

N – срок займа.

Найдем величину срочной уплаты Y и ее составляющих (Y = I + P).

По определению I = D ic.

Сумма, накопленная в погасительном фонде за n лет, т.е. наращенная сумма аннуитета с параметрами P, n, g, должна составить величину D. По формуле (7.2) получаем

D = P[(1 + g)ⁿ – 1]/g.

Отсюда

P = D g /[(1 + g)ⁿ – 1].

Значит, в данном случае величина срочной уплаты определяется формулой:

Y = D ic + D g / [(1 + g)ⁿ – 1].

Если проценты не выплачиваются, а присоединяются к основной сумме долга, то срочная уплата будет состоять из взносов в погасительный фонд.

Общая сумма долга составит по формуле (3.1) величину D (1 + ic)ⁿ, откуда получаем

Y = P = D (1 + ic)ⁿ g / [(1 + g)ⁿ – 1].

3. Погашение долга равными суммами

Пусть долг погашается в течение n лет равными суммами, а проценты периодически выплачиваются. Тогда на погашение постоянно идут платежи размером D/n, а процентные выплаты ежегодно сокращаются, так как уменьшается основная сумма долга.

Обозначим

Dk – сумма долга после k-го года:

Ik – процентная выплата за k-й год.

Тогда

D1 = D – D/n = D (1 – 1/n);

I1 = D ic;

Y1 = D ic + D/n

На конец второго года получаем

D2 = D1 – D/n = D (1 – 2/n);

I2 = D (1 – 1/n)ic;

Y2 = D (1 – 1/n)ic + D/n, и т.д.

Для определения размера срочной уплаты и процентного платежа после k-го года получаем

Dk = D (1 – k/n);

Ik = D [1 – (k – 1)/n] ic;

Yk = D [1 – (k – 1)/n] ic + D/n.

На конец срока, т.е. n-го года имеем

Dn = D (1 – n/n) = 0;

Yn = D [1 – (n – 1)/n] ic +D/n = D (1 + ic)/n.

Видно, что самые большие суммы приходится платить в начале периода погашения, что может в большинстве случаев расцениваться как недостаток этого метода погашения задолженности.

4. Погашение долга с использованием постоянных срочных уплат

Пусть займ величиной D, выданный под сложную годовую процентную ставку ic, погашается в течение n лет равными срочными уплатами Y = I + P. Понятно, что со временем составляющая I (проценты по займу) будет уменьшаться, так как уменьшается основная сумма задолженности. Соответственно, составляющая Р (сумма, идущая на погашение займы) будет увеличивается.

Выведем формулу для расчета суммы процентных денег и суммы на погашение долга на конец k-го года.

Периодическая выплата постоянной суммы Y при заданной процентной ставке ic в течение n лет является аннуитетом с соответствующими параметрами.

Поэтому величина срочной уплаты определяется по формуле (7.9):

Y = D/ai,n (ai,n - коэффициент приведения ренты).

Обозначим через Рk сумму, идущую на погашение займа в конце –го года, запишем следующие соотношения:

1) Ik + Pk = Ik+1 + Pk+1;

2) Dk = Dk-1 – Pk;

3) Ik = Dk-1 ic, откуда Dk-1 = Ik/ic;

4) Ik+1= Dkic, откуда Dk = I k+1/ic.

Произведя различные преобразования получаем

Ik = D k-1 ic = Dic – D(1/ai,n – ic)[(1 + ic) −1].

Когда займ погашается постоянными срочными уплатами, их величина может быть заранее задана, и тогда возникает задача определения периода погашения долга n. Вопрос определения срока аннуитета рассматривался ранее в связи с конверсией аннуитетов. При этом для выполнения принципа эквивалентности необходимо было доплатить недостающую сумму (возникающую в результате округления полученного n) в начале периода погашения. Вместо этого возможно также небольшое изменение размера срочных уплат.

Рассмотрим для прояснения ситуации пример.

ПРИМЕР 28

Займ в размере 12 000 ам. долл. выдан под сложную процентную ставку 4% годовых. Определить продолжительность периода погашения, если заемщик собирается выплачивать ежегодно по 1 500 ам. долл. Составить график погашения долга.0

Решение

Рассчитаем сначала коэффициент приведения аннуитета а4,n:

а4,n = A/P = 12 000 ам. долл. / 1 500 ам. долл. = 8.

По таблице определим приблизительно n, соответствующее данному коэффициенту и процентной ставке 4%. Так как n=10 соответствует коэффициент а4,10 = 8,11, возьмем n=9 и рассчитаем для этого срока и современной величины А=12 000 ам. долл. новое значение платежа Р. Используем для этого формулу (7.8):

P =A/a4,9 = 12 000 ам. долл..7,435 = 1 614 ам. долл.

Составим теперь график погашения долга, в который должны входить процентные выплаты, расходы по погашению долга, остаток долга на конец каждого года.

Используя выведенные ранее формулы, находим искомые значения:

Год	Сумма долга на конец года	Срочная уплата (Y)	Проценты (I)	Выплата на Погашение (Р)
	10 866,0 9 686,67 8 460,2 7 184,6 5 858,0 4 478,32 3 043,5 1 551,23	1613,99 1613,99 1613,99 1613,99 1613,99 1613,99 1613,99 1613,99 1613,99	480,0 434,64 387,47 338,4 287,4 234,32 179,13 121,73 62,04	1133.98 1179,35 1226,5 1275,58 1326,6 1379,67 1434,86 1492,25 1551,9