Дисконтирование по сложной ставке
1. Математическое дисконтирование –обратная задача наращению.
,
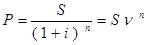где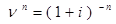 
- дисконтный множитель;
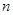- срок от момента учета до даты погашения векселя;
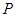- современная стоимость 
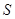, которая может быть рассчитана на любой момент до выплаты суммы .
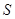При этом величина дисконта
.
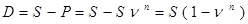При дисконтировании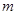 
раз в году
.
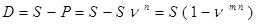Операции со сложной учетной ставкой.
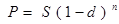, (6)
где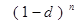 
- дисконтный множитель.
Дисконтирование 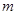раз в году проводится c на базе номинальной учетной ставки 
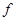, каждый раз по ставке 
:
.
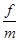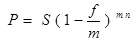Эффективная учетная ставкахарактеризует результат дисконтирования за год и определяется из равенства:
.
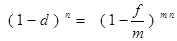
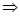
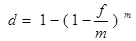Номинальная ставка через эффективную:
.
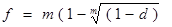Определение периода начисления и величины
процентной ставки для сложных процентов
Для вычислений используем формулы (5), (6).
· по ставке процентов:
; 
.
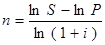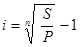· по учетной ставке:
; 
.
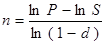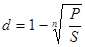Непрерывные проценты
Непрерывное наращение
Непрерывное наращение – это наращение за бесконечно малые отрезки времени. Используется в анализе сложных финансовых проблем – при проектировании, выборе инвестиционных решений и т.д.
Способ расчета наращенной суммы зависит от вида процентной
ставки:
· вид ставки – постоянная сила роста:
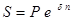, (7)
где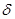 
- сила роста, т.е. номинальная ставка процентов при 
,
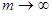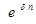- множитель наращения.
Дискретные и непрерывные ставки функционально зависят:
.
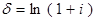· вид ставки – переменная сила роста:
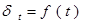- непрерывная функция времени.
Тогда наращенная сумма
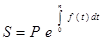. (8)
Если сила роста изменяется по линейному закону, то
,
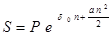где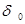 
- начальное значение силы роста (при 
),
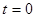а - годовой прирост.
Дисконтирование на основе непрерывных процентных ставок
Математическое дисконтирование.
Современная стоимость определяется из формул (7), (8):
,
,
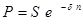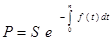где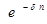 
, 
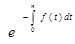- дисконтные множители.
Банковский учет.
,
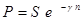где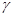 
- сила дисконта т.е. номинальная учетная ставка при ,
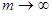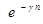- дисконтный множитель.
Финансовые ренты
Финансовая рента (аннуитет) –это регулярный поток финансовых платежей, все члены которого положительны, а временные интервалы между платежами равные. К финансовым рентам относятся платежи по потребительскому кредиту, выплаты страховых премий, процентов по облигациям и т.д.
Основные параметры финансовой ренты:
Член ренты – размер отдельного платежа;
Срок ренты– время от начала ренты до ее конца;
Период ренты– временной интервал между двумя последовательными платежами;
Процентная ставка.
Наращенная сумма – сумма всех членов потока платежей с начисленными на них к концу срока процентами.
Современная стоимость потока платежей –сумма всех его членов, дисконтированных на начало срока ренты или на предыдущий момент времени.