Задача для самостоятельного решения № 1
Проект генерирует следующие денежные потоки по годам:
С0 , С1, С2, С3, С4, С5.
Ставка дисконтирования равна E %.
Оцените целесообразность участия в проекте, рассчитав следующие показатели:
- чистый дисконтированный доход проекта (NPV);
- дисконтированный срок окупаемости (DPBP);
- внутренняя норма прибыльности (IRR);
- индекс рентабельности (PI);
- модифицированная внутренняя норма прибыльности (МIRR).
Замечание. Для расчёта IRR и DPBP первые Nотриц денежных потоков возьмите со знаком «минус», остальные со знаком «плюс», вне зависимости от их знаков в таблице.
| № варианта | С0 | С1 | С2 | С3 | С4 | С5 | E | Nотриц |
| -3020 | ||||||||
| -2360 | -1895 | |||||||
| -7740 | -1911 | -202 | ||||||
| -6980 | -2068 | |||||||
| -7360 | ||||||||
| -8840 | -1128 | -3340 | ||||||
| -2290 | -2436 | -7784 | ||||||
| -8580 | -3072 | |||||||
| -3180 | -3660 | -992 | ||||||
| -10620 | -676 | |||||||
| -3440 | -335 | -139 | -611 | |||||
| -2600 | -2835 | -931 | -2847 | |||||
| -6430 | -2240 | -3870 | ||||||
| -7660 | -5240 | |||||||
| -5840 | -2631 | -3760 | ||||||
| -8140 | -510 | -309 | -4722 | |||||
| -10120 | -2208 | |||||||
| -5120 | -684 | -4734 | ||||||
| -7530 | -1386 | -2604 | ||||||
| -2160 | -27 | |||||||
| -9940 | -54 | -2208 | ||||||
| -6440 | -917 | |||||||
| -9330 | -165 | -4670 | -2060 | |||||
| -10760 | ||||||||
| -8790 | -6291 | |||||||
| -3990 | -1722 | |||||||
| -8920 | -936 | |||||||
| -8750 | -5117 | -1786 | ||||||
| -6190 | -948 | -831 | ||||||
| -2280 |
Самостоятельная работа № 2. Пространственная оптимизация распределения инвестиций по нескольким проектам.
4.1. Пространственная оптимизация: проекты поддаются дроблению.
Имеется в виду, что можно реализовывать не только целиком каждый из анализируемых проектов, но любую его часть; при этом берется к рассмотрению соответствующая доля инвестиций и денежных поступлений. Последовательность действий в этом случае такова:
1) для каждого проекта рассчитывается индекс рентабельности;
2) проекты упорядочиваются по убыванию показателя PI;
3) в инвестиционную программу включаются первые k проектов, которые в сумме в полном объеме могут быть профинансированы предприятием;
4) очередной проект берется не в полном объеме, а лишь в той части, в которой он может быть профинансирован (остаточный принцип).
Пример 7.
Предположим, что предприятие имеет возможность инвестировать до 55млн. рублей, при этом цена источников финансирования составляет 10 %. Требуется составить оптимальную инвестиционную программу, если имеются следующие альтернативные проекты (млн. руб.):
1) проект А: - 30; 6; 11; 13; 12;
2) проект Б: - 20; 4; 8; 12; 5;
3) проект В: - 40; 12; 15; 15; 15;
4) проект Г: -15; 4; 5; 6;
Решение:
• Рассчитаем чистый приведенный эффект (NPV) и индекс рентабельности для каждого проекта (PI):
• проект А: NPV = 2,51; PI = 1.084; IRR = 13.4%;
• проект Б: NPV = 2,68; PI = 1.134; IRR = 15.6%;
• проект В: NPV = 4,82; PI = 1.121; IRR = 15.3%;
• проект Г: NPV = 1,37; PI = 1.091; IRR = 13.9%;
• По убыванию показателя PI проекты упорядочиваются следующим образом: Б,В,Г,А.
• Наиболее оптимальной будет стратегия:
| Проект | Инвестиция | Часть инвестиции, включаемая в портфель, % | NPV |
| Б | 100,0 | 2,68 | |
| В | 87,5 | 4,22 | |
| Всего | 6,90 |
4.2. Пространственная оптимизация: проекты не поддаются дроблению.
В этом случае задача сводится к задаче линейного программирования с булевыми переменными, в которой требуется максимизировать суммарный NPV программы, не выходя за пределы выделенных средств IC0.
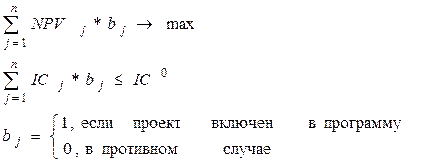
Оптимальную комбинацию находят либо просмотром всех возможных вариантов сочетания проектов, либо используя различные методы решения таких задач.
Пример 8.
В условиях Примера 7 составить оптимальную инвестиционную программу.
Решение:
| Вариант | Суммарная инвестиция | Суммарный NPV |
| А+Б | 50=30+20 | 5,19=2,51+2,68 |
| А+Г | 45=30+15 | 3,88=2,51+1,37 |
| Б+Г | 35=20+15 | 4,05=2,68+1,37 |
| В+Г | 55=40+15 | 6,19=4,82+1,37 |
Оптимальной является инвестиционная программа, включающая проекты В и Г.
