Метод корректировки нормы дисконта

Для определения нормы дохода существует формула:

E = E_min+ I + r

Выделяют статистический и экспертный методы обоснования рисковой премии в составе нормы дохода. Выбор определяется наличием (или отсутствием) статистического материала, позволяющего оценить закономерности наступления рискового события. Таким образом можно оценивать риски, связанные с надежностью работы оборудования, качеством выпускаемой продукции, поскольку возможно получение информации о вероятности отказов, аварий при эксплуатации, браке и других потерях. Статистические закономерности можно установить по природным рискам, связанным со стихийными бедствиями, авариями.

Статистический метод вычисления рисковой премии

С помощью агрегированного метода рисковая премия оценивается укрупненно по всем видам рисков.

Рассмотрим пример применения статистического метода для вычисления рисковой премии r. В данном случае она определяется как среднее квадратическое отклонение внутренней нормы дохода. Пример взят из учебника Римера М.И. и др.¹

Пример 1

Выбор менее рискованного инвестиционного проекта и обоснование рисковой премии с помощью статистического метода оценки риска.

Возможны два альтернативных варианта инвестирования 100 тыс.р. сроком на 1 год и пять возможных сценариев надежности работы оборудования в прогнозируемом периоде, характеризующихся различным уровнем риска. Данные сценарии основаны на статистической информации о поломках оборудования в предыдущие периоды в аналогичных ситуациях. Наступление каждого из вариантов с определенной вероятностью имеет соответствующую внутреннюю норму дохода.

¹ Ример М.И., Касатов А.Д., Матиенко Н.Н. Экономическая оценка инвестиций. — СПб: Питер, 2005. — 480 с.

В качестве ключевого показателя эффективности инвестиций выберем внутреннюю норму рентабельности (IRR).

Расчет ожидаемой внутренней нормы дохода (IRR) и показателя риска r

								IRRi по	(IRR -			)2 ×w
								IRR	i
		Сценарий	Количествослучаевнаступлениярезультата	Относительнаячастота			инвестициям %	i
		wi	Проект1	Проект2	Проект1			Проект2
		0,05	-3,0	-2,0	9,25		11,25
		0,20	7,0	8,0	2,59		5,00
		0,50	11,0	14,0	0,08		0,50
		0,20	14,0	16,0	2,31		1,80
		0,05	21,0	26,0	5,41		8,45
	Итого		1,00			19,64		27,00
		=åwi × IRRi , %
	IRR					10,60	13,00
Среднее квадратичное отклонение s = r	4,43	5,20
Коэффициент вариации V = s /				0,42	0,40
IRR

По проекту 2 дисперсия равна 27,0 (значение сложно интерпретировать, так как единица измерения — процент в квадрате). Стандартная девиация при этом составила 5,2%, т.е. каждый сценарий в среднем будет иметь IRR, отличающуюся от средней по данной инвестиционной альтернативе на ± 5,2% . Эта величина и есть рисковая премия, учитываемая при формировании нормы дохода: r = 5.2% .

Пользуясь только стандартным отклонением, нельзя сравнивать альтернативы с различной доходностью. Используют относительный показатель риска — коэффициент вариации, отношение стандартной девиации к ожидаемой IRR. Для проекта 2 коэффициент вариации составит 0,40. Это меньше, чем для проекта 1.

Вывод: при оценке абсолютного риска проект 2 кажется более рискованным (самое высокое значение стандартной девиации), но если учесть относительный риск, то более рискованным окажется проект 1 (наибольшее значение коэффициента вариации).

Кроме агрегированного метода, рассмотренного выше, использование статистического метода оценки риска возможно на основе поэлементного подхода. Он учитывает каждый вид риска в отдельности: определяет номенклатуру рисков, подлежащих отражению в норме дохода, оценивает влияние каждого из них на величину рисковой премии.

Общий недостаток статистических методов оценки риска заключается в необходимости наличия большого массива исходных данных для расчета, который трудно получить. Поэтому на практике при оценке рисковой премии часто используют экспертный метод.

4.5.2 Экспертный метод оценки рисковой премии

Содержание экспертного метода состоит в обработке мнений специалистов о величине рисковой премии в целом по проекту или по отдельным наиболее вероятным, с их точки зрения, видам рисков.

Возможно использование экспертного метода для оценки при поэлементном расчете рисковой премии (по видам рисков). Одна из классификаций факторов и размеров рисковой премии приведена в таблице.

В таблице в основном отражены риски, связанные с разработкой новой техники. Однако

в ней присутствуют и виды рисков, не имеющие статистической закономерности проявления и, следовательно, не поддающиеся прогнозированию. Такие риски не следует учитывать при формировании нормы дохода. Методы их учета в инвестиционном проектировании рассмотрены далее.

Величина рисковой премии в зависимости от вида риска

№		Факторы и виды риска	Прирост
			премии за
			риск, %
	Необходимость проведения НИОКР (с заранее неиз-
	вестными результатами) силами специализированных
	научно-исследовательских и (или) проектных организа-
	ций:	3–6
	· продолжительность НИОКР менее 1 года
	· продолжительность НИОКР свыше 1 года
		Ø НИОКР выполняется силами одной специализи-	7–15
		рованной
		Ø НИОКР имеет комплексный характер и выполня-	11–20
		ется несколькими организациями
	Характеристика применяемой технологии
	·	традиционная
	· новая, требующая ресурсов, имеющихся на свобод-	2–4
	·	ном рынке	5–10
	новая, требующая монополизированных ресурсов
	·	новая, исключающая использование монополизиро-	1–3
		ванных ресурсов
	Неопределенность объемов спроса и цен на производи-
	мую продукцию:
	·	существующую	0–5
	·	новую	5–10
	Нестабильность (цикличность) спроса на продукцию	0–5
	Неопределенность внешней среды при реализации про-	0–5
	екта (природные условия)
	Неопределенность процесса применения техники и тех-	0–3
	нологии

Экспертный метод широко используют для определения агрегированной рисковой премии (без разделения ее по видам рисков). При этом необходимо учитывать целевую направленность инвестиций, новизну и сложность применяемого оборудования. Для установления примерных размеров рисковой премии можно воспользоваться материалами исследования ряда американских промышленных компаний, дифференцирующими норму дохода в зависимости от класса инвестиций. Учитывая, что уровень минимально приемлемой (безрисковой) нормы дохода за рубежом составляет приблизительно 5% (ориентир — доходность 30-летнего государственного займа правительства США), можно определить размер рисковой премии по перечисленным классам инвестиций, вычитая из соответствующего значения нормы дохода величину безрисковой составляющей.

Иностранные инвесторы стремятся в величине рисковой премии учесть страновый риск, при этом для России рекомендуется повышать безрисковую норму дохода в 2 раза.

Определение величины рисковой премии в зависимости от класса инвестиций

№	Класс инвестиций	Норма	Размер
		дохода,	рисковой
		%	премии,
			%
	Вложения с целью сохранения позиций на
	рынке (в повышение качества продукции, рек-
	ламу)
	Инвестиции на обновление основных фондов
	Инвестиции с целью экономии текущих затрат
	(на базе новых технологических решений)
	Вложения с целью увеличения доходов (для
	проектов, направленных на расширение произ-
	водства на новой технологической основе на
	стабильном рынке)
	Венчурные инвестиции (в инновационные
	проекты)

Примечание

В заключение отметим недостатки метода корректировки нормы дисконта:

1. Принцип включения рисковой премии в норму дохода в методическом плане является не вполне корректным. При таком решении происходит смешение двух несовместимых подходов к расчету одного показателя. При расчете дисконтных коэффициентов

процедура капитализации дохода по правилу сложных процентов может относиться только к тем элементам, которые напрямую зависят от времени, т.е. минимально приемлемой норме (реальной) и инфляции. Что касается риска, т.е. возможной потери части дохода в связи с наступлением рискового события, то он не может быть подвержен капитализации; по правилу сложных процентов, его наступление имеет статический характер на каждом шаге возможного его проявления. Подобные элементы нельзя агрегировать в показателе, предназначенном для учета неравноценности денежных потоков во времени.

2. Этот метод фактически предполагает увеличение риска во времени с постоянным коэффициентом, что вряд ли может считаться корректным, так как для многих проектов характерно наличие рисков в начальные периоды с постепенным снижением их к концу реализации. Таким образом, прибыльные проекты, не предполагающие со временем существенного увеличения риска, могут быть оценены неверно и отклонены.

3. Данный метод не несет никакой информации о вероятностных распределениях будущих потоков платежей и не позволяет получить их оценку.

4. Наконец, обратная сторона простоты метода состоит в существенных ограничениях возможностей моделирования различных вариантов, которое сводится к анализу зависимости критериев NPV, IRR и др.от изменений только одного показателя — нормы дисконта.

Несмотря на отмеченные недостатки, метод корректировки нормы дисконта широко применяется на практике.

Достоинства метода заключаются в простоте расчетов, а также в понятности и доступности.

4.6 Метод достоверных эквивалентов (коэффициентов достоверности)

В отличие от предыдущего метода в этом случае осуществляют корректировку не нормы дисконта, а ожидаемых значений потока платежей CF путем введения специальных понижающих коэффициентов a_t для каждого периода реализации проекта.

at =	CCFt	, at £ 1.	(1)
	CFt

где CCF_t — величина чистых поступлений от безрисковой операции в период t;

CF_t —ожидаемая(запланированная)величина чистых поступлений от реализации проекта в период t.

Тогда достоверный эквивалент ожидаемого платежа может быть определен как:

CCFt = at CFt .

(2)

Таким образом, осуществляется приведение ожидаемых поступлений к величинам платежей, получение которых практически не вызывает сомнений и значения которых могут быть определены более или менее достоверно либо точно.

На практике для определения значений коэффициентов a_t чаще используется метод экспертных оценок. В этом случае коэффициенты отражают степень уверенности специалистов-экспертов в том, что поступление ожидаемого платежа осуществится.

После того, как значения коэффициентов определены, осуществляется расчет критерия

NPV:

T	a CF
NPV =å	t t	- c0,	(2)
(1 + E)t
t =1

где CF_t — суммарный поток платежей в период t; c₀—начальные инвестиции;

T —срок проекта.

Предпочтение отдается тому проекту, по которому величина NPV больше.

Пример.

Предприятие оценивает риск проекта, первоначальные затраты по которому составят 100 тыс. руб. ожидаемые чистые поступления от реализации проекта равны 50 тыс., 60 тыс. и 40 тыс. руб. В результате опроса экспертов получены следующие значения коэффициентов достоверности: 0.9, 0.85 и 0.6 соответственно. Ставка дисконта E = 8%.

Расчет скорректированного потока платежей осуществляется следующим образом:

t				CFt	at	atCFt	NPVt
	(1 + E)t
		1,0000	-100 000	1,00	-100 000	-100 000,00
		0,9259	50 000	0,90	45 000	41 666,67
		0,8573	60 000	0,85	51 000	43 724,28
		0,7938	40 000	0,60	24 000	19 051,97
						ИТОГО	4 442,92

4.7 Учет риска при анализе чувствительности проекта

Цель анализа чувствительности состоит в сравнительном анализе влияния различных факторов инвестиционного проекта на ключевой показатель эффективности проекта, например, внутреннюю норму прибыльности.

Предрисковая оценка чистых выгод инвестиционного проекта, анализ его эффективности базируется на утверждении о наиболее успешном осуществлении и эксплуатации проекта. Основываясь на ретроспективном анализе, исследователь прогнозирует определенную величину (оценку) исследуемого фактора (переменной). Однако при этом результативный проектный показатель, зависящий от данного фактора, также принимает определенное точечное значение, которое может ввести в заблуждение, так как при некотором внепрогнозном изменении переменной изменится и результативность проекта.

Необходим более тщательный количественный анализ проекта. Одним из средств, позволяющих более подробно выяснить степень влияния переменных на конечный результат, является анализ чувствительности.

Приведем наиболее рациональную последовательность проведение анализа чувствительности.

1. Выбор ключевого показателя эффективности инвестиций, в качестве которого может служить внутренняя норма прибыльности (IRR) или значение дохода (NPV).

2. Выбор факторов, относительно которых разработчик инвестиционного проекта не имеет однозначного суждения (т.е. находится в состоянии неопределенности). Типичными являются следующие факторы:

· капитальные затраты и вложения в оборотные средства,

· рыночные факторы — цена товара и объем продажи,

· компоненты себестоимости продукции,

· время строительства и ввода в действие основных средств.

3. Установление номинальных и предельных (нижних и верхних) значений неопределенных факторов, выбранных на втором шаге процедуры. Предельных факторов может быть несколько, например ± 5% и ±10% от номинального значения. Обычная процедура анализа чувствительности предполагает изменение одного исходного показателя за один расчет, в то время как значения остальных считаются постоянными величинами.

4. Расчет ключевого показателя для всех выбранных предельных значений неопределенных факторов.

5. Построение графика чувствительности для всех неопределенных факторов. В западном инвестиционном менеджменте этот график носит название “Spider Graph”.

Данный график позволяет сделать вывод о наиболее критических факторах инвестиционного проекта, с тем чтобы в ходе его реализации обратить на эти факторы особое внимание с целью сократить риск реализации инвестиционного проекта. Так, например, если цена продукции оказалась критическим фактором, то в ходе реализации проекта необходимо улучшить программу маркетинга и (или) повысить качество товаров. Если проект окажется чувствительным к изменению объема производства, то следует уделить больше внимания совершенствованию внутреннего менеджмента предприятия и ввести специальные меры по повышению производительности. Наконец, если критическим оказался фактор материальных издержек, то целесообразно улучшить отношение с поставщиками, заключив долгосрочные контракты, позволяющие, возможно, снизить закупочную цену сырья.

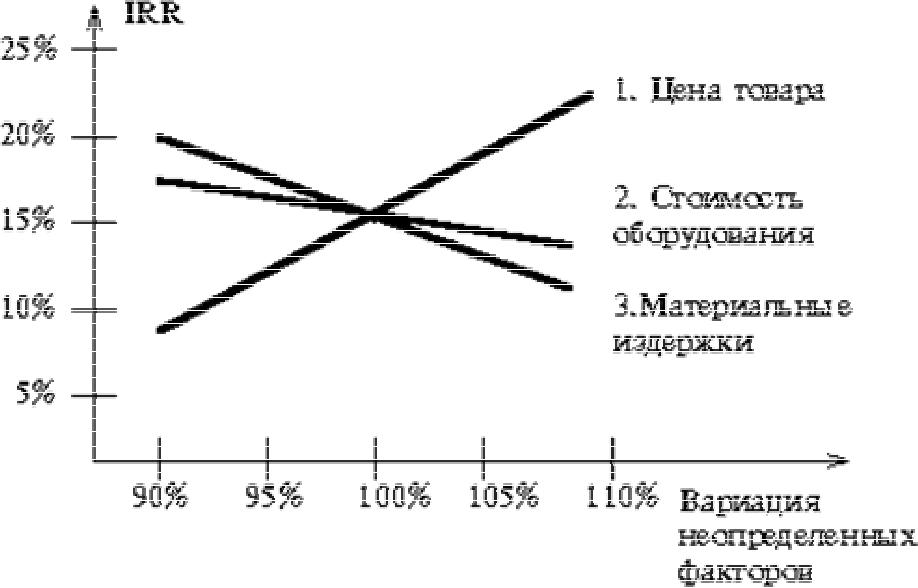
Рис 1. Spider Graph —Чувствительность проекта к изменению неопределенных факторов

Данный метод является хорошей иллюстрацией влияния отдельных исходных факторов на конечный результат проекта. С помощью анализа чувствительности можно определить зависимость проекта от таких факторов риска, как изменение спроса на продукцию, цен на продукцию и ресурсы, темпов инфляции, курса национальной валюты, процентных ставок по кредитам, себестоимости, продолжительности инвестиционного цикла и т.д.

В процессе анализа чувствительности риск непосредственно не измеряется. Вместо этого определяется устойчивость проекта к изменению значения параметров. Чем выше степень устойчивости, тем меньше его риск. Таким образом, проект с меньшей чувствительностью NPV к изменению параметров считается менее рисковым.

Главным недостатком данного метода является предпосылка о том, что изменение одного фактора рассматривается изолированно, тогда как на практике все экономические факторы в той или иной степени коррелированны.

Пример.

Рассмотрим инвестиционный проект, рассчитанный на 3 этапа. Пусть, что все предполагаемые издержки по проекту производятся единовременно в начале реализации проекта и составляют 25 000:

c₀=25 000 .

Считается, что диапазоны изменения будущих денежных поступлений от проекта и диапазон изменения коэффициента дисконтирования определены методом экспертной оценки и даны в следующей таблице:

Переменная	Диапазон	DCF ,DE			,
CF
E
CF1	8 000–10 000	1 000		9 000
CF2	18 000–24 000	3 000		21 000
CF3	28 000–32 000	2 000		30 000
Е	0,10–0,14	0,02		0,12

Определить

1. Чувствительность проекта по отношению к изменению ставки дисконта Е и потоков платежей CF_t .

2. Вероятность того, что NPV проекта будет не меньше 17 000.

Как и ранее, обозначим через CF_t разности между поступлениями и издержками на шаге m,т.е.

CF_t = b_t - c_t .

В соответствии с этим будем считать, что величина NPV является функцией переменных

CF₁,K, CF_T , E, c₀:

NPV = NPV (CF1,K, CFT , E, c0 ).

(1)

При этом величины CF₁, K, CF_T , E считаются случайными, а величину начальных издержек с₀ можно считать детерминированной. Предполагаемые диапазоны изменений величин CF₁,K, CF_T , E ,длины которых равны соответственно2DCF₁,K, 2DCF_T , 2DE ,даны в условии. Середины этих диапазонов обозначим через CF1, K, CF T , E . Тогда математическое ожидание величины чистого дисконтированного дохода равно

T

CF t

E(NPV ) = NPV (CF1, K, CF T , r , c

) =

- c

,

(2)

tå=1 (1+

)t

E

а длина предполагаемого диапазона изменения NPV равна

T

¶ NPV (CF1,K, CFT , r , c0)

¶ NPV (CF1,K, CFT , r , c0)

DNPV =

DE +å

DCFt ,

¶E

t =1

¶CFt

Вычислим производные, входящие в формулу (3):

T

¶ NPV (CF1,K, CFT , r , c0)

t × CFt

= -å

,

(1+ E)t +1

¶E

t =1

¶ NPV (

CF

1, K,

CF

T ,

r

, c

0

)

=

.

¶Ft

(1 + E)t

Подставив эти выражения в формулу (3), получим

æ T

t × CFt

ö

T

ç

÷

DNPV =çå

÷× DE +

å

× DCFt ,

(4)

(1+ E)

t +1

(1

+ E)

t

èt =1

ø

t =1

При уровне значимости a = 1/ 9 полагаем s (NPV ) = D NPV / 3.

1. Определим чувствительность проекта по отношению к изменению ставки дисконта Е. В качестве меры чувствительности примем коэффициенты эластичности NPV по Е и

CF_t .В соответствии с формулой(4)имеем

æ T

ö

t × CF t

DNPVE =

ç

å

÷

× DE

ç

÷

t +1

(1 + E )

èt =1

ø

Коэффициент эластичности по E определяется по формуле

DNPV

.

ЭE =

E

Учитывая формулы (2) и (5), получим

DE NPV

T

t × CF t

E

ЭE =å

×

,

t +1

T

(5)

(1+ E )

CF t

t =1

å

- c0

(1+ E )t

t =1

Далее, определим чувствительность по отношению к изменению денежных потоков