ЗАДАЧА 3. Аналитический поиск наилучшего решения

Полезные советы

§ Алгоритм поиска должен предусматривать дискретное изменение координат распределителя, т.е. имитацию его перемещения в заданных габаритах пространства с заданным шагом 0,1 м.

§ На каждом шаге следует вычислять суммарную длину коммуникаций ДК(м). Поскольку все участки коммуникаций параллельны осям координат и петли отсутствуют, можно применить формулу:

;

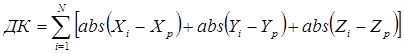где: N – количество потребителей;

i – порядковый номер потребителя;

X_i , Y_i , Z_i – координаты i – го потребителя (м);

X_p , Y_p , Z_p – координаты распределителя (м).

ЗАДАЧА 2. Поиск наилучшего решения в условиях многокритериальной

оценки вариантов

Цель: выбрать предпочтительный вариант оборудования (X или Y) с учётом показателей, приведённых в табл. 3:

№	Показатели (П)	Базовый вариант	Предлагаемые варианты
Вариант X	Вариант Y
	Производительность	100 %	130 %	90%
	Ресурс	100 %	90 %	120%
	Стоимость	100 %	120 %	110%
	Трудоемкость обслуживания	100 %	100 %	90%
	Опасность для окружающей среды	100 %	90 %	80%
	Эргономичность (уровень шума)	100 %	110 %	90%

Подсказка: можно использовать комплексный критерий оценки эффективности вариантов в виде весовой функции:

К = B₁ ^. П_пр1/П_б +B₂ ^. П_пр2/П_б +B₃ ^. П_б/П_пр3 +B₄ ^. П_б/П_пр4 +B₅ ^. П_б/П_пр5 +B₆ ^. П_б/П_пр6

- весовые коэффициенты Вi назначьте методом экспертных оценок, соблюдая условие нормировки: SBi = 1

ЗАДАЧА 3. Аналитический поиск наилучшего решения

Рис.2 Дороги и бездорожье

Подсказка:Алгоритм решения задачи может выглядеть так:

1. Найти аналитическую зависимость времени в пути t от заданных параметров АВ, ВС,Vл, Vш и искомого отрезка BD.

2. Продифференцировать это выражение по параметру BD и приравнять производную 0:

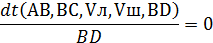
3. Подставить в полученное уравнение заданные значения АВ, ВС,Vл, Vш и найти искомое значение ВD.

4. Вычислить время t .

5. Ответить на вопрос 2.

ЗАДАЧА 4. Поиск наилучшего варианта путём трансформации объекта

Дана прямоугольная комната с размерами, показанными на рис.3.

На потолке, на расстоянии 1 м от торцевой стены и от боковых стен сидит таракан Т. На полу, на расстоянии 1 м от противоположной торцевой стены и от боковых стен, лежит крошка хлеба К.

Определите траекторию кратчайшего пути таракана к пище (без прыжков и падений) и вычислите её длину.

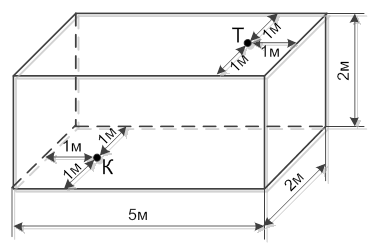
Рис. 3 Комната с тараканом

Подсказка: нужно преодолеть косность традиционного мышления и преобразовать объект к виду, удобному для решения поставленной задачи.

ЗАДАЧА 5. Выбор варианта при неопределённости критерия

Когда сын падишаха повзрослел, настало время найти ему невесту. В результате первого этапа кастинга совет мудрецов отобрал четырёх самых лучших девушек. Окончательный выбор производил сам принц. Каждой из претенденток он задал один и тот же вопрос: сколько будет дважды два?

Первая претендентка сказала: «4». Вторая сказала: «5». Третья сказала: «не знаю». А четвёртая ответила: «сколько принцу будет угодно, столько и будет».

Вопрос: какую из девушек выбрал принц?

Комментарий: за этой сказочной историей стоит множество недоразумений и недопониманий, встречающихся в достаточно серьёзных ситуациях.

ЗАДАЧА 6. Выбор варианта при равнозначности оценок

Классическая задача, которую в теории принятия решений называют задачей о Буридановом осле.

Ровно посередине между двумя совершенно одинаковыми копнами сена стоит осёл. Он не может выбрать, к какой из них нужно подойти, и, в конце концов, умирает от голода.

Какой алгоритм выбора надо применить для его спасения?