Примеры решения типовых задач
Тема: «Статистическая сводка и группировка»
Задача
Условие: Имеются данные о затратах времени клиентов на оформление путевки в туристической компании, мин.:
14, 10, 19, 24, 27, 30, 23, 20, 16, 18, 13, 15, 21, 20, 25, 28, 25, 18, 18, 12, 17, 20, 22, 21, 17, 11, 16, 21, 23, 24, 24, 19.
Постройте интервальный вариационный ряд распределения клиентов по затратам времени на оформление туристической путевки, образовав 5 равных, закрытых интервалов. Результаты группировки представьте в виде таблицы и графически.
Решение:
Для определения величины интервала найдем минимальное и максимальное значения затрат времени: 10 и 30, соответственно. Количество групп (интервалов) – 5. Тогда, величина интервала:
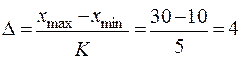
Границы интервалов: 10-14; 14-18; 18-22; 22-26; 26-30.
Распределим все имеющиеся значения по полученным группам:
| группы по величине затрат времени | затраты времени, мин. |
| 10-14 | 10, 13, 12, 11 |
| 14-18 | 14, 16, 15, 17, 17, 16 |
| 18-22 | 19, 20, 18, 21, 20, 18, 18, 20,21, 21, 19 |
| 22-26 | 24, 23, 25, 25, 22, 23, 24, 24 |
| 26-30 | 27, 30, 28 |
Итоговая таблица будет выглядеть следующим образом.
Распределение клиентов по затратам времени на оформление путевки в туристической компании
| группы по величине затрат времени, мин. | число клиентов |
| 10-14 | |
| 14-18 | |
| 18-22 | |
| 22-26 | |
| 26-30 | |
| итого |
Графически интервальный ряд распределения изображается с помощью гистограммы, где по оси ОХ откладываются значения признака, а по оси ОУ – число единиц, попавших в соответствующий интервал.
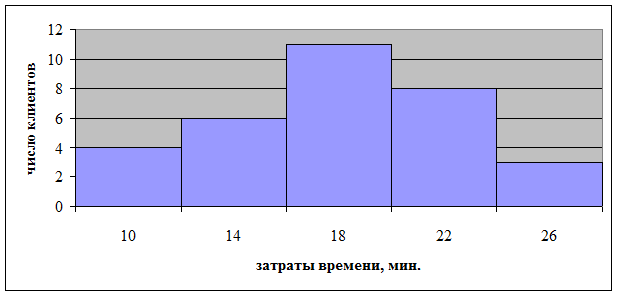
Вывод: По представленным данным было построено распределение клиентов туристической фирмы по затратам времени на оформление путевки. В результате и в таблице, и на графике видно, что чаще всего затраты на оформление путевки составляют от 18 до 22 минут – 11 клиентов из 32. 10 клиентов потратили меньше времени, 11 – больше.
Тема: «Обобщающие статистические показатели».
Задача
Условие: Данные о численности и заработной плате рабочих завода:
| № цеха | численность рабочих | доля женщин в общей численности рабочих, % | средняя заработная плата 1 рабочего, руб. |
| 4 000 | 38 000 | ||
| 1 700 | 32 000 | ||
| 5 500 | 36 000 |
Определите средние величины всех показателей, приведенных в таблице.
Решение:
Средняя численность рабочих цеха определяется по средней арифметической простой, т. к. это абсолютный показатель:
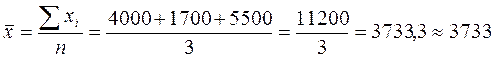
Средняя численность рабочих цеха составляет 3 733 человека.
Среднюю долю женщин рассчитаем по формуле средней арифметической взвешенной, в качестве весов будем использовать численность рабочих:
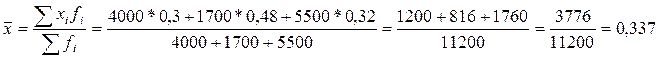Доля женщин среди рабочих по всему заводу составляет 33,7%.
Средняя заработная плата рассчитывается также по средней арифметической взвешенной (вес – численность рабочих):
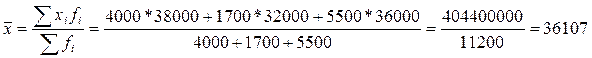
Средняя заработная плата рабочих завода составляет 36107 рублей.
Тема: «Изучение вариации».
Задача
Условие: Имеются следующие данные, характеризующие жилищные условия жителей города:
| Жилая площадь, приходящаяся на 1 человека, м2 | число жителей |
| до5 | |
| 5-10 | |
| 10-15 | |
| 15-20 | |
| 20-25 | |
| 25-30 | |
| 30 и более | |
| итого |
Определите: 1) средний размер жилой площади, приходящейся на 1 жителя города; 2) модальное и медианное значение жилой площади, приходящейся на 1 жителя города; 3) долю жителей, имеющих менее 10 кв. м. на 1 человека; 4) среднее квадратическое отклонение и коэффициент вариации изучаемого показателя; 5) децильный коэффициент дифференциации значения жилой площади, приходящейся на 1 жителя города. Постройте график данного распределения, сделайте выводы по полученным результатам.
Решение:
Для расчета среднего показателя преобразуем исходный интервальный вариационный ряд в дискретный путем определения середин каждого интервала. При этом размер открытых интервалов возьмем равными следующему и предыдущему соответственно.
| Жилая площадь, приходящаяся на 1 человека, м2 | число жителей | xi | xifi | Si | xi2fi |
| до5 | 2,5 | 20,0 | 50,00 | ||
| 5-10 | 7,5 | 712,5 | 5 343,75 | ||
| 10-15 | 12,5 | 2550,0 | 31 875,00 | ||
| 15-20 | 17,5 | 4725,0 | 82 687,50 | ||
| 20-25 | 22,5 | 4725,0 | 10 612,53 | ||
| 25-30 | 27,5 | 3575,0 | 98 312,50 | ||
| 30 и более | 32,5 | 2697,5 | 87 668,75 | ||
| итого | - | 19005,0 | 412 250,00 |
1) Рассчитаем среднюю арифметическую взвешенную:
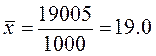м2 на 1 жителя.
2) Для нахождения модального значения необходимо определить интервал с наибольшей частотой: от 15 до 20 с частотой 270.
Теперь подставим соответствующие значения в формулу моды:
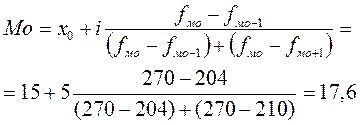
Медианное значение признака находится в середине ранжированного ряда значений, поэтому, сначала строят ряд накопленных частот, последовательно суммируя частоты от интервала к интервалу – Si (см. таблицу). Для нахождения интервала, в котором находится медиана, нужно сумму всех частот разделить пополам и найти полученное значение в ряду накопленных частот. Значит искомая накопленная частота – 500, она находится в интервале от 15 до 20. Используя формулу медианы, найдем ее значение:
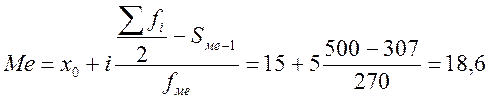
3) Доля жителей, имеющих меньше 10 кв. м. на человека, есть отношение численности жителей двух первых интервалов к общей численности жителей:
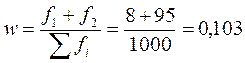
4) Для расчета среднего квадратического отклонения воспользуемся вторым способом расчета дисперсии:
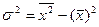
Построим дополнительную расчетную графу в таблице, а затем подставим итоговое значение в формулу:
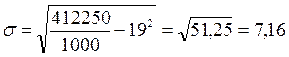
Коэффициент вариации рассчитаем по формуле:
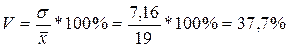
5) Для расчета децильного коэффициента дифференциации найдем первую и девятую дециль, используя ряд накопленных частот и соответствующие формулы. Первая дециль находится во втором интервале от 5 до 10, т.к. именно там расположена 100-я единица.
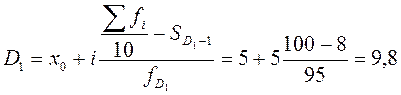м2
Девятую дециль находим в ряду накопленных частот по значению 900 (1000/10*9), это предпоследний интервал от 25 до 30.
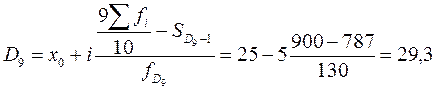м2
Децильный коэффициент дифференциации составит:
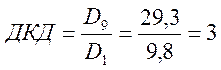
График интервального вариационного ряда – гистограмма, где по оси ОХ откладываются значения границ интервалов по жилой площади, приходящейся на 1 жителя города, а по оси ОУ – число жителей.
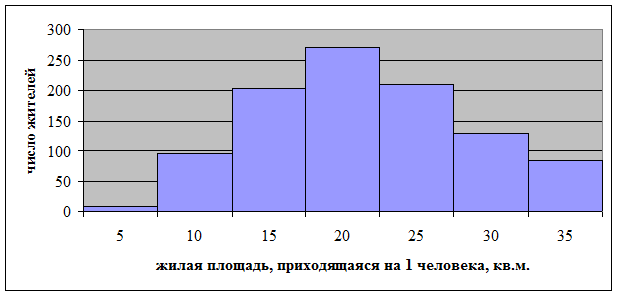
Вывод: В результате проведенного исследования установлено, что средний размер жилой площади на 1 человека по обследованной 1000 жителей составляет 19 кв. метров, при этом наиболее часто встречается значение – 17,6 кв. м/чел., а всю совокупность обследованных делит на две равные части значение 18,6 кв. м., т.е. половина жителей имеет меньше 18,6 кв. м. на человека, а другая половина больше этого значения. Доля жителей, имеющих размер жилой площади менее 10 кв. м. на 1 человека, составила 10,3%. Индивидуальные значения жилой площади в среднем отклоняются от среднего значения (19 кв.м.) на 7,19 кв. м., коэффициент вариации превышает 33%, поэтому данную совокупность жителей нельзя считать однородной по размеру жилой площади на 1 человека. 10% жителей имеют меньше 9,8 кв. м. на человека, другие 10% жителей имеют больше 29,3 кв. м. на человека. Соответственно, наименьшее из 10% наибольших значений в 3 раза больше наибольшего из 10% наименьших. Гистограмма наглядно демонстрирует распределение жителей по размеру жилой площади, приходящейся на 1 человека.
Тема: «Выборочное наблюдение»
Задача
Условие: Данные предыдущей задачи считать результатом 5-процентного бесповторного выборочного обследования. С вероятностью 0,95 (t=1,6) определить доверительные интервалы для среднего размера жилой площади, приходящейся на 1 жителя города, и доли жителей, имеющих менее 10 квадратных метров жилой площади на 1 человека. Сделайте выводы.
Решение:
Определим численность населения города. 5% выборочной совокупности составили 1000 жителей, значит численность всех жителей – 20 000 человек (следовательно, генеральная совокупность - 20 000 человек). Рассчитаем среднюю ошибку выборки для бесповторного отбора:
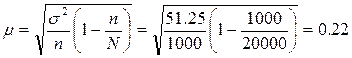м2
Тогда, предельная ошибка выборки при вероятности 0,95 составит:
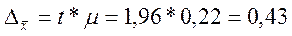м2
Доверительный интервал для средней:
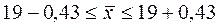
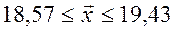
Для расчета ошибки выборки для доли необходимо определить дисперсию альтернативно признака:
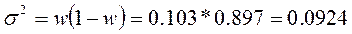
Тогда, средняя ошибка для доли:
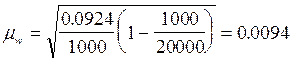
А предельная ошибка с учетом заданной вероятности:
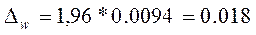
Доверительный интервал для доли:
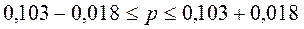
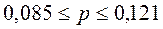
Если выразить в процентах, то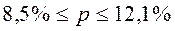 
Вывод:
С вероятностью 0,95 можно утверждать, что средний размер жилой площади, приходящейся на 1 жителя всего города, находится в пределах от 18,57 до 19,43 квадратных метров, а доля лиц, имеющих менее 10 м2 на человека, в целом по городу находится в пределах от 8,5 до 12,1%.
Тема: «Изучение динамики».
Задача
Условие: Имеются данные о числе детских дошкольных учреждений в г. Санкт-Петербурге:
| годы | ||||||
| число ДОУ |
Рассчитать цепные и базисные показатели динамики: абсолютное изменение, коэффициенты и темпы роста, темпы прироста; среднее число ДОУ за период 2005-2010 гг., средние показатели изменений числа ДОУ. Представьте динамический ряд графически. Сделайте выводы.
Решение: Для расчета показателей динамики используем следующие формулы. Абсолютное изменение: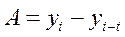 
, коэффициент изменения 
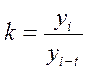, темп изменения (темп роста) 
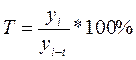, темп прироста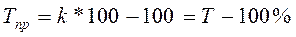 
Причем, при расчете цепных показателей уровень каждого года сравниваем с уровнем предыдущего года, а при расчете базисных показателей все уровни сравниваются с одним и тем же – 2005 года.
Результаты вычислений представим в таблице:
| годы | число ДОУ | абсолютное изменение, ед. | коэффициент роста | темп роста, % | темп прироста, % | ||||
| цеп | баз | цеп | баз | цеп | баз | цеп | баз | ||
| - | - | - | - | - | - | - | - | ||
| -44 | -44 | 0,9610 | 0,9610 | 96,10 | 96,10 | -3,90 | -3,90 | ||
| -9 | -53 | 0,9917 | 0,9530 | 99,17 | 95,30 | -0,83 | -4,70 | ||
| -49 | 1,0037 | 0,9566 | 100,37 | 95,66 | 0,37 | -4,34 | |||
| -40 | 1,0083 | 0,9645 | 100,83 | 96,45 | 0,83 | -3,55 | |||
| -33 | 1,0064 | 0,9707 | 100,64 | 97,07 | 0,64 | -2,93 |
Среднее число ДОУ за период 2005-2010 гг. рассчитаем по средней арифметической простой:
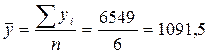
Среднее абсолютное изменение:
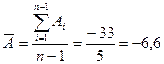
Средний коэффициент изменения по формуле средней геометрической:
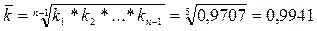
Средний темп изменения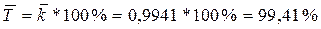 
Средний темп прироста составил: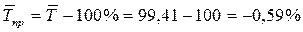 
Графически данный динамический ряд может быть представлен либо линейной, либо столбиковой диаграммой.
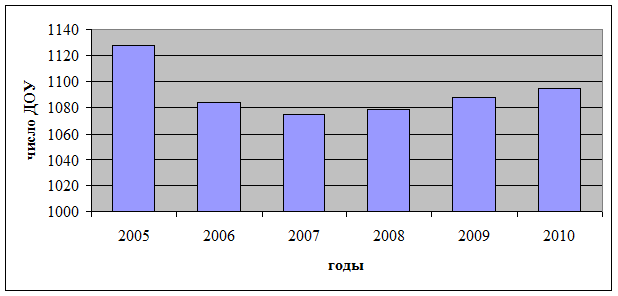
Вывод: За период с 2005 по 2010 годы наблюдалось изменение числа детских дошкольных учреждений в г. Санкт-Петербурге. В 2006 и 2007 годах число ДОУ снизилось по сравнению с предыдущим годом на 44 и 9 единиц соответственно или на 4 и 0,83%. После 2007 года количество ДОУ начало увеличиваться, но темпы этого увеличения не высоки и даже в 2010 г. число ДОУ по сравнению с 2005 г. было на 33 заведения или на 2,93% меньше, чем в 2005 г. Среднегодовое число ДОУ за рассматриваемый период составило 1091,5. Среднегодовые показатели говорят о том, что в среднем в год происходило снижение данного показателя на 6,6 единицы в год или на 0,59%.
Тема: «Методы изучения взаимосвязей».
Задача
Условие: Имеются следующие данные по некоторым европейским странам:
| № | страна | ВВП на душу населения, долл. США по ППС | доля расходов на питание, % | |
| Люксембург | 8,1 | |||
| Великобритания | 8,5 | |||
| Ирландия | 8,6 | |||
| Австрия | 9,6 | |||
| Германия | 9,8 | |||
| Дания | 10,1 | |||
| Нидерланды | 10,7 | |||
| Норвегия | 10,9 | |||
| Швеция | 11,2 | |||
| Финляндия | 11,9 | |||
| Франция | 12,2 | |||
| Бельгия | 12,5 | |||
| Исландия | 12,8 | |||
| Испания | 13,1 | |||
| Мальта | 13,6 | |||
| Словения | 13,6 | |||
| Италия | 13,7 | |||
| Кипр | 13,7 | |||
| Чехия | 14,1 | |||
| Венгрия | 15,1 | |||
| Португалия | 15,4 | |||
| Греция | ||||
| Словакия | 16,2 | |||
| Польша | 18,2 | |||
| Латвия | 18,4 | |||
| Эстония | 20,9 | |||
| Болгария | ||||
| Литва | 23,3 | |||
| Румыния | 26,6 | |||
| Россия | 28,8 | |||
| Македония | 30,5 |
Используя ранговые коэффициенты, оцените степень тесноты связи между уровнем ВВП на душу населения и долей расходов на питание. Дайте графическое изображение предполагаемой зависимости. Сделайте выводы.
Решение:
Рассчитаем коэффициенты Фехнера и Спирмена.
Для расчета первого коэффициента необходимо определить средние значения по обоим признакам.
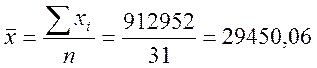
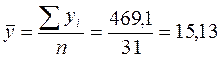
Теперь сравниваем каждое значение со средним и определяем знак отклонения (графы 5, 6 в расчетной таблице). Если знаки отклонений совпадают, то в графе 7 ставим «С» - совпадение; если нет, то ставим «Н» - несовпадение. Подставляем общее количество совпадений и несовпадений в формулу и рассчитываем значение коэффициента:
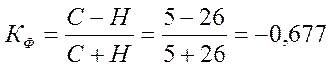
Для расчета коэффициента Спирмена необходимо проранжировать значения по каждому признаку. Присвоим ранги от наименьшего до наибольшего (графы 8, 9 а расчетной таблице), а затем по каждой строке определим разницу и рангов и возведем ее в квадрат (графа 10). Подставим необходимые значения в формулу и рассчитаем результат.
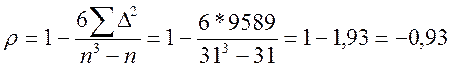
Расчетная таблица
| страна | ВВП на душу населения, долл. США по ППС | доля расходов на питание, % | отклонение | С/Н | ранги | ||||
| X | Y | X | Y | ||||||
| Люксембург | 8,1 | + | - | н | |||||
| Великобритания | 8,5 | + | - | н | |||||
| Ирландия | 8,6 | + | - | н | |||||
| Австрия | 9,6 | + | - | н | |||||
| Германия | 9,8 | + | - | н | |||||
| Дания | 10,1 | + | - | н | |||||
| Нидерланды | 10,7 | + | - | н | |||||
| Норвегия | 10,9 | + | - | н | |||||
| Швеция | 11,2 | + | - | н | |||||
| Финляндия | 11,9 | + | - | н | |||||
| Франция | 12,2 | + | - | н | |||||
| Бельгия | 12,5 | + | - | н | |||||
| Исландия | 12,8 | + | - | н | |||||
| Испания | 13,1 | + | - | н | |||||
| Мальта | 13,6 | - | - | с | 15,5 | 12,25 | |||
| Словения | 13,6 | + | - | н | 15,5 | 2,25 | |||
| Италия | 13,7 | - | - | с | 17,5 | 0,25 | |||
| Кипр | 13,7 | - | - | с | 17,5 | 6,25 | |||
| Чехия | 14,1 | - | - | с | |||||
| Венгрия | 15,1 | - | - | с | |||||
| Португалия | 15,4 | - | + | н | |||||
| Греция | - | + | н | ||||||
| Словакия | 16,2 | - | + | н | |||||
| Польша | 18,2 | - | + | н | |||||
| Латвия | 18,4 | - | + | н | |||||
| Эстония | 20,9 | - | + | н | |||||
| Болгария | - | + | н | ||||||
| Литва | 23,3 | - | + | н | |||||
| Румыния | 26,6 | - | + | н | |||||
| Россия | 28,8 | - | + | н | |||||
| Македония | 30,5 | - | + | н | |||||
| 469,1 |
Графически взаимосвязь между двумя признаками может быть представлена в виде корреляционного поля:
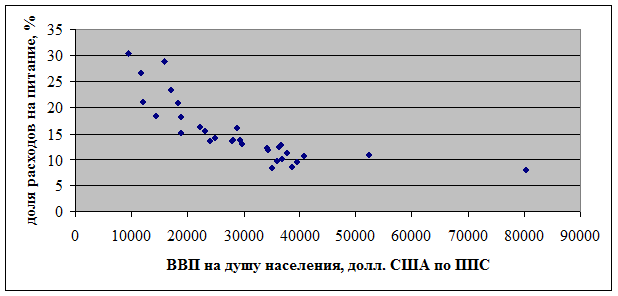
Вывод: Проанализировав значения двух показателей по основной части европейских государств можно сказать, что между ВВП на душу населения и долей расходов на питание наблюдается связь, она обратная и достаточно сильная. Это подтверждается отрицательными значениями полученных коэффициентов, по абсолютному значению приближающиеся к единице. Кроме того, тесную обратную связь видно на графике, где точки расположены близко друг к другу, направление поля сверху вниз и слева направо.
Тема: «Статистика населения»
Задача
Условие: Представлены некоторые данные о численности и движении населения РФ:
| Показатель, тыс. чел. | ||||
| численность населения на начало года | 141914,5 | |||
| численность родившихся | 1311,6 | 1476,2 | 1717,5 | 1788,9 |
| численность умерших | 2254,9 | 2165,7 | 2028,5 | |
| в том числе детей до 1 года | 19,1 | 14,5 | 13,4 | |
| число заключенных браков | 1001,6 | 1113,7 | 1178,7 | 1215,1 |
| число зарегистрированных разводов | 763,5 | 640,9 | 703,4 | 639,3 |
| число прибывших | 193,5 | 186,4 | 281,6 | 191,7 |
| число выбывших | 121,2 | 54,1 | 39,5 | 33,6 |
Рассчитать:
1) численность населения на конец года
2) среднегодовую численность населения
3) общие коэффициенты естественного движения населения:
рождаемости, смертности, естественного прироста, брачности, разводимости
4) коэффициент нетто-миграции, коэффициент общего прироста
5) специальные коэффициенты: жизненности и младенческой смертности.
Решение:
1) Численность населения на конец года определим по следующей формуле:
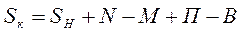
Для 2001 численность на конец года составит
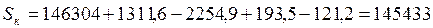тыс. чел.
2) Среднегодовая численность населения рассчитывается по средней арифметической простой:
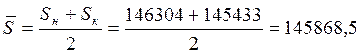тыс. чел.
3) Общие коэффициенты естественного движения населения рассчитываются соотнесением соответствующего абсолютного значения со среднегодовой численностью населения и умножением результата на 1000.
Общий коэффициент рождаемости
‰
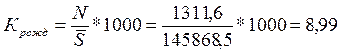Общий коэффициент смертности
‰
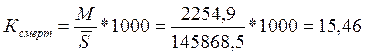Общий коэффициент естественного движения
‰
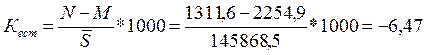Общий коэффициент брачности
‰
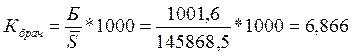Общий коэффициент разводимости
‰
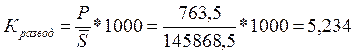4) Коэффициент нетто-миграции рассчитывается соотнесением сальдо миграции и среднегодовой численности населения, выражается в промилле
‰
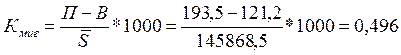Коэффициент общего прироста может быть рассчитан как сумма коэффициентов естественного и миграционного движения
‰
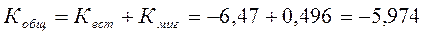5) Коэффициент жизненности Покровского отражает процесс замещения выбывающих поколений вновь появляющимися
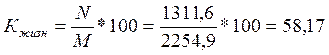
Коэффициент младенческой смертности как социальный индикатор, может быть рассчитан соотношением умерших до 1 года с численностью родившихся
‰
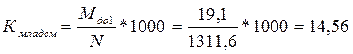Результаты аналогичных вычислений за другие годы представлены в таблице:
| показатель | ||||
| численность на конец года, тыс чел. | 145433,0 | 142196,8 | 141887,6 | |
| среднегодовая численность населения, тыс. чел. | 145868,5 | 142475,4 | 141948,3 | 141873,8 |
| коэффициент рождаемости, ‰ | 8,99 | 10,42 | 12,01 | 12,61 |
| коэффициент смертности, ‰ | 15,46 | 15,2 | 14,66 | 14,3 |
| коэффициент естественного прироста, ‰ | -6,47 | -4,84 | -2,65 | -1,69 |
| коэффициент брачности, ‰ | 6,866 | 7,817 | 8,304 | 8,565 |
| коэффициент разводимости, ‰ | 5,234 | 4,498 | 4,955 | 4,506 |
| коэффициент нетто-миграции, ‰ | 0,496 | 0,929 | 1,706 | 1,114 |
| коэффициент общего прироста, ‰ | -5,974 | -3,911 | -0,944 | -0,576 |
| специальный коэффициент жизненности,% | 58,17 | 68,16 | 82,53 | 88,19 |
| специальный коэффициент младенческой смертности, ‰ | 14,56 | 10,16 | 8,44 | 7,49 |
Выводы: В результате представленных вычислений можно сказать, что наблюдается уменьшение численности населения РФ за период с 2001 по 2010 годы. Это снижение происходит за счет естественного движения – естественная убыль населения (коэффициент естественного движения отрицательный). При этом следует отметить, что наблюдается снижение темпов убыли: в 2001 г. коэффициент естественного движения (-6,47‰,), а в 2010 г. – (-1,69‰). Это подтверждает и коэффициент жизненности Покровского: в 2001 г. на 100 умерших рождалось 58 человек, в 2010 г. на 100 умерших рождалось 88 человек. Снижение численности населения за счет естественной убыли частично компенсируется миграционным движением, происходит увеличение сальдо миграции. Однако даже в 2010 г. коэффициент нетто-миграции не превышает коэффициент естественной убыли, и наблюдается общее сокращение численности населения (коэффициент общего прироста отрицательный (-0,576‰). Специальный коэффициент младенческой смертности показывает долю не доживших до 1 года из общего числа родившихся и характеризует уровень социального развития общества, медицины в нем. В 2010 г. из 1000 родившихся 7,5 детей не доживали до 1 года. С 2001 по 2010 г. наблюдается снижение этого показателя в РФ почти в 2 раза.
Тема: «Статистика занятости и безработицы»
Задача
Условие: Имеются следующие данные по области, тыс. чел.:
Среднегодовая численность занятых в материальном производстве …………………………………………………………1550
Численность занятых в сфере услуг
на начало года …………………………………………………750
на конец года …………………………………………………..770
Среднегодовая численность безработных …………………….75
Среднегодовая общая численность населения ……………..4800
Определите:
1) среднегодовую численность активного населения;
2) коэффициент экономически активного населения;
3) уровень занятости;
4) уровень безработицы.
Решение:
1) Сначала определим среднегодовую численность занятых в сфере услуг: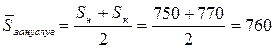 
тыс. чел.
Численность экономически активного населения составляют занятые и безработные, поэтому:
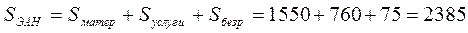тыс. чел.
2) Коэффициент экономически активного населения:
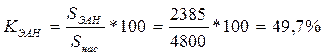
3) уровень (коэффициент) занятости:
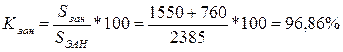
4) уровень (коэффициент) безработицы:
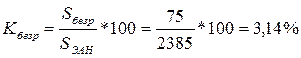
или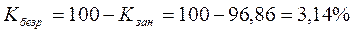 
Вывод: Численность экономически активного населения в области составила 2385 тыс. чел., это составляет почти половину от всего населения региона. Уровень занятости – 96,86%, а уровень безработицы только 3,14%.
Тема: «Статистика доходов и расходов населения»
Задача
Условие: Имеются следующие данные.
Распределение общей суммы начисленной заработной платы
по 10-процентным группам работников по РФ
| номер группы | ||
| 1 (с наименьшей заработной платой) | 2,1 | |
| 3,2 | ||
| 3,2 | 4,3 | |
| 4,3 | 5,4 | |
| 5,6 | 6,6 | |
| 7,1 | 7,9 | |
| 8,9 | 9,5 | |
| 11,8 | 11,9 | |
| 17,2 | 15,7 | |
| 10 (с наибольшей заработной платой) | 38,9 | 33,4 |
Рассчитать коэффициенты Лоренца, Джини. Построить кривую Лоренца. Сделать выводы о степени дифференциации работников по уровню заработной платы.
Решение:
Воспользуемся формулами для расчета коэффициентов: Лоренца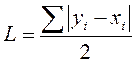 
Джини
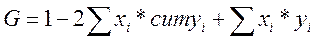
Произведем промежуточные вычисления в таблицах отдельно для каждого года.
2001 год
| № группы | xi | yi | |yi-xi| | cum yi |
| 3,2 | 6,8 | 6,2 | ||
| 4,3 | 5,7 | 10,5 | ||
| 5,6 | 4,4 | 16,1 | ||
| 7,1 | 2,9 | 23,2 | ||
| 8,9 | 1,1 | 32,1 | ||
| 11,8 | 1,8 | 43,9 | ||
| 17,2 | 7,2 | 61,1 | ||
| 38,9 | 28,9 | |||
| итого | 100,0 | 75,8 | 297,1 |
2011 год
| № группы | xi | yi | |yi-xi| | cum yi |
| 2,1 | 7,9 | 2,1 | ||
| 3,2 | 6,8 | 5,3 | ||
| 4,3 | 5,7 | 9,6 | ||
| 5,4 | 4,6 | |||
| 6,6 | 3,4 | 21,6 | ||
| 7,9 | 2,1 | 29,5 | ||
| 9,5 | 0,5 | |||
| 11,9 | 1,9 | 50,9 | ||
| 15,7 | 5,7 | 66,6 | ||
| 33,4 | 23,4 | |||
| итого | 100,0 | 339,6 |
Для 2001 года коэффициент Лоренца составит:
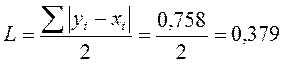
Коэффициент Джини для 10-ти процентных групп может быть упрощен
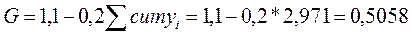
Для 2011 года коэффициент Лоренца:
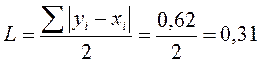
Коэффициент Джини:
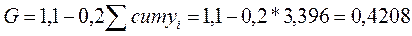
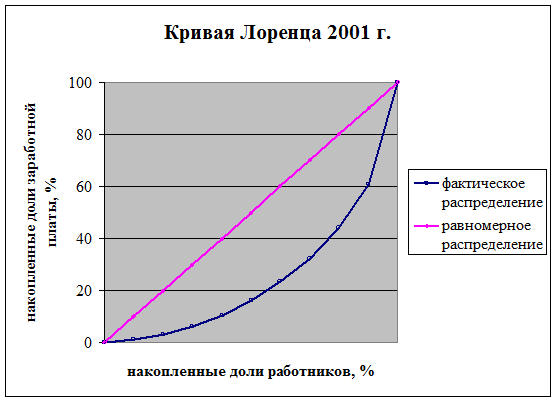
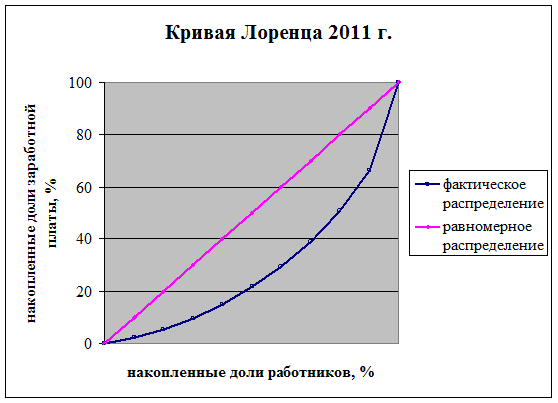
Выводы:
Значения коэффициентов Лоренца (0,379 и 0,31) и Джини (0,5058 и 0,4208) свидетельствуют о существенной степени дифференциации работников в РФ по уровню заработной платы. При этом в 2011 г. по сравнению с 2001 г. степень дифференциации заметно сократилась.
Тема: «Статистика потребления»
Задача
Условие: Имеются следующие данные о структуре потребительских расходов населения г. Санкт-Петербурга:
| статьи | удельный вес, % | |
| покупка продуктов питания | 59,5 | 33,0 |
| покупка непродовольственных товаров | 22,0 | 38,2 |
| покупка алкогольных напитков | 2,1 | 2,4 |
| оплата услуг | 16,4 | 26,4 |
| 100,0 | 100,0 |
Оценить степень концентрации структуры потребительских расходов в 1995 и 2005 гг. Дать анализ структурных изменений потребительских расходов населения в 2005 г. по сравнению с 1995 г.
Решение:
Для оценки степени концентрации рассчитаем соответствующий коэффициент:
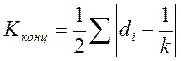
| статьи | удельный вес, % |  | ||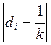
| покупка продуктов питания | 59,5 | 33,0 | 34,5 | 8,0 |
| покупка непродовольственных товаров | 22,0 | 38,2 | 3,0 | 13,2 |
| покупка алкогольных напитков | 2,1 | 2,4 | 22,9 | 22,6 |
| оплата услуг | 16,4 | 26,4 | 8,6 | 1,4 |
| итого | 100,0 | 100,0 | 69,0 | 45,2 |
1995 г.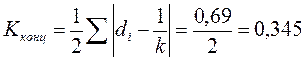 
2005 г.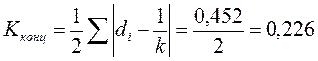 
При изучении двух структур используются следующие коэффициенты: индекс различий, интегральный коэффициент структурных сдвигов К. Гатева. Для расчета этих коэффициентов выполним промежуточные расчеты (см. таблицу).
| номер группы | удельный вес, % |  |  |  |  | |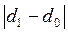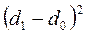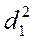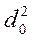
| 59,5 | 33,0 | 26,5 | 702,25 | 3540,25 | ||
| 22,0 | 38,2 | 16,2 | 262,44 | 484,00 | 1459,24 | |
| 2,1 | 2,4 | 0,3 | 0,09 | 4,41 | 5,76 | |
| 16,4 | 26,4 | 10,0 | 100,00 | 268,96 | 696,96 | |
| итого | 100,0 | 100,0 | 53,0 | 1064,78 | 4297,62 | 3250,96 |
Индекс различий:
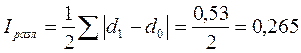
Интегральный коэффициент структурных сдвигов К. Гатева:
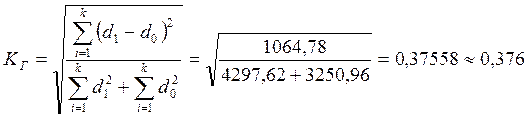
Кроме полученных коэффициентов используются абсолютные измерители структурных изменений - линейный и квадратический коэффициенты абсолютных структурных сдвигов. Они показывают, на сколько процентных пунктов в среднем отклоняются друг от друга сравниваемые удельные веса.
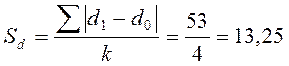
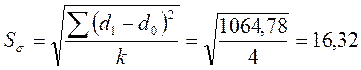
Выводы: Степень концентрации в структуре потребительских расходов населения Санкт-Петербурга в 1995 г. высокая – коэффициент концентрации составил 0,345, это объясняется наличием доминирующей группы – покупка продовольственных товаров – 59%. В 2005 г. степень концентрации существенно снизилась – 0,226. За 10 лет произошли существенные изменения в структуре потребления, подтверждаемые полученными коэффициентами. Индекс различий – 0,265, интегральный коэффициент структурных различий Гатева – 0,376. В абсолютном выражении удельные веса групп в структуре потребления в 2005 г. по сравнению с 1995 г. изменились в среднем на 13,25 п.п. (по коэффициенту) или 16,32п.п. (по среднеквадратическому коэффициенту).
Тема: «Статистика системы здравоохранения и здоровья населения»
Задача
Условие: В результате проведенного в регионе 10-ти процентного выборочного наблюдения получены следующие данные:
| заболеваемость населения всеми болезнями на 1000 чел. | количество населенных пунктов |
| 500-600 | |
| 600-700 | |
| 700-800 | |
| 800-900 | |
| 900 и выше | |
| итого |
Определить уровень заболеваемости населения по всему региону (уровень значимости 0,954).
Решение:
Определим значение средней по выборке и среднее квадратическое отклонение.
| заболеваемость населения всеми болезнями на 1000 чел. | количество населенных пунктов | середина интервала |  |  |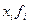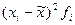
| 500-600 | ||||
| 600-700 | ||||
| 700-800 | ||||
| 800-900 | ||||
| 900 и выше | ||||
| итого |
Средняя заболеваемость по выборке:
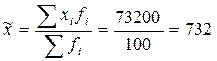
Среднее квадратическое отклонение:
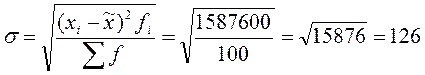
Средняя ошибка выборки при 10-ти процентном отборе составит: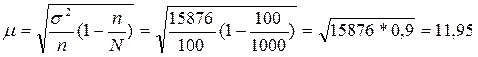 
Предельная ошибка выборки с вероятностью 0,954:
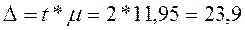
Тогда, доверительные интервалы для выборочной средней:
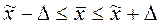
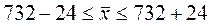
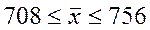
Вывод: В результате проведенного выборочного наблюдения можно сказать, что средняя заболеваемость населения составила 732 на 1000 человек при среднем квадратическом отклонении – 126.
С вероятностью 0,954 можно утверждать, что средний уровень заболеваемости по региону находится в пределах от 708 до 756 заболеваний на 1000 человек населения.
Тема: «Статистика системы и уровня образования»
Задача
Условие: Имеются следующие данные о численности детей и числе мест в дошкольных образовательных учреждениях г. Санкт-Петербурга:
| годы | численность детей, тыс. чел. | число мест, тыс. ед. |
| 130,7 | 124,5 | |
| 131,6 | 125,8 | |
| 134,6 | 126,6 | |
| 139,6 | 126,9 | |
| 146,8 | 133,3 | |
| 157,4 | 140,1 | |
| 163,7 | 148,2 | |
| 169,2 | 155,1 | |
| 177,7 | 163,3 |
Произведите сравнительный анализ динамики двух представленных показателей за период 2002-2010 гг.
Решение:
Сначала произведем оценку средних уровней данных показателей. Средняя численность детей в ДОУ составила:
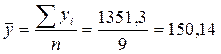
Среднее число мест в ДОУ: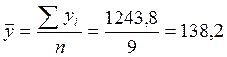 
Соотношение этих средних 150,14/138,2*100%= 108,6% означает, что за анализируемый период средняя численность детей в ДОУ Санкт-Петербурга превышает среднее количество мест в них на 8,6%.
Для сравнительного анализа динамики следует использовать средние и относительные показатели динамики.
Рассчитаем средние абсолютные изменения по численности детей в ДОУ и числу мест в ДОУ в г. Санкт-Петербурге за период с 2002 по 2010 гг. По численности детей:
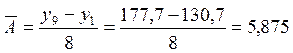
По числу мест:
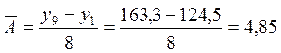
Средние темпы изменения за изучаемый период. По численности детей:
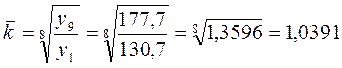
По числу мест:
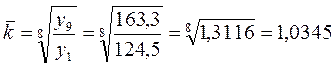
Следовательно, за период с 2002 по 2010 годы происходил рост обоих показателей, но численность детей в ДОУ увеличивалась в среднем в год на 5875 человек или на 3,91%, а число мест в них на 4850 или на 3,45%.
Для детального сравнения динамики по каждому году можно использовать коэффициенты опережения, рассчитываемые соотношением цепных темпов роста (см. таблицу).
| годы | численность детей, тыс. чел. | число мест, тыс. ед. | темпы роста, % | коэффициент опережения | |
| численность детей | число мест | ||||
| 130,7 | 124,5 | ||||
| 131,6 | 125,8 | 100,7 | 101,0 | 0,9965 | |
| 134,6 | 126,6 | 102,3 | 100,6 | 1,0163 | |
| 139,6 | 126,9 | 103,7 | 100,2 | 1,0347 | |
| 146,8 | 133,3 | 105,2 | 105,0 | 1,0011 | |
| 157,4 | 140,1 | 107,2 | 105,1 | 1,0202 | |
| 163,7 | 148,2 | 104,0 | 105,8 | 0,9832 | |
| 169,2 | 155,1 | 103,4 | 104,7 | 0,9876 | |
| 177,7 | 163,3 | 105,0 | 105,3 | 0,9975 |
Дополнительной иллюстрацией этой динамики может служить график цепных темпов роста обоих показателей.
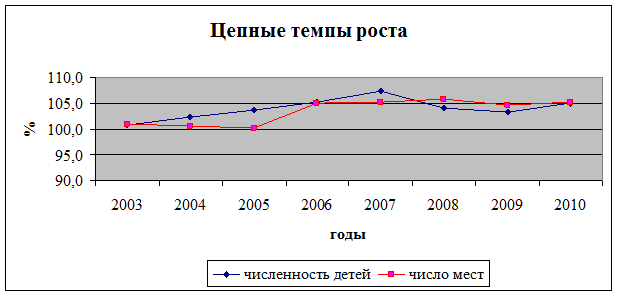
Выводы:
За последние 9 лет численность детей в дошкольных образовательных учреждениях превышает число мест в них на 8,6%. За этот период оба показателя увеличивались, но разными темпами. В среднем численность детей в ДОУ увеличивалась на 5875 человек или на 3,91% в год, а число мест в них на 4850 или на 3,45%. Большую часть рассматриваемого периода темпы роста численности детей превышали темпы роста мест в ДОУ, следовательно, в ближайшей перспективе превышение численности детей в дошкольных образовательных учреждениях г. Санкт-Петербурга над числом мест в них сохранится при условии сохранения динамики обоих показателей.
Контрольные вопросы по второй части курса (социальная статистика):
1. Предмет и задачи социальной статистики.
2. Предмет статистики населения (демографической статистики).
3. Общие и специальные демографические коэффициенты, используемые для изучения естественного движения населения.
4. Основные группировки населения, используемые в демографической статистике. Понятие структуры населения.
5. Анализ половозрастной структуры населения и факторов, её определяющих, с помощью возрастно-половых пирамид.
6. Понятия уровня жизни и качества жизни населения.
7. Макроэкономические индикаторы уровня жизни населения.
8. Использование баланса доходов и расходов для анализа состава, объёмов и структуры доходов и расходов населения.
9. Бюджетные обследования населения как источник информации об уровне жизни населения.
10. Диаграмма Лоренца и её аналитические возможности.
11. Содержание и техника расчёта коэффициента Джини.
12. Влияние инфляции на уровень потребления населением.
13. Бедность как категория социальной статистики. Статистические характеристики бедности.
14. Показатели и структура потребления.
15. Понятие социально опасных заболеваний.
16. Показатели состояния и развития системы здравоохранения.
17. Статистические показатели для оценки здоровья населения.
18. Количественные и неколичественные характеристики уровня образования.
19. Системы показателей, характеризующих различные ступени системы образования.
20. Источники информации о потреблении населением благ и услуг в сфере культуры.
Список литературы
1) Громыко Г.Л. Теория статистики: Практикум. – 4-е изд., доп. и перераб. – М.: ИНФРА-М, 2011.- 240 с.
2) Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник/ Под ред. чл.-корр. РАН И.И. Елисеевой. – 5-е изд., перераб. и доп.-М.: Финансы и статистика, 2004. – 656 с.
3) Елисеева И.И., Юзбашев М.М., Флуд Н.А. Практикум по общей теории статистики: Учебное пособие. - М.: Финансы и статистика, 2008. – 512 с.
4) Ефимова М.Р., Бычкова С.Г. Практикум по социальной статистике: Учебное пособие. – М.: Финансы и статистика, 2005. – 448 с.
5) Ефимова М.Р., Бычкова С.Г. Социальная статистика: Учебное пособие. – М.: Финансы и статистика, 2004. – 560 с.
6) Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: Учебное пособие – 3-е изд., перераб. и доп. - М.: Финансы и статистика, 2011 – 368 с.
7) Практикум по социальной статистике: Учебное пособие – 2-е изд., перераб. и доп.-/ Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2006 – 368 с.
8) Социальная статистика: Учебник/ Под ред. чл.-корр. РАН И.И. Елисеевой. – 3-е изд., перераб. и доп. - М.: Финансы и статистика, 2003. – 480 с.
9) Статистика: учебник/ под ред. И.И. Елисеевой. - М.: Издательство Юрайт; ИД Юрайт, 2011. – 565 с.
10) Теория статистики: Учебник/ Под ред. проф. Г.Л. Громыко. – 2-е изд., перераб. и доп. – М.: ИНФРА-М, 2010. – 475 с.
11) Издания Росстата:
a) Россия в цифрах
b) Российский статистический ежегодник
c) Регионы России. Социально-экономические показатели
d) Демографический ежегодник
e) Социальное положение и уровень жизни населения России
f) Семья в России
g) Женщины и мужчины России
h) Образование в России
i) Здравоохранение в России
и другие
12) Официальный сайт Федеральной службы государственной статистики РФ: www.gks.ru
Приложение 1