Замена платежей и сроков их выплат

Для эквивалентной замены платежей необходимо, чтобы их приведенные стоимости совпадали:

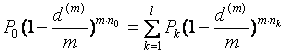. (60)

Новый срок выплат определится по формуле:

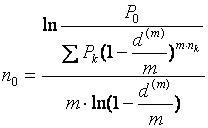. (61)

Эквивалентность простых и сложных ставок

Две ставки называются эквивалентными, если при замене одной ставки на другую финансовые отношения сторон не меняются.

Определение эквивалентной ставки основывается на решении одного из уравнений.

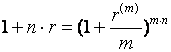 ; (62)

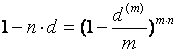 ; (63)

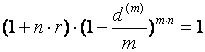 ; (64)

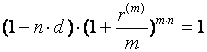 . (65)

Непрерывное наращение и дисконтирование

Непрерывное наращение и дисконтирование часто применяется при исследовании этих процессов на предельно возможные значения и в теоретических изысканиях.

Например, для процесса наращения по процентной ставке получим

,

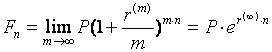где 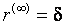называется силой роста процентной ставки или интенсивностью наращения за год. Тогда наращение за 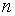лет определяется по формуле

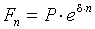. (66)

Если 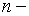неотрицательное вещественное число, то получаем непрерывное наращение:

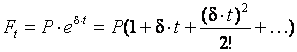. (67)

Располагая равенством

,

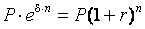получим эквивалентности:

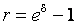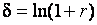; . (68)

Аналогичным образом получаем для процесса дисконтирования:

,

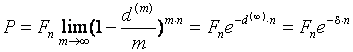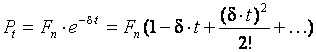, (69)

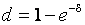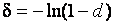, . (70)

Денежные потоки

Виды денежных потоков и задачи их анализа

На оси времени выберем множество моментов времени (рис. 5):

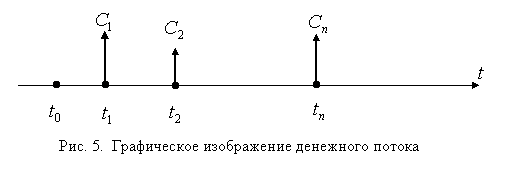
где 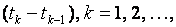- временные периоды; 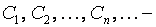денежные поступления, называемые элементами потока; если 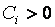, то элемент называется поступлением; если 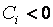, то элемент называется выплатой.

По моменту возникновения 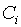потоки подразделяются на:

а) постнумерандо, если 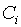возникает в момент 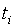, т. е. в конце 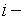го периода времени; на рис. 5 показан поток постнумерандо;

б) пренумерандо, если 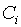возникает в момент 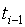, т. е. в начале 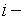го периода времени.

Замечание.

1. Обычно рассматривается поток постнумерандо с равными периодами 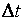; например, это может быть анализ инвестиционных проектов.

2. Поток пренумерандо – это обычно анализ схем денежного накопления для их последующего инвестирования.

К задачам анализа денежного потока относятся:

1) прямая задача – получить оценку наращенного денежного потока (будущей стоимости; при этом используется схема наращения для приведения сумм к одному моменту времени, т. к. деньги имеют временную ценность:

,

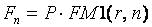где множитель наращения ;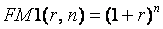

2) обратная задача – получить суммарную оценку дисконтированного (приведенного) денежного потока; при этом используется схема дисконтирования:

,

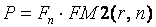где множитель дисконтирования .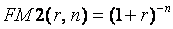

При решении этих задач используется предположение о «разумном» инвесторе, который немедленно инвестирует, а капитализация средств выполняется обычно по схеме сложных процентов.