Способ относительных разниц.
Применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида у = (а-в)*с, используемых в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.
Для мультипликативных моделей типа у = а*в*с методика анализа следующая.
1) находят относительное отклонение каждого факторного показателя:
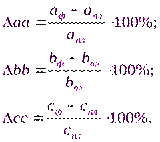
2) определяют отклонение результативного показателя у за счет каждого фактора:
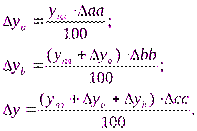
Пример 3.Воспользовавшись данными табл. 1, проведем анализ способом относительных разниц. Относительные отклонения рассматриваемых факторов составят:
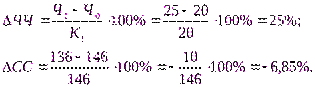
Рассчитаем влияние на объем товарной продукции каждого фактора:
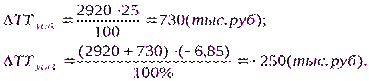
Результаты расчетов те же, что и при использовании предыдущего способа.
Способ простого прибавления неразложимого остатка.
Предполагает деление неразложимого остатка на 2 и прибавление результата к величине влияния качественного и количественного факторов. Формулы определения влияния факторов принимают вид:
Z (x) = yD0 y;Dx*Dx + ½ D*
Z (y) = xD0 y.Dx*Dy + ½ D*
Однако данный способ неприменим, если количество факторов превышает два.
Способ взвешенных конечных разностей.
При этом методе величина влияния каждого фактора определяется по всем возможным подстановкам, затем результат суммируется, и от полученной суммы берется средняя величина.
ZD1 (x) = y1 x;D*
ZD2 (x) = y0 x;D*
ZD1 (y) = x1 y;D*
ZD2 (y) = x0 y;D*
_
ZDZ (x) = ½ [D1 ZD(x) + 2 (x)];
_
ZDZ (y) = ½ [D1 ZD(y) + 2 (y)].
Логарифмический метод.
Пропорциональное распределение неразложимого остатка по факторам достигается с помощью логарифмического метода. Он позволяет определить влияние большего количества факторов на результативный показатель без установления очередности подстановок.
Способ применим к кратным и мультипликативным моделям. Он основан на логарифмировании отклонения отчетного и базисного значений результативного показателя, равного отношению соответствующих произведений факторов.
Способ долевого участия.
Способ заключается в определении доли каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост совокупного показателя. Этот метод применяется к аддитивным моделям и чаще всего для оценки влияния факторов второго или третьего порядков.
8. Интегральный метод.
Позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям. Операция вычисления определенного интеграла решается с помощью ПЭВМ и сводится к построению подъинтегральных выражений, которые зависят от вида функции или модели факторной системы.
Можно также использовать уже сформированные рабочие формулы, приводимые в специальной литературе.
1. Модель вида у = а*b:
Δуа = Δа *bо +1/2 Δа*Δb;
Δуb = Δb ао + ½ Δа*Δb.
2. Модель вида у = а * b * с :
Δуа = ½ Δа*(b0 c1+b1с0) + 1/3 Δа* Δb*Δс;
Δуb= ½ Δb*(аос1 +а1с0) + 1/3 Δа*Δb*Δс;
Δуc = ½ Δс* (ао b1+ а1 b0)+ 1/3 Δа*Δb *Δс.
3. Модель вида у = а/в:
Δуа = Δа/ Δb * ln Ib1/ b0I;
Δуb = Δbобщ - Δуа;
Интегральный метод позволяет достигнуть полного разложения результативного показателя и поровну разделить между факторами его дополнительный прирост.
