Тема 4. Маркетинговые исследования
Задание 4
Предприятие, выпускающее стиральные машины, провело опрос репрезентативной группы покупателей целевого сегмента рынка. Опрос позволил определить совокупность свойств (микроатрибутов), возникающих в памяти потребителей стиральных машин, и количественно выразить важность этих атрибутов для каждого из опрошенных. В результате статистической обработки массива полученных данных были выявлены его главные компоненты (факторы) и определена корреляционная связь каждого исходного атрибута с выявленными факторами. Было также установлено, что первые три фактора объясняют 85% общей вариации исходных данных. Результаты анализа приведены в табл. 1. Используя результаты анализа,
представьте в графическом виде корреляционные связи микроатрибутов с выявленными факторами;
сделайте содержательную интерпретацию выявленных факторов.
Методические рекомендации к выполнению задания 4
Когда факторы многомерных статистических данных определены, становится возможным получение графического представления взаимосвязи факторов и исходных микроатрибутов, проецируя последние на факторные планы, образуемые парами перпендикулярных друг другу факторов.
Такое построение не является обязательным, но оно целесообразно, поскольку значительно облегчает анализ и интерпретацию факторов.
Для отражения исходных микроатрибутов на этом плане используют значения коэффициентов их корреляции с каждым из факторов (с учетом знака). Коэффициенты корреляции определяют координаты точки-микроатрибута на факторном плане. Условный пример такого построения приведен на рис. 1.
Таблица 1
Результаты факторного анализа данных опроса покупателей стиральных машин
| Обоз-наче- ние | Микроатрибуты | Коэффициенты корреляции исходных атрибутов с факторами | ||
| Фактор 1 (45%) | Фактор 2 (25%) | Фактор 3 (15%) | ||
| А1 | Срок службы | 0,69 | 0,12 | 0,44 |
| А2 | Торговая марка товара | 0,65 | -0,17 | 0,14 |
| А3 | Оригинальность формы и исполнения | -0,76 | 0,23 | -0,16 |
| А4 | Доступная цена | 0,21 | 0,31 | 0,85 |
| А5 | Широта дополнительных функций | 0,34 | 0,87 | 0,28 |
| А6 | Цвет | -0,62 | 0,36 | -0,12 |
| А7 | Срок гарантии | 0,71 | 0,22 | 0,56 |
| А8 | Производительность | 0,45 | 0,57 | 0,61 |
| А9 | Безотказность | 0,74 | 0,61 | 0,31 |
| А10 | Экономный расход стирального порошка | 0,14 | 0,28 | 0,74 |
| А11 | Потребляемая электроэнергия | 0,18 | -0,29 | 0,68 |
| А12 | Наличие послепродажного сервиса | 0,31 | 0,76 | 0,21 |
| А13 | Размеры | 0,09 | 0,58 | 0,1 |
| А14 | Вес | 0,15 | 0,49 | 0,09 |
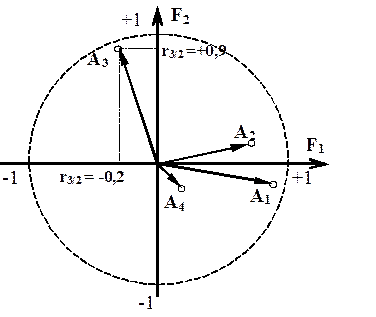
Рис. 1 - Пример факторного плана
Точки, представляющие исходные атрибуты, будут располагаться в кругес радиусом, равным 1 (так как коэффициент корреляции не выходит за пределы (-1) ...(+1). Выявленные факторы могут быть интерпретированы, исходя из тесноты корреляционной связи каждого фактора с теми или иными микроатрибутами.
На рис. 1 факторный план образован факторами F1 и F2. Другие факторные планы образуются возможными парными комбинациями других факторов.
Фактор F2 должен быть интерпретирован, исходя из его наиболее тесной связи с микроатрибутом А3, а фактор F1 - исходя из его тесной связи с микроатрибутами А1 и А2 . Микроатрибут А4 не может служить основой для интерпретации факторовF1 и F2 из-за незначительности его связи с этими факторами.
Используя для идентификации факторов F1 и F2 микроатрибуты, следует обращать внимание и на то, как эти микроатрибуты связаны с другими факторами. Желательно использовать те микроатрибуты, которые имеют менее тесную связь с другими факторами. Это позволит сделать более точную интерпретацию рассматриваемых факторов.
Задание 5
В результате проведенного исследования были получены оценки важности атрибутов (идентифицированных предварительно) для потребителей определенной категории продукции, а также оценки степени ощущаемого присутствия данных атрибутов в нескольких конкурирующих марках товара. Результаты исследования приведены в таблице 2. Используя эти результаты, определите:
состав атрибутов, которые целесообразно использовать при разработке модели формирования позиции потребителя;
продукт, который будет иметь наибольший спрос, если модель формирования позиции покупателей будет компенсационной.
Методические рекомендации к выполнению задания 5
При выполнении задания следует помнить, что позиция покупателя по отношению к продукту - это функция знания покупателем атрибутов продукта с учетом их важности (значимости) для потребителя и их ощущаемого проявления в продукте.
В обобщенном виде модель формирования позиции отдельного потребителя по отношению к продукту может быть записана следующим образом:
,
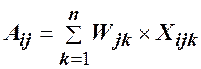где Aij - позиция j-го покупателя по отношению к i-ой марке;
Wjk - относительная значимость для j-ого потребителя k-го атрибута;
Xijk - степень ощущаемого j-м потребителем проявления k -го атрибута в i-ой марке;
n - число определяющих атрибутов.
При построении аналогичной модели для группы потребителей значения параметров модели следует брать как усредненные по группе покупателей.
Не следует забывать, что при моделировании позиции покупателя недостаточно измерения только важности атрибутов. С точки зрения их способности делать продукты отличаемыми при выборе атрибуты неодинаковы.
Таблица 2
Результаты опроса потребителей
| Потребители | Атрибут 1 | Атрибут 2 | Атрибут 3 | Атрибут 4 | ||||||||||||
| Важность атрибута | Оценка присутствия атрибута в марках товара | Важность атрибута | Оценка присутствия атрибута в марках товара | Важность атрибута | Оценка присутствия атрибута в марках товара | Важность атрибута | Оценка присутствия атрибута в марках товара | |||||||||
| А | Б | В | А | Б | В | А | Б | В | А | Б | В | |||||
| Вариант 1 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 | ||||||||||||||||
| Вариант 2 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 | ||||||||||||||||
| Вариант 3 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 | ||||||||||||||||
| Вариант 4 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 |
Продолжение таблицы 2
| Вариант 5 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 | ||||||||||||||||
| Вариант 6 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 | ||||||||||||||||
| Вариант 7 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 | ||||||||||||||||
| Вариант 8 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 | ||||||||||||||||
| Вариант 9 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 | ||||||||||||||||
| Вариант 10 | ||||||||||||||||
| Потребитель 1 | ||||||||||||||||
| Потребитель 2 | ||||||||||||||||
| Потребитель 3 | ||||||||||||||||
| Потребитель 4 |
Если уровень ощущаемого проявления атрибута одинаков во всех конкурирующих марках продуктов, то такой атрибут уже не является определяющим решение потребителя при выборе продукта определенной марки, так как не позволяет их различать. Различия в отношении покупателей к конкурирующим маркам обусловливаются именно определяющими атрибутами. Поэтому при моделировании процесса формирования отношения покупателя нецелесообразно использовать атрибуты с низкой определяющей способностью.
Определяющую способность атрибута получают, умножая усредненные итоги измерения его важности для группы потребителей на итоги измерения его различаемости (ощущаемых различий) между марками.
Различаемость атрибута может быть определена разными способами. Одним из них является определение различаемости как среднеквадратического отклонения оценок атрибута (σ) по анализируемым маркам, используя формулу:
,
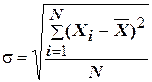где σ – показатель различаемости k -го атрибута;
Xi– оценки потребителями ощущаемого проявления k -го атрибута в анализируемым марках;
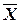– средняя оценка ощущаемого проявления атрибута в анализируемых марках;
N – количество марок.
Для выявления пропорций в определяющих способностяхкаждого атрибута рассчитывается их общая сумма, а затем показатели определяющей способности каждого атрибута делятся на их общую сумму. Полученные таким образом значения для каждого атрибута в сумме дают 1 (единицу) и могут быть представлены в процентном выражении.
При компенсационной модели формирования позиции отдельного потребителя по отношению к продукту выбранным продуктом будет тот, у которого условный количественный показатель позиции (Ai) будет наибольшим.
Задание 6
Для оптимизации плана производства предприятию, выпускающему одежду, необходимо знать, каковы пропорции в численности групп потребителей, имеющих разный рост. Чтобы получить необходимую информацию предприятие провело описательное маркетинговое исследование.
При опросе выборки потребителей каждый из них указал свой рост. Результаты опроса приведены в таблице 7.
Используя результаты опроса,
постройте гистограмму распределения частот, с которыми потребители обследованной выборки указали разные типоразмеры одежды;
рассчитайте показатели среднего значения и стандартного отклонения.
Методические рекомендации к выполнению задания 6
В маркетинговых исследованиях практически всегда возникает необходимость описать наблюдаемые переменные с помощью показателей, резюмирующих информацию.
Показателем центра группирования значений исследуемой переменной (центральной тенденции) является средние арифметическое значение наблюдаемой переменной, которое определяется по формуле:
,
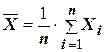деXi – наблюдаемые в выборке значенияпеременной;
n – количество наблюдений в выборке.
Для описания случайной переменной лишь один расчет среднего значения является недостаточным. Он должен сопровождаться расчетом показателей степени вариации (рассеивания)значенийслучайной величины.К ним можно отнести следующие:
диапазон наблюдаемых значений (Xmin, xmax);
стандартное отклонение (классический показатель рассеивания случайной величины);
коэффициент вариации.
Таблица
Рост респондентов выборки, см.
| Респонденты | Вариант | |||||||||
Формула расчета выборочного стандартного отклонения имеет вид:
.
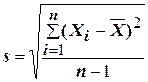Стандартное отклонение является удобным и естественным показателем рассеивания значений переменной в силу соответствия единиц его измерения с единицами измерения ее значений.
Коэффициент вариации (n) используется в тех случаях, когда степень рассеивания более естественно описывать, сопоставляя ее со средним значением и рассчитывается по формуле:
.
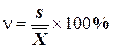Каждая из перечисленных выше характеристик степени рассеивания дает представление о том, как сильно могут отклоняться от своего центра группирования значения исследуемой случайной величины. Если говорить о графических формах представления распределения частот исследуемого признака, то для этого обычно используется специальная диаграмма, называемая гистограммой.
Пример гистограммы приведен на рис. 2.
Для построения гистограммы весь диапазон наблюдаемых в выборке значений случайной переменной (от минимального до максимального наблюдаемого значения) разбивается на несколько равных интервалов. Затем определяется количество наблюдаемых в выборке значений переменной, «попадающих» в каждый интервал. На основе подсчитанных таким образом частот, с которыми встречаются разные наблюдаемые значения переменной, строится диаграмма.
 |
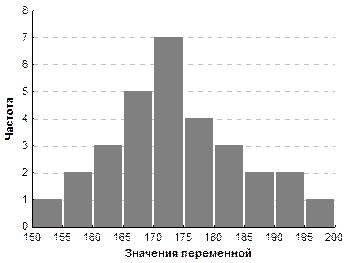По оси 0Х откладываются значения границ интервалов. По оси 0Y –частоты, с которыми отдельные значения переменной «попадают» в каждый из интервалов.
Рис. 2 – Пример гистограммы
Задание 7
Предприятию, выпускающему одежду, необходимо знать, существует ли зависимость между ростом человека и размером одежды, которую он носит. Чтобы получить необходимую информацию оно провело опрос, в ходе которого каждый респондент указал свой рост и размер одежды. Результаты опроса приведены в таблице 8.
Таблица 8
Значения роста и размера одежды, указанные респондентами
| Респондент | Вариант | |||||||||
Проанализируйте данные таблицы 8 и дайте ответ на следующие вопросы:
существует ли взаимозависимость между ростом человека и размером одежды, которую он носит?
если связь существует, то каков характер этой связи?
Методические рекомендации к выполнению задания 7
Целью объясняющих исследований рынка является установление факта существования связи между исследуемыми переменными.
Для предварительного анализа существования связи между двумя переменными целесообразно построить таблицу «пересечения» значений исследуемых переменных (перекрестную таблицу).
Чтобы ее построить, вначале необходимо разбить диапазон наблюдаемых значений на несколько равных по величине интервалов для каждой из анализируемых переменных. Число интервалов не должно быть слишком велико: максимум 3 – 4.
После этого перекрестная таблица может быть представлена в таком виде, условный пример которого приведен в таблице.
Таблица
Пример перекрестного табулирования значений двух переменных
| Интервалы значений переменной 1 | Итого | ||||
| 100 – 120 | 121 – 140 | 141 – 160 | |||
| Интервалы значений переменной 2 | 25 – 50 | ||||
| 51 – 75 | |||||
| 76 – 100 | |||||
| Итого: |
Каждая ячейка перекрестной таблицы отражает количество наблюдений (частоту), в которых значения обеих переменных соответствуют определяющим ее интервалам.
Интерпретацию перекрестной таблицы облегчают показатели структуры распределения частот совпадений значений двух переменных, выраженные в процентном отношении. Они могут быть рассчитаны двумя способами:
по отношению к итогам строк;
по отношению к итогам колонок.
В такой таблице можно увидеть, как изменяются значения одной переменной с изменением значений другой переменной и сделать выводы о наличии или отсутствии взаимозависимости между исследуемыми переменными.
Тема 4. Маркетинговые исследования
Задание 8
Для расчета доли рынка продукта питания марки «Х» производителю необходимо знать среднее значение объема его потребления одной семьей за год в натуральном выражении с точностью ± 0,25 кг и уровнях значимости 5% и 1%.
При этом известно, что объемы потребления продукта семьями с разным уровнем доходов (низким, средним и высоким) отличаются из-за различий в финансовых возможностях потребления. Данные о количестве семей с разным уровнем доходов в общей совокупности потребителей, а также о максимальном и минимальном объеме покупок ими продукта приведены в таблице.
Таблица
Количество семей с разным уровнем доходов и объемы их покупок
| Уровень доходов | Количество семей | Минимальный объем покупок, кг. | Максимальный объем покупок, кг. |
| Низкий | 0,4 | 5,7 | |
| Средний | 2,8 | 6,3 | |
| Высокий | 2,5 | 8,4 |
Наличие этих данных позволяет использовать для оценки среднего значение объема потребления продукта одну из видов случайных выборок: простую, стратифицированную пропорциональную, стратифицированную непропорциональную.
Используя имеющиеся данные, определите
размер выборки каждого из видов, необходимый для оценки среднего значения объема потребления продукта с заданной точностью и достоверностями, сравните их размеры и сделайте выводы;
определите размеры подвыборок, которые необходимо сделать из каждой страты при формировании пропорциональной и непропорциональной стратифицированных выборок.
Методические рекомендации к выполнению задания 8
Простая случайная выборка (Simple Random Sampling — SRS) - вероятностный метод выборки, согласно которому каждый элемент генеральной совокупности имеет известную и равную вероятность отбора. Каждый элемент выбирается независимо от каждого другого элемента, и выборка формируется произвольным отбором элементов из основы выборки. При простой случайной выборке исследователь сначала формирует основу выборочного наблюдения, в которой каждому элементу присваивается уникальный идентификационный номер. Затем генерируются случайные числа, чтобы определить номера элементов, которые будут включены в выборку. Эти случайные числа могут генерироваться компьютерной программой.
Простая случайная выборка не часто используется в маркетинговых исследованиях. Более популярен метод систематической выборки.
Систематическая выборка (systematic sampling) – сначала задают произвольную отправную точку, а затем из основы выборочного наблюдения последовательно выбирают каждый i-й элемент. Интервал выборки i определяется как отношение объема совокупности N к объему выборки п, с округлением результата до ближайшего целого числа. Например, совокупность состоит из 100 тысяч элементов, а желательный объем выборки равен тысяче респондентов. В этом случае интервал выборки i равен 100. Выбирается случайное число между 1 и 100. Если, например, это число равно 23, то выборка состоит из элементов 23, 123, 223, 323, 423, 523 и т.д.
Размер простой случайной выборки рассчитывается следующим образом:
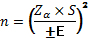 | (1) |
где, n – размер выборки, ед.;
Zα – константа, отражающая уровень погрешности (значимости) результатов;
S – среднеквадратическое отклонение в выборке или генеральной совокупности (макс – мин/6);
Е – допустимая ошибка оцениваемого параметра в единицах измерения этого параметра.
| α | 1% | 5% | 10% | 20% |
| Zα | 2,57 | 1,96 | 1,64 | 1,28 |
Часто некоторая совокупность может быть разделена на подсовокупности, отличающиеся между собой уровнем значений изучаемой переменной. Простая выборка, к сожалению, не гарантирует хорошую представительность в ней всех отличающихся подсовокупностей, существующих внутри генеральной совокупности. Поэтому простая случайная выборка не исключает возможность получить оценку изучаемого параметра очень далекую от его истинного значения.
Цель стратифицированных выборок состоит в том, чтобы повысить точность оценки, выделяя «слои» (страты), более однородные внутри себя и отличающиеся друг от друга с точки зрения диапазона возможных значений исследуемой переменной. Из–за внутренней однородности каждой из страт в них будет наблюдаться меньшая вариация изучаемого признака, чем общая вариация в генеральной совокупности. Это, в свою очередь, будет является причиной меньшей общей вариации, учитываемой при расчете размера выборки.
При составлении пропорциональной стратифицированной выборки генеральная совокупность подразделяется на взаимоисключающие и исчерпывающие подсовокупности. Критерий деления на страты должен быть выбран таким образом, чтобы изучаемые объекты были однородны внутри каждой страты с точки зрения изучаемой переменной и отличались от объектов других страт. В исследованиях массового потребителя классическим критерием стратификации является уровень доходов.
Размер пропорциональной стратифицированной выборки (n), обеспечивающей желаемую точность измерения (E) исследуемого параметра с заданным уровнем значимости (a) может быть определен по формуле:
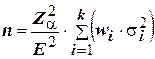, (4)
где wi– значимость (удельный вес) i –й страты в генеральной совокупности;
si – вариация значений исследуемой переменной в i –й страте;
k – количество страт.
Для определения параметра (si) можно использовать один из уже известных подходов.
Для составления пропорциональной стратифицированной выборки из каждой страты делаются простые случайные выборки таким образом, чтобы они были пропорциональны размерам страт в генеральной совокупности.
Удельный вес страты в генеральной совокупности не обязательно является наилучшим, особенно тогда, когда в каждой страте вариация изучаемой переменной существенно отличается. В стратах, где вариация небольшая можно было бы довольствоваться подвыборкой намного меньших размеров, чем это диктуется удельным весом страты. И, наоборот, там, где вариация значительна принять непропорционально бóльшую выборку, позволяющую улучшить точность оценки.
Размер непропорциональной стратифицированной выборки можно рассчитать по формуле:
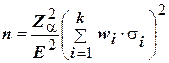. (5)
Распределение общего рассчетного числа респондентов между стратами в непропорциональной стратифицированной выборке делается с использованием следующего уравнения:
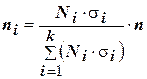, (6)
где Ni - размер i-й страты, чел.;
ni - размер выборки из i-й страты, чел.;
si - cреднеквадратическое отклонение значений исследуемого признака в i-й страте.
Задание 9
В таблице 2 представлены данные о полученных в результате опроса значениях двух дихотомических переменных - «Пол» и «Регулярность покупки продукта «А». Каждая из них принимает только одно из двух возможных значений. Переменная «Пол» принимает значения:
«Мужчина»;
«Женщина».
Переменная «Регулярность покупки продукта «А» принимает значения:
«Регулярно»;
«Иногда».
Таблица 2
Регулярность покупки продукта потребителями разного пола
| «Регулярно» | «Иногда» | ||
| Вариант 1 | Мужчины | ||
| Женщины | |||
| Вариант 2 | Мужчины | ||
| Женщины | |||
| Вариант 3 | Мужчины | ||
| Женщины | |||
| Вариант 4 | Мужчины | ||
| Женщины | |||
| Вариант 5 | Мужчины | ||
| Женщины |
Используя приведенные данные, сделайте вывод с уровнем достоверности не менее 5%,
существует ли связь между анализируемыми переменными;
если связь существует, то какова ее сила.
Методические рекомендации к выполнению задания 9
Для анализа связи между двумя дихотомическими (бинарными) переменными строятся таблицы частот, с которыми «пересекаются» градации обеих переменных (таблицы сопряженности, перекрестные таблицы). Такие таблицы имеют вид таблицы 3.
Таблица 3
Пример таблицы сопряженности градаций дихотомических переменных
| Значения переменной В(j) | |||
| B1 | B2 | ||
| Значения переменной А(i) | A1 | A1 B1 | A1 B2 |
| A2 | A2 B1 | A2 B2 |
Ai Bj – количество наблюдений выборки, в которых совпадают i-е свойство переменной A с j-мсвойством переменной B.
Вывод о существовании связи (или ее отсутствии) между двумя номинальными (в частном случае дихотомическими) переменными могут служить результаты расчета значения статистики c2.
Схема формулировки вывода о наличии (отсутствии) связи между переменными будет следующей: «Отклонить нулевую гипотезу об отсутствии связи с вероятностью ошибки (a), если расчетное значение c2 > критического».
Формула для определения расчетного значения статистики c2 выглядит следующим образом:
, (7)
где Нij – наблюдаемые в выборке частоты совпадений свойств переменных (Ai Bj );
Тij – теоретические частоты, с которыми должны совпадать свойства переменных (Ai Bj ), если справедлива гипотеза об отсутствии связи между ними;
r – число строк таблицы сопряженности (2);
c – число колонок таблицы сопряженности (2).
Теоретические частоты (Тij) совпадения свойств двух дихотомических переменных (частоты на пересечении строк i и колонок j) могут быть рассчитаны по формуле:
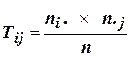, (8)
где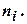 
– сумма наблюдаемых частот в каждой i-й строке;
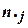– суммы наблюдаемых частот в каждой j-й колонке;
n – число наблюдений в выборке.
Число степеней свободы (k) для определения критического значения стратистики c2 рассчитывается по формуле:
k = (r – 1)×(c–1). (9)
Если значение стратистики c2, превышает критическое, что свидетельствует о наличии статистически значимой связи между двумя дихотомическими переменными, то желательно иметь коэффициент, характеризующий тесноту (силу, степень) этой связи. Такая информация может быть получена путем расчета ряда коэффициентов.
Если известно значение статистики c2, то можно рассчитать значение следующих коэффициентов:
коэффициента сопряженности (С);
коэффициента корреляции (j)
Значение коэффициента сопряженности (С) определяется по следующей формуле:
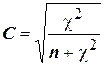. (10)
Когда ассоциативная связь между переменными отсутствует значение коэффициента сопряженности (С) тоже будет равно 0. Максимальное же значение коэффициента сопряженности при равенстве числа градаций исследуемых переменных (r = c) задается выражением:
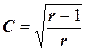. (11)
Степень связи между переменными оценивается путем сравнения расчетного значения коэффициента сопряженности с его максимально возможным значением.
С использованием данных таблицы 3, значение коэффициента корреляции (j)[1] определяется по формуле:
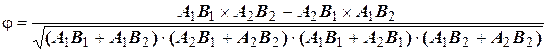. (12)
То же самое значение коэффициента можно получить, используя зависимость между значениями (j) и c2, которая определяется следующим выражением:
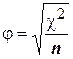. (13)
Коэффициент (j) может принимать значения от –1 до +1. Значение (0) означает отсутствие какой-либо связи. Значения (-1 или + 1), независимо от знака, означают наличие абсолютной (функциональной) связи между одними и теми же градациями анализируемых переменных, но зависит от способа представления частот их совпадения в таблице сопряженности. Например, знак (+) свидетельствует об одновременном (совместном) изменении частот совпадений градаций переменных, отражаемых в ячейках Aи D таблицы 4. Если же способ представления градаций тех же дихотомических переменных в таблице сопряженности будет изменен, как показано в таблице 5, то абсолютное значение коэффициента (j) не изменится, но он будет иметь знак (–), что не влияет на интерпретацию результатов расчета.
Задание 10
Полагая, что объемы продаж продукта зависят от размера затрат на рекламу, предприятие в течение ряда месяцев фиксировало значение этих показателей. Результаты наблюдений приведены в таблице 10. Используя эти результаты,
представьте в виде графика зафиксированные соответствия между размерами затрат на рекламу и объемами продаж;
рассчитайте коэффициенты (b и b) линейной регрессионной модели, отражающей зависимость между этими показателями и отобразите линию регрессии на том же графике; определите степень точности полученной регрессионной модели;
определите силу (тесноту) связи между анализируемыми показателями.
Методические рекомендации к выполнению задания 10
Линейная регрессионная модель зависимости между двумя переменными в общем виде может быть представлена следующим образом:
,
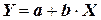где Y– зависимаяпеременная (в задании - объемы продаж)
X– независимаяпеременная (размеры затрат на рекламу);
а – постоянный коэффициент, отражающий значение Y, которое имеет место при отсутствии влияния на нее переменной X;
b – коэффициент регрессии, который количественно характеризует степень влияния изменений независимой переменной X на зависимую переменную Y (в масштабе реальных единиц их измерения).
Значения этих коэффициентов рассчитываются по формулам:
,
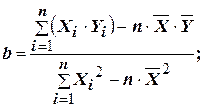
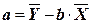где Xi, Yi– наблюдаемые значения переменных X и Y;
n – число наблюдений соответствующих друг другу пар значений переменных;
, 
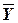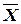– средние арифметические значения наблюдаемых переменных, соответственно Y и X. Определяются по формулам:
; 
.
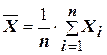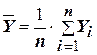Таблица 10
Результаты наблюдений объемов продаж и размеров затрат на рекламу
| Наблюдение | Варианты | |||||||||||||||||||
| Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | Объем продаж | Затраты на рекламу | |
Коэффициент b в регрессионной модели количественно отражает влияние уровня независимой переменной X на формирование уровня зависимой переменной Y с учетом реальных единиц их измерения. С изменением единиц измерения любой из переменных значения b - коэффициентов в регрессионной модели также изменятся.
Вместе с тем, часто бывает необходимо определить долю влияния независимой переменной на уровень зависимой переменной, которая остается одинаковой при любых единицах измерения переменных и для удобства интерпретации может быть выражена в процентах.
Долю влияния (в долях единицы) переменной X на формирование уровня зависимой переменной Y характеризует стандартизованный коэффициент регрессии, или b- коэффициент. Он связан с коэффициентом (b) следующим соотношением:
,
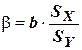где b – стандартизованный коэффициент регрессии;