Как использовать статистику

Существует резкое различие между

менеджерами, использующими расчеты и не использующими тако­вые, хотя я считал бы, что расчеты полезны всем им. Но и среди тех, кто пользуется расчетами, имеется разделение на менеджеров, осве­домленных в статистике, и тех, кто не осведомлены. Требования по­вышения качества, обычно включающие SPC (Контроль статистичес­кой обработки), повышают осведомленность в области статистики, но обычно только среди специалистов-производственников. И это очень жаль, потому что статистика может быть полезна для всех¹. Одной из наиболее полезных концепций статистики является нормальное рас­пределение, как показано на рис. 26.1, который характеризует рост мужчин в Соединенном Королевстве (UK).

Средний рост мужчин в UK (т.е. сумма величин роста всех муж­чин, деленная на количество мужчин), вероятно, составляет около 5 футов 9 дюймов (175 см). Мода роста (наиболее распространенный рост) примерно такая же. Медиана роста (такой рост, по отношению к которому мужчин меньшего роста столько же, сколько большего), вероятно, тоже близка к этой величине.

Если мы изобразим графически численность мужчин разного ро­ста (в футах и дюймах, либо в метрах) в процентах от всего населе­ния, то получим похожую на колокол кривую, представляющую нор­мальное распределение. Эта кривая симметрична относительно средней точки. Другими словами, количество мужчин ростом 5 футов 8 дюймов и ростом 5 футов 10 дюймов одинаково. Аналогично име­ется столько же мужчин (но намного меньше, чем в предыдущем слу­чае) ростом 5 футов и 6 дюймов, сколько ростом 6 футов. Опять-таки количество мужчин (теперь намного меньшее) ростом 5 футов 3 дюй­ма равно числу мужчин ростом 6 футов 3 дюйма. И наконец, будет очень мало, но тем не менее будет, мужчин ростом 5 футов и ниже, причем их число будет равно числу мужчин ростом 6 футов 6 дюймов и выше.

8-339

Рост

Численность

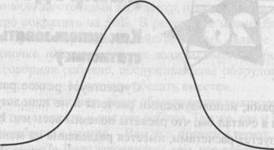
5'0" 5'3" 5'6" 5'8" 5'9"5'10"6'0" 6'3" 6'6"

Рис. 26.1. Нормальное распределение

Конечно, эта кривая, как и все модели в этой книге, идеализиро­вана. Но как и другие модели, она реалистична. Многие показатели имеют нормальное распределение, например, уровень интеллекта (IQ), для которого величина 100 составляет среднее, медиану и моду. По­этому людей с IQ, равным 85 и меньше, столько же, сколько с IQ, равным 115 и выше.

Какую практическую пользу дает нормальное распределение? Оно предоставляет нам гигантские возможности для предвидения.

Как раскрыть потенциал статистики, используя нормальное распределение

Пример 1.

В ходе реализации проекта в компании, предоставляющей финан­совые услуги, консультант по менеджменту спросил Гарри Тэйера, руководителя сектора, сколько времени занимает осуществление про­цесса корпоративного обновления.

«Сколько нам требуется времени для обновления!? - повторил Гарри Тэйер. - Это хороший вопрос». Он сделал паузу, задумчиво оглядел свой офис, заваленный бумагами, торжествующе повернулся

Т14

к консультанту и произнес: «На этот вопрос невозможно дать ответ. Обновление может занимать половину дня, а может — две недели. Невозможно установить стандартное время для такой работы».

«Я не пытаюсь установить стандартное время, я пытаюсь выяс­нить каково обоснованное время для типовой работы по обновлению».

«Но ведь не существует такой вещи, как типовое обновление», — продолжал возражать Тэйер. «Спасибо Вам, Вы мне очень помогли своим ответом», — таков был бесстрастный на вид ответ.

Во второй половине того же дня по графикам выполнения работ, извлеченным из гор документации, удалось установить продолжитель­ность предыдущих 100 обновлений. Да, пять из них заняли меньше од­ного дня, тогда как шесть - больше семи дней. Двадцать были выполне­ны менее чем за два дня, а 18 - более чем за шесть. Шестьдесят две работы этого рода потребовали для завершения от трех до пяти дней.

Представьте себе, как удивился Гарри, когда на следующее утро он увидел график продолжительности обновлений, имеющий вид нор­мального распределения, где минимум был равен двум часам, а мак­симум - двум неделям. «Ну что, Гарри, два часа или две недели?» -спросил один из его коллег, показывая на график. И продолжал: «Бери для начала четыре дня, а затем посмотри, как сократить это время до трех дней, если получится». Лицо Гарри стало пунцовым, но явно это не было связано с тем, как он провел перерыв на ланч.

Пример 2.

После определения производительности различных центров об­работки на предприятии, занимающемся поставками комплектующих для автомобильной промышленности, внутренняя рабочая группа по­ставила задачу увеличения пропускной способности до уровня, кото­рый мог бы вернуть предприятию рентабельность, а работникам -премии. В качестве первоначальной цели была выбрана пропускная способность в 200 единиц продукции за час. Обычная производитель­ность в течение смены, в которой не было простоев, выглядела следу­ющим образом: 1-й час - 198 единиц, 2-й час - 200 ед., 3-й час - 199 ед., 4-й - 200, 5-й - 200. Можно себе представить удивление членов рабочей группы, когда их коллеги стали советовать: «Темп слабоват, вы оставите нас без премиальных». А когда те попытались оправды­ваться, то им заявили: «Посмотрите на статистику. Распределение про­изводительности по часам совсем не похоже на нормальное, на коло­кольчик, это скорее кардиограмма».

8*

Рон Шэдболт, руководитель рабочей группы, незаметно вздохнул. Он считал, что статистика нужна для рекламы и для идиотов из SPC; он никогда не представлял, как ее можно применить на его рабочем месте. Когда он затем вдумался, сколько его ребята и он потеряли и сколько "те другие" получили благодаря переходу от индивидуаль­ных к групповым премиям (бонусам), ему захотелось взвыть.

Price, F. (1984), Right First Time, Aldershot: Guwer Publishing Ltd.

Комментарий

' В уже цитировавшейся в комментариях книге В.Деминга приве­дено множество взятых из жизни примеров использования статисти­ки для решения конкретных управленческих проблем на производ­стве: В. Эдварде Деминг. Выход из кризиса.: Пер. с англ. - Альба: Тверь, 1994.

Закон Зипфа