Расчеты по простым процентам

Автоматизированное вычисление по формулам.

Пусть необходимо производить вычисления по формуле, в которую входят переменные, имеющие определенное смысловое значение. Например, известен начальный размер вклада S₀, процентная ставка p относительно периода начисления, время хранения вклада k, заданное в периодах начисления, и при расчетах используются простые проценты. Необходимо определить размер вклада S_k в момент k. Для расчета используем формулу

S_k= S₀ (1+pk)

Для реализации расчетов на компьютере введем в первый столбец полные имена четырех переменных и выберем пункты меню формат>столбец>автоподбор. Во второй столбец сокращенные обозначения переменных. В третий столбец введем заданные значения трех переменных и присвоим им в качестве имен сокращенные обозначения, выбрав для каждой ячейки в меню пункты вставка >имя> присвоить. В четвертую ячейку третьего столбца введем формулу для расчета, указанную выше.

Задача 1. Выполнить указанные действия на компьютере, если p=0,1; k=5; S₀=100.

Расчеты по простым процентам.

В рассмотренном выше примере ситуация была упрощена. Чтобы сделать расчеты, имеющими практическое значение, обозначим р — годовая ставка процента, m — число периодов начисления за один год. Тогда p/m — годовая ставка, отнесенная к периоду начисления. Заметим, что обычно величина дается в процентах, а в формулах чаще используется в долях, поэтому перед подстановкой в формулу p делим на сто. Например, если годовая ставка составляет 6%, то в формулу подставляется 0,06.

Если отсчет времени начисления начинается с момента внесения вклада и время хранения вклада равно k периодам начисления, то:

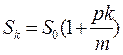, (1)

Если момент внесения вклада совпадает с началом периода начисления, то сумму, начисленную за t единицу времени хранения начисляем по формуле:

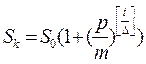, (2)

где скобки [ ] означают взятие целой части числа,
Δ— длительность периода начисления.

Используемые в формуле длительности необходимо задавать в одинаковых единицах времени, учитывая, что обычно в финансовых операциях полагается, что один года равен 360 дням, один месяц равен 30 дням.

Например, если вклад пролежал на депозите 2 года 16 дней, проценты начисляются ежемесячно из расчета 6% годовых, в этом случае t = 736, Δ= 30, m = 12. Следовательно, каждый рубль вклада превратится в (1+(0.06/12)[736/30]) = 1+(0.06/12)24 = 1.12 руб.

Если время хранения, следующее за последним начислением процентов, также учитывается при начислении, то формула (2) упрощается:

S_t= S₀(1+pt/mΔ), (3)

где mΔ= 1 год.

Если t исчисляется в днях, то

S_t= S₀(1+pt/360), (4)

Если исчисление ведется в годах, то

S_t= S₀(1+pt), (5)

Отметим также, что стоимость вклада в формулах (3)—(5) не зависит от длительности периода начисления.

Задача 2. Создать таблицу анализа эффективности депозита при различных процентных ставках. Для этого столбцы озаглавить: процент, 1 год, 2 года, 5 лет, 10 лет. Для процентов выбрать значения от 1 до 51 с шагом 5. Использовать формулу (5), полагая S₀ = 1.

Задача 3. Пусть ссуда в размере 10 000 руб. дана на два года из расчета 22 % годовых. Какую сумму получит заимодавец в конце указанного периода?

Обычно при проведении практических расчетов задают дату внесения вклада d₀ и текущую дату d_t в формате чч.мм.гг. Для расчета будем использовать формулу (4), которую преобразуем к следующему виду:

S_t= S₀(1+p(d_t–d₀)/360), (6)

где d_t–d₀ = день360(нач_дата; кон_дата), (7)

Задача 4. Создать следующую таблицу:

Расчет депозита

Сумма вклада	S0	число_1
Дата вклада	d0	дата _0
Текущая дата	dt	дата _1
Время хранения	t	формула (7)
Процентная ставка	p	число _2
Сумма начисления	St	формула (6)

Введите значения для дат и формулу (7) и проверьте ее работоспособность при различных значениях d₀ и d_t. Далее, используя формулу (6), подсчитайте текущую величину вклада S_t при различных значениях остальных параметров.

В формуле (6) t = dt – d0, поэтому если задать время t, величину начального вклада S0. и величину вклада St в момент t, то можно подсчитать процент р. Для этого воспользуемся формулой (5), и получим формулу 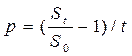(8):

, (8)

Например, пусть нам выдана ссуда S₀ на определенный срок t с условием возврата S_t. Какая процентная ставка обеспечивает выполнение контракта?

Для использования этой формулы необходимо изменить таблицу: вместо формулы (7) записать число дней, а число_2, заменить формулой (8).

Задача 5. Сравнить условия контракта задачи 3 с другим контрактом, по которому через два года возвращается ссуда в 15000 руб.

Используя формулу (5), можно получить современную стоимость денег:

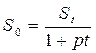, (9)

Эта формула позволяет сравнить контракты с различным сроком действия.

Задача 6. Вычислив современную стоимость денег, сравнить два контракта:
· уплатить 10 тыс. руб. через 5 лет и 5 тыс. руб. через 15 лет;
· уплатить 6 тыс. руб. через 3 года и 8 тыс. руб. через 7 лет.
На деньги начисляется 8% годовых процентов.