Неформализованный анализ обособленного риска проекта. Анализ чувствительности
Метод анализа чувствительности является очень простым и доступным. В данном случае не ставится цель количественно оценить риск. Задача метода — оценить влияние на значение NPV входных параметров в формуле NPV (как изменение условий реализации проекта отразится на значении эффекта). Риск рассматривается как степень чувствительности чистого дисконтированного дохода к изменению условий функционирования (изменению налоговых платежей, ценовым изменениям, изменениям средних переменных издержек и т.п.) Метод анализа чувствительности строит принятие решений на базе ответов на большое число вопросов типа "что будет, если...?" Например, что произойдет, если цена продажи нового продукта упадет на 10%? Будет ли проект эффективным? Какой уровень реализационного дохода (выручки) требуется для получения положительного значения NPV?
Часто метод анализа чувствительности проводится графически или таблично. Показывается процентное изменение результата — чистого дисконтированного дохода (NPV) или внутренней нормы доходности (IRR) — при изменении одного из условий функционирования (другие факторы предполагаются неизменными). Анализ начинается с установления базового значения результата, например ЧДД (NPV), при фиксированных значениях параметров, влияющих на результат оценки проекта.
Например, рассматривается проект строительства завода по производству стеклотары. Инвестиционные затраты осуществляются в течение одного года (2000) и прогнозируются потоки денежных средств по годам, приведенные в табл. 8.3.
Чистый дисконтированный доход по проекту при ставке дисконтирования 20% равен 0,727 млрд. руб.: (-24 + 7,64/ 1,2 + 26,44 / 1,22 = 0,727).
В анализе чувствительности могут рассматриваться следующие факторы, влияющие на значение NPV: объем (количество) продаж, средние переменные издержки, стоимость капитала, налоговые отчисления и т.п.
Зависит ли выбор факторов от направления деятельности, от степени ответственности по проекту, от слаженности команды управленцев?
Таблица 8.3. Оценка денежных потоков для расчета NPV, млрд. руб.
| 2000 г. | 2001 г. | 2002 г. | ||
| Инвестиции: в здание в оборудование в текущие активы | -12 -10 -2 | |||
| Реализационный доход (поступление денежных средств) | ||||
| Переменные издержки (60% от цены) | ||||
| Постоянные издержки | ||||
| Амортизация здания (5%) | 0,6 | 0,6 | ||
| Амортизация оборудования (20%) | ||||
| Налогооблагаемая прибыль | 40 - 24 - 5 - 0,6 - 2 = 8,4 | 8,4 | ||
| Налоговые платежи (40%) | 3,36 | 3.36 | ||
| Чистая прибыль | 8,4 - 3,36 = 5,04 | 5,04 | ||
| Чистый денежный поток, как сумма чистой прибыли и амортизационных отчислений | 5,04 + 2,6 = 7,64 | 7,64 | ||
| Доход от реализации текущих активов по окончании проекта (ликвидация) | ||||
| Доход от продажи внеоборотных активов по остаточной стоимости | 16,8 | |||
| Суммарный чистый денежный поток | -24 | 7,64 | 26,44 | |
Метод анализа чувствительности предполагает расчет изменения NPV при изменении каждого фактора (другие неизменны), например, на 10%. При графическом анализе по оси абсцисс откладывается процентная шкала изменения одного фактора, а по оси ординат — изменение NPV (или IRR). На рис. 8.4 показаны графики чувствительности проекта к изменению объема продаж, средних переменных издержек, стоимости капитала, постоянных издержек. Изменение постоянных затрат приводит к эффекту операционного рычага.
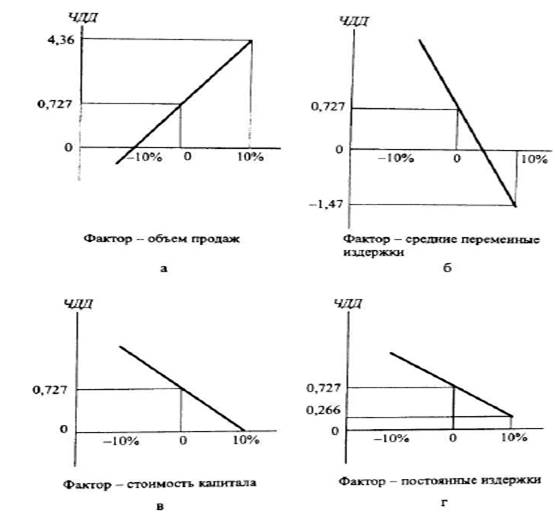
Рис. 8.4. Чувствительность проекта к изменению различных факторов
В базовом варианте ЧДД = 0,727. Увеличение объема продаж на 10% приводит при постоянстве других факторов (прежде всего продажной цены) к росту дохода от реализации до 44 млрд. руб. в первый и второй годы жизни проекта. Чистые денежные потоки по годам составляют 10,04, во втором году с учетом ликвидационного дохода чистый поток составит 28,84 млрд. руб.; ЧДД = 4,36 (рис. 8.4 а).
Чувствительность ЧДД к изменению средних переменных издержек показана на рис. 8.4 б. 10%-й рост средних переменных издержек (на единицу продукции) приведет к росту переменных издержек в первом и втором годах до 26,4 млрд. руб., что повлечет снижение чистого денежного потока по годам и при неизменной ставке дисконтирования 20% приведет к отрицательному значению ЧДД= -1,47.
Чем круче прямая реагирования (чем больше угол ее наклона), тем чувствительнее значение NPV к изменению фактора и больше риск. Общую картину чувствительности можно рассмотреть на графике множества прямых реагирования (рис. 8.5), где на оси ординат показаны значения ЧДД (NPV), а на оси абсцисс — шкала процентных изменений (т.е. изменение на 10, 20% и т.д.). Например, увеличение инвестиционных затрат на 3% приведет к занулению значения ЧДД (NPV).
Пересечение прямой реагирования с осью абсцисс показывает, при каком изменении (рост со знаком плюс, снижение со знаком минус) фактора в процентном выражении проект станет неэффективным.
Сценарный анализ
Хотя метод анализа чувствительности широко используется благодаря своей простоте, имеются ограничения в его применении. Например, если рассматривается проект строительства предприятия по производству стеклотары и метод анализа чувствительности показал, что чистый дисконтированный доход в наибольшей степени реагирует на изменения объема выпуска, средних переменных издержек и цен продаж, то заключение контрактов на продажу фиксированного количества продукции по оговоренной цене с учетом инфляции позволяет гарантировать определенное значение NPV. Однако срыв контракта приведет к ухудшению ситуации и уменьшению фактического значения NPV из-за ценовых изменений, изменений средних переменных издержек и других факторов. В общем случае обособленный риск проекта зависит от: 1) чувствительности NPV проекта к изменению основных факторов риска; 2) взаимосвязанности этих факторов и возможности их совместного влияния на проект. Метод анализа чувствительности рассматривает только первое условие и, таким образом, является неполным.
Сценарный анализ — метод неформализованного описания обособленного риска проекта, включающий оценку чувствительности NPV к изменению факторов и оценку возможности совместного действия факторов. В сценарном анализе особое внимание уделяется:
• наихудшему варианту функционирования проекта, когда негативные факторы накладываются друг на друга и совместно влияют на значение NPV (низкий спрос, низкие продажные цены, высокие средние переменные издержки, рост инвестиционных затрат и т.п.);
• наилучшему варианту функционирования.
Формулирование сценариев (худшего и лучшего) позволяет рассчитать значение NPV по каждому и сравнить с ожидаемым (базовым) значением NPV. Худший сценарий предполагает задание наихудших прогнозируемых значений по всем факторам (если возможно их совместное осуществление). В наилучшем сценарии все факторы задаются наиболее благоприятными из возможных значениями.
Например, в табл. 8.4 построены сценарии и рассчитаны значения NPV по проекту выпуска стеклотары.
Таблица 8.4. Сценарный подход к оценке проекта
| Сценарий | NPV, млрд. руб. | Вероятность, % |
| Наихудший (объем продаж снизится на 2%, средние переменные издержки возрастут на 5%, продажная цена упадет на 1%) | -0,35 | |
| Базовый | 0,727 | |
| Наилучший (повысится объем продаж на 5%, снизятся средние переменные издержки и т.п.) | 2,1 |
По сценарному анализу могут быть рассчитаны ожидаемое значение NPV, стандартное отклонение и коэффициент вариации. Основное требование — задание вероятностного распределения по сценариям, что на практике представляет большую проблему. Ожидаемое значение NPV= -0,35 х 0,25 + 0,727 х 0,5 + 2,1 х 0,25 = 0,801 не равно базовому значению, так как факторы накладываются и сдвигают распределение NPV вправо. Коэффициент вариации по проекту сравнивается с коэффициентами по существующим проектам (средняя оценка), и если коэффициент вариации превышает данный коэффициент по среднему проекту, то делается вывод о большем риске.
Недостатком сценарного анализа является рассмотрение только нескольких возможных исходов по проекту (дискретное множество значений NPV), хотя в действительности число возможных исходов не ограничено. Развитием сценарного метода является имитационный метод.
Метод Монте-Карло
Метод Монте-Карло является методом имитационного моделирования. Впервые он был предложен для оценки риска обособленного инвестиционного проекта в 1964 г. Д. Герцем[16], который описал подход, использовавшийся его консультационной фирмой для оценки проекта расширения производства химического концерна. Идея метода заключается в соединении анализа чувствительности и вероятностных распределений факторов модели. Вместо того чтобы создавать отдельные сценарии (наилучший, наихудший), в имитационном методе компьютер генерирует сотни возможных комбинаций факторов с учетом их вероятностного распределения. Каждая комбинация дает свое значение NPV, и в совокупности аналитик получает вероятностное распределение результата проекта. Факторы, по которым строится вероятностное распределение, приведены в табл. 8.5.
Таблица 8.5. Факторы имитационной модели
| Рыночные факторы | Инвестиционные факторы | Затратные факторы |
| Объем производства по проекту Темп роста производства Продажная цена продукции проекта Доля рынка, на которую нацелен проект | Инвестиционные затраты Срок жизни проекта Ликвидационная стоимость проекта | Переменные издержки Постоянные издержки |
Имитационное моделирование строится по следующей схеме:
1) формулируются факторы;
2) строится вероятностное распределение по каждому фактору;
3) компьютер случайным образом выбирает значение каждого фактора риска, основываясь на вероятностном распределении этого фактора;
4) эти значения факторов риска комбинируются с факторами, по которым не ожидается изменение (например, налоговая ставка или норма амортизации), и рассчитывается значение чистого денежного потока для каждого года. По чистым денежным потокам рассчитывается значение чистого дисконтированного дохода (NPV);
5) действия 3, 4 и 5 повторяются много раз (например, 5UU прогонов), что позволяет построить вероятностное распределение NPV.
При сравнении взаимоисключающих проектов выбор остается за тем, у которого среднее значение NPV больше, а вероятностное распределение имеет более заостренную форму. Так, на рис. 8.6 проект А предпочтительнее проекта В, так как по нему выше значение ЧДД и ниже риск.
На практике очень немногие компании используют метод имитационного моделирования. Причины состоят в следующем:
• описанная модель Герца предполагает, что экономические факторы взаимонезависимы. В действительности, большинство факторов статистически зависимы (например, объем продаж и цена продаваемой продукции). Для включения этих зависимостей в расчет они должны быть оценены. Такие оценки не всегда доступны аналитикам и сильно усложняют модель. При включении в рассмотрение взаимосвязей они должны быть смоделированы вместе;
• модель предполагает знание вероятностных распределений экзогенных факторов. Эти оценки также доступны лишь узкому кругу аналитиков, что не способствует популярности модели.
