Варіанти завдань до лабораторної роботи №3
1. Є|наявний| n міст, зв'язаних мережею|сіттю| шосейних доріг. Відома відстань між містами, якщо вони зв'язані дорогою. Необхідно знайти найкоротший шлях|колію,дорогу| і його довжину від вказаного міста відправлення в будь-яке інше відоме місто (метод Форда визначення найкоротшого шляху|колії,дороги| на графі в інтерпретації Дейкстри). Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Дискретна математика”.
2. Є|наявний| n міст, зв'язаних мережею|сіттю| шосейних доріг. Відома відстань між містами, якщо вони зв'язані дорогою. Необхідно знайти довжини найкоротших шляхів|колій,доріг| між будь-якими двома відомими містами (метод Шимбела визначення найкоротшого шляху|колії,дороги| на графі ). Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Дискретна математика”.
3. “Життя” – це багатоклітинна істота, що населяє прямокутну пустелю. Пустеля розбита на осередки|чарунок,вічка,комірки|, подібні клітинам шахівниці. Осередок|чарунка,вічко,комірка| може бути порожнім|пустим| або вміщати одну клітку|клітину| життя. У цьому світі “життя” розвивається по кроках. За один крок в одних осередках|чарунках,вічках,комірках| клітки|клітини| гинуть, а в інших зароджуються. Зміна поколінь “життя” відбувається|походить| за такими правилами:
- сусідами клітки|клітини| називаються клітки|клітини|, що знаходяться|перебувають| в 8 осередках|чарунках,вічках,комірках|, дотичних з|із| осередком|чарункою,вічком,коміркою|, що містить|утримує| клітку|клітину|;
- якщо клітка|клітина| має двох або трьох сусідів, то вона зберігає себе на наступному|такому| такті “життя”;
- якщо клітка|клітина| має більше трьох або менше двох сусідів – вона гине. У першому випадку – від перенаселеності, в другому – від “самоти|самітності,самотності|”;
- якщо в клітці|клітині| немає “життя”, але|та| у|в,біля| неї рівно три сусідні клітки|клітини|, то в ній зароджується “життя”.
Необхідно написати програму, що дозволяє визначати стан “життя” через вказану кількість кроків. Питання про розміри пустелі і її заповнення вирішити|розв'язати| самостійно.
4. Існує n груп 2-го і 3-го курсів|, які необхідно розподілити в n комп'ютерні класи для проведення лабораторних занять. На основі наявних статистичних досліджень визначена продуктивність кожної групи в кожному комп'ютерному класі. Необхідно так розподілити групи по класах, щоб сумарна продуктивність на заняттях по програмуванню була максимальною (угорський метод рішення задачі вибору: виконати крок приведення масиву і вибір незалежних нулів). Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Методи оптимізації”.
5. Умова завдання|задачі| №4 : реалізувати крок пошуку мінімального покриття матриці і її подальшого|наступного| приведення.
6. Задана “s/t - мережа|сіть|”, яка складається з n міст і m дуг. Необхідно визначити величину максимального потоку в “s/t - мережі|сіті|” (теорема Форда - Фалкерсона). Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Дискретна математика”.
7. Транспортна задача|задача|: вибір початкового опорного рішення|розв'язання,вирішення,розв'язування| методом північно-західного кута|рогу,кутка|. Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Методи оптимізації”.
8. Транспортна задача|задача|: вибір початкового опорного рішення|розв'язання,вирішення,розв'язування| методом мінімального елементу. Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Методи оптимізації” >
9. Транспортна задача|задача|: вибір початкового опорного рішення|розв'язання,вирішення,розв'язування| методом Фогеля. Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Методи оптимізації”.
10. Транспортне задача|задача|: поліпшення|покращання| опорного плану методом потенціалів. Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Методи оптимізації”.
11. Симплексний метод рішення|розв'язання,вирішення,розв'язування| ЗЛП|: побудова|шикування| симплексної таблиці, вибір розв’язуючого елементу. Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Методи оптимізації”.
12. Симплексний метод рішення|розв'язання,вирішення,розв'язування| ЗЛП|: перерахунок симплексної таблиці, визначення оптимальності одержаного|отриманого| рішення|розв'язання,вирішення,розв'язування|. Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Методи оптимізації”.
13. Задані три послідовності: U(розмірності n), X(розмірності m), Y(розмірності r). Враховуючи, що послідовність U – універсальна множина|безліч|, послідовності X і Y – підмножини універсальної множини|безлічі|, необхідно знайти:
- об'єднання множин|безлічі| X і Y;
- перетин множин|безлічі| X і Y;
- різниця множин|безлічі| X і Y, Y і X;
- доповнення множин|безлічі| X і Y;
- прямий добуток|добуток| множин|безлічі| X і Y.
Передбачити можливість|спроможність| некоректного завдання|задавання| множин U, X, Y. Теоретичний матеріал див. в методичних вказівках до виконання семестрової роботи з дисципліні “Дискретна математика”.
14. Задані дві матриці А={aij} розмірності n´n і B={bij} розмірності m´g. Для кожної з них поміняти місцями другий і третій стовпці і елементи рядка, який містить|утримує| найбільший елемент матриці, замінити нулями. Підрахувати|підсумувати| значення найбільшого мінору для матриць А і В.
15. Скласти функцію для обчислення|підрахунку| елементів матриці С={cij}, розмірності m´ g, що є|з'являється,являється| добутком матриць А={aij} розмірності m´ n|добутком| і B={bij} розмірності n´ g. У масиві В поміняти місцями рядки, які вибирає користувач.
16. Скласти функцію для обчислення|підрахунку| елементів матриці С={cij}, яка є сумою матриць А={aij}, |з'являється,являється| і B={bij} розмірності n ´ n. Причому матриця А може бути задана довільно, а елементи матриці B визначаються наступним|слідуючим| чином: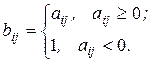 
Потім в матриці А замінити всі від’ємні|заперечні| елементи найменшим в кожному рядку відповідно, а позитивні - замінити залишком|остачею| від ділення|поділки,розподілу,поділу| елементу на 2.
17. Скласти функцію для обчислення|підрахунку| вектора Z={zi}, i=1.m, рівного добутку|добутку| матриці А={aij} розмірності m ´ n на вектор Х={хj}, елементи якого обчислюються за формулою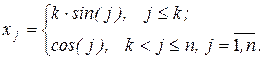 
Перевірити, чи є|з'являються,являються| елементи вектора Z впорядкованими за зменшенням. Якщо ні, то показати перший елемент, що порушив порядок|лад| зменшування, а також номер цього елементу, виправити|справити| порушення, тобто розташувати елементи у порядку|ладі| зменшування.
18. Скласти функцію, яка у заданій|запровадженій| матриці А розмірності m´n знаходить|находить| число R - найменше з|із| позитивних відношень, де s – номер стовпця, в якому елемент ais є негативним|заперечний|. У масиві А замінити елементи стовпця з|із| найменшим значенням нулями.
19. Написати програму, яка будує матрицю А розмірності n´n з|із| компонентами, визначуваними за формулою: aij= sin(i+j)××x, i,j=1.n, x – довільна дійсна величина. Потім в кожному рядку А замінити найбільший елемент абсолютною величиною діагонального елементу, а від’ємні|заперечні| елементи замінити їх кубами. Далі розташувати елементи кожного рядка у порядку|ладі| зростання.
20. У масиві А={aij} розмірності n ´ n знайти різницю між сумою і добутком|добутком| елементів| масиву. Потім в кожному рядку знайти найбільший елемент і упорядкувати всі елементи в правильному порядку|ладі| по відношенню до найбільшого, тобто якщо існує рядок {1.2; 0.5; 7.0; 2.6; 5.0}, то після|потім| впорядкування повинен вийти рядок {0.5; 1.2; 7.0; 5.0; 2.6}.
21. Скласти функцію для обчислення|підрахунку| матриці B={bij}, яка є добутком|добутку| числа g на матрицю А={aij} розмірності n ´ n. Число g – найбільший елемент заданого вектора Z. Потім в матриці В замінити діагональні елементи найбільшими елементами кожного стовпця відповідно.
22. Скласти функцію для обчислення|підрахунку| вектора B={bi}, рівного тому рядку матриці А={aij} розмірності n ´ n, в якій розташований|схильний| найбільший елемент матриці, і вектора С={ci}, який є таким стовпцем матриці А, в якому знаходиться|перебуває| найменший елемент матриці. Потім упорядкувати елементи знайдених векторів| у порядку|ладі| зростання елементів.
23. Задані дві матриці А={aij} розмірності n´n і B={bij} розмірності m´g. Для кожної з них визначити добуток|добуток| від’ємних|заперечних| елементів і їх кількість. Упорядкувати елементи рядків в матриці А і стовпців матриці В у порядку|ладі| зростання лінійним швидким сортуванням.
24. Задано|запроваджена| матрицю А={aij} розмірності m´n. Скласти функцію для побудови|шикування| логічного вектора B={bi} за наступним|слідуючим| правилом: якщо в рядку з|із| номером k кількість позитивних елементів більше ніж кількість від’ємних |заперечних|, то bk=1(true), інакше bk=0(false). Потім необхідно розташувати елементи кожного стовпця масиву А по убуванню лінійним сортуванням.
25. Задано|запроваджена| матрицю А={aij} розмірності n´n. Скласти функцію для побудови|шикування| вектора B={bi} за наступним|слідуючим| правилом: якщо aii<0, то bi прийняти рівним сумі елементів і - ого рядка, інакше – суму абсолютних величин і - го стовпця. Потім в матриці А розташувати елементи кожного рядка у порядку|ладі| зростання.
26. Введена|запроваджена| матриця А={aij} розмірності m´n. Скласти функцію для побудови|шикування| логічного вектора B={bi} за наступним|слідуючим| правилом: якщо і - ий рядок матриці А утворює незбутню послідовність, то bk=1(true), інакше bk=0(false). Потім в матриці А для кожного рядка визначити номери найменших елементів і добуток|добуток| |слідуючих| елементів, що йдуть за ними.
27. Введені|запроваджені| логічний вектор А={ai} і дійсний Х={хi} і=1,., n. Скласти функцію для перетворення вектора Х за правилом: якщо ai=1(true), то хi помножити на 10, інакше – розділити на -10. Потім у векторі Х замінити позитивні елементи найбільшим серед позитивних, а від’ємні|заперечні| – найменшим серед від’ємних |заперечних|.
28. Написати аналог гри “Хрестики - нулі”.
29. Заданий куб 2´2´2, грані якого розбиті на 4 однакових сектори 1´1. Кожний з секторів розфарбований довільним чином. Визначити, чи розфарбована кожна з граней куба одним кольором|цвітом|. Спосіб зберігання даних визначити самостійно.
30. Заданий масив 3´3, заповнений довільно числами від 1 до 8, одна комірка|чарунка,вічко,комірка| масиву “умовно порожня|пустий|”. Використовуючи принцип гри “п’ятнашки”, упорядкувати елементи масиву.
Лабораторна робота № 4
Робота з рядками|
Мета. Отримати тримати практичні навички навички роботи з рядками на С++.
Короткі теоретичні відомості
У С/С++ рядок символів розглядається|розглядується| як звичайний|звичний| масив символів, в якому останнім слідує|прямує| символ закінчення рядка ‘\0’ . При цьому довжина масиву визначається на одиницю більше довжини реального рядка.
Функції обробки рядків описані|перебувають| в модулі string.h. (основні з|із| них див. в додатку А)|посібнику|.
Слід зазначити, що рядок можна розглядати як єдине ціле, а можна використовувати як звичайний масив символів. В останньому випадку необхідно враховувати, що будь - який рядок повинен завершуватися нульовим символом. Всі функції модуля string.h враховують останній нульовий символ рядка автоматично.
Наприклад. Необхідно ввести|запровадити| послідовність рядків довільної довжини і вивести їх на екран.
#include<iostream.h>
#include<string.h>
#include<conio.h>//містить прототипи функцій clrscr() і getch()
#include<process.h>//містить прототип функції exit()
void main()
{ clrscr();
char* str_temp=new char[255]; /* визначаємо буферний рядок, який може містити максимальну кількість символів */
char** m_str;
int i,j,n;
cout<<"\n Введіть кількість рядків ";
cin>>n;
m_str=new char*[n]; /* розподіляємо пам'ять під зберігання адреси кожного
рядка, що вводиться|запроваджується|. Якщо оператор new повертає як адресу NULL, то повідомляємо користувача про помилку і припиняємо роботу функції main() */
if(!m_str){ cerr<<"\n Помилка при розподілі пам’яті";
exit(1);}
cin.ignore(); /* функція-член класу cin, яка ігнорує за умовчанням код символу “Enter”, який було натиснуто при вводі кількості рядків. Функція має два параметри (int, char) – кількість символів ігнорування і символ, який стоїть в кінці|у кінці,наприкінці| цієї послідовності */
for(i=0;i<n;i++)
{ cout<<"\n Введіть "<<i+1<<"-ий рядок ";
cin.getline(str_temp,255); /* функція-член класу cin, яка дозволяє занести
символи з вхідного потоку в змінну str_temp. Другий параметр визначає максимальну довжину рядка.*/
m_str[i]=new char[strlen(str_temp)+1]; /* розподіляємо пам'ять під зберігання рядка, що вводиться|запроваджується| за допомогою буферного рядка. Оскільки функція strlen() визначає довжину рядка без урахування символу нуля, то додаємо|добавляємо| 1 до реального значення довжини рядка, резервуючи місце для символу завершення рядка */
if(!m_str[i]){ cerr<<"\n Помилка при розподілі пам’яті ";
exit(1);}
strcpy(m_str[i],str_temp);}
delete[] str_temp; // звільняємо пам’ять, яку було зайнято буферним рядком
cout<<"\n Масив рядків, який введено\n";
for(i=0;i<n;i++)
{ cout<<m_str[i]<<endl; //виводимо рядок на екран
delete[] m_str[i];} /* звільняємо пам’ять, яка була зайнята під ряжок, який виведено на екран */.
delete[] m_str; /*звільняємо пам’ять, яку було зарезервовано під зберігання масиву адрес рядків */
getch();
}