Концепция эффективности портфеля
Эффективным портфелем (efficient portfolio) мы называем такой портфель, который предлагает инвестору максимально возможный ожидаемый уровень доходности при заданном уровне риска.
Чтобы объяснить значение концепции эффективности портфеля и показать, как получить действительно эффективный портфель, давайте рассмотрим предыдущий пример, дополнительно включив в него еще один рискованный актив. Рискованный актив 2 имеет ожидаемую ставку доходности 0,08 в год и стандартное отклонение 0.15. Он представлен точкой R на рис. 12.2.
Инвестор, который хоче1 получить ожидаемую ставку доходности в 0.08 годовых, может добиться своей цели, вложив всю сумму в рискованный актив 2. Тогда он окажется в ситуации, описываемой точкой R. Но при этом портфель инвестора неэффективен, потому что в точке G инвестор может получить такую же ожидаемую ставку доходности (0,08 в год) при меньшем значении стандартного отклонения.
Из табл. 12.1 видно, что в точке G стандартное отклонение составляет только 0,05. Это объясняется тем, ч-ю 25% инвестиций данного портфеля вложены в рискованный актив 1, а 75% — в безрисковый актив. Действительно, не желающий рисковать инвестор выберет на прямой риск/доходность, соединяющей точки G и S, любую точку — только не точку R. Любая из этих точек соответствует вполне приемлемой ситуации, когда некоторое количество рискованного актива 1 уравновешивается безрисковым активом. Например, портфель в точке J имеет стандартное отклонение, равное стандартному отклонению рискованного актива 2 (о = 0,15), но его ожидаемая ставка доходности составляет 0,12 годовых, а не 0,08. Из табл. 12.1 нам известно, что такое соотношение соответствует портфелю, который на 75% состоит из рискованного актива 1 и на 25% из безрискового актива.
С помощью уравнений 12.1 и 12.2 можно определить состав других эффективных портфелей, которые описываются точками между G и J и имеют, следовательно, более высокую ожидаемую ставку доходности и меньшее значение стандартного oтклонения в сравнении с рискованным активом 2. Рассмотрим, например, портфель, который на 62,5% состоит из рискованного актива 1 и на 37,5 % — безрискового актива. Его ожидаемая ставка доходности равна 0,11 в год, а стандартное отклонение составляет 0,125.
| Контрольный вопрос 12.7 |
| Как инвестор может получить ожидаемую ставку доходности в 0,105 годовых, вложив средства в рискованный актив 1 и безрисковый актив? Каким будет стандартное отклонение такого портфеля? Сравните это значение со стандартным отклонением рискованного актива 2. |
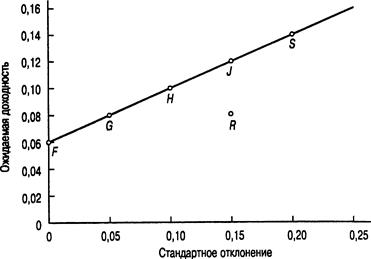
Рис. 12.2. Эффективность портфеля
Примечание. В точке R портфель на 100% состоит из инвестиций, вложенных в рискованный актив 2 с ожидаемой ставкой доходности 0,08 и s = 0,15. Инвестор может получить более высокую ожидаемую доходность и меньшее стандартное отклонение в любой точке прямой, проходящей через точки G и J.
