Основные формулы теории вероятностей
Задача 1. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?
Решение. Событие A={вынуты пуговицы одного цвета} можно представить в виде суммы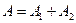 
, где события 
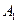и 
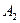означают выбор пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна 
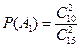, а вероятность вытащить две синие пуговицы 
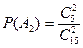. Так как события 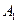и 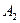не могут произойти одновременно, то в силу теоремы сложения
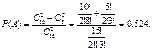
Задача 2. Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий, 42% – французский; английский и немецкий – 8%, английский и французский – 10%, немецкий и французский – 5%, все три языка – 3%. Найти вероятность того, что случайно выбранный сотрудник фирмы: а) знает английский или немецкий; б) знает английский, немецкий или французский; в) не знает ни один из перечисленных языков.
Решение. Обозначим через A, B и С события, заключающиеся в том, что случайно выбранный сотрудник фирмы владеет английским, немецким или французским соответственно. Очевидно, доли сотрудников фирмы, владеющих теми или иными языками, определяют вероятности этих событий. Получаем:
а) P(AÈB)=P(A)+P(B) -P(AB)=0,28+0,3-0,08=0,5;
б) P(AÈBÈC)=P(A)+P(B)+P(C)-(P(AB)+P(AC)+P(BC))+P(ABC)=0,28+0,3+0,42-
-(0,08+0,1+0,05)+0,03=0,8;
в) 1-P(AÈBÈC)=0,2.
Задача 3.В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?
Решение. Пусть А={старший ребенок – мальчик}, B={в семье есть дети обоего пола}. Будем считать, что рождение мальчика и рождение девочки – равновероятные события. Если рождение мальчика обозначить буквой М, а рождение девочки – Д, то пространство всех элементарных исходов состоит из четырех пар: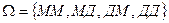 
. В этом пространстве лишь два исхода (МД и ДМ) отвечают событию B. Событие AB означает, что в семье есть дети обоего пола. Старший ребенок – мальчик, следовательно, второй (младший) ребенок – девочка. Этому событию AB отвечает один исход – МД. Таким образом, |AB|=1, |B|=2 и
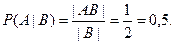
Задача 4. Мастер, имея 10 деталей, из которых 3 – нестандартных, проверяет детали одну за другой, пока ему не попадется стандартная. Какова вероятность, что он проверит ровно две детали?
Решение. Событие А={мастер проверил ровно две детали} означает, что при такой проверке первая деталь оказалась нестандартной, а вторая – стандартная. Значит,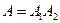 
, где 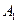={ первая деталь оказалась нестандартной } и 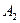={вторая деталь – стандартная}. Очевидно, что вероятность события А1 равна 
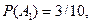кроме того, 
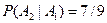, так как перед взятием второй детали у мастера осталось 9 деталей, из которых только 2 нестандартные и 7 стандартных. По теореме умножения
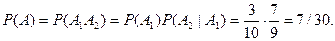
Задача 5.В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.
Решение. Событие A={хотя бы из одного ящика вынут белый шар} можно представить в виде суммы 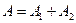, где события 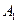и 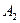означают появление белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна 
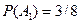, а вероятность вытащить белый шар из второго ящика 
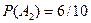. Кроме того, в силу независимост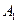и и 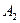имеем: 
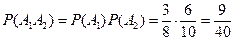. По теореме сложения получаем: 
.
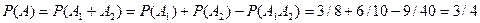Задача 6. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студентов, а третий — 21 студента (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.
Решение. Обозначим через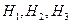 
гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи
, 
, 
.
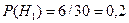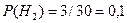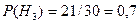Пусть событие A={слабо подготовившийся студент сдал экзамен}. Тогда снова в силу условия задачи
, 
, 
.
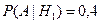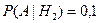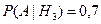По формуле полной вероятности получаем:
.
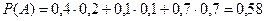Задача 7. Фирма имеет три источника поставки комплектующих – фирмы А, B, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что среди поставляемых фирмой А деталей 10% бракованных, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад деталь окажется годной?
Решение. Пусть событие G – появление годной детали. Вероятности гипотез о том, что деталь поставлена фирмами А, B, С, равны сответственно Р(А)=0,5, Р(В)=0,3, Р(С)=0,2. Условные вероятности появления при этом годной детали равны Р(G|A)=0,9, P(G|B)=0,95, P(G|C)=0,94 (как вероятности противоположных событий к появлению бракованной). По формуле полной вероятности получаем:
P(G)=0,5×0,9+0,3×0,95+0,2×0,94=0,923.
Задача 8 (см. задачу 6). Пусть известно, что студент не сдал экзамен, т.е. получил оценку «неудовлетворительно». Кому из трех преподавателей вероятнее всего он отвечал?
Решение. Вероятность получить «неуд» равна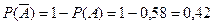 
. Требуется вычислить условные вероятности. По формулам Байеса получаем:
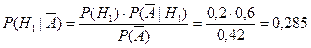, и аналогично,
, 
.
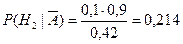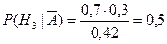Отсюда следует, что, вероятнее всего, слабо подготовившийся студент сдавал экзамен третьему экзаменатору.