Кроме степенных средних в статистике широко используются структурные средние (мода и медиана)
Мода (Мо)– наиболее часто встречающаяся величина признака в рядах распределения.
Пусть задан ряд распределения.
| хi | х1 | х2 | х3 | х4 | х5 |
| fi |
Где хi – значения (вариант) некоторой совокупности (i = 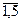 ),
),
fi – частоты (веса) варьирующего признака (i = 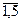 ).
).
Из ряда распределения видим, что наиболее часто встречается (9 раз) варианта х3, поэтому х3 и принимается за среднее значение, т.е. Мо = х3.
Медиана (Ме) – это центральный элемент ранжированного статистического ряда. Ряд называется ранжированным, если его элементы расположены в порядке возрастания или убывания признака.
Пусть статистический ранжированный ряд задан следующим элементами:
х1, х2, … ,хn, тогда:
при n нечетном, т.е. n = 2к+1, Ме= хк+1;
при n четном, т.е. n = 2к Ме=(хк+хк+1)/2, т. е. медиана есть средняя арифметическая величина двух центральных элементов.
Пример 2.Имеются следующие данные процента естественной убыли на некотором предприятии:
| Процент естественной убыли | Количество партий товара |
| 3-5 | |
| 5-7 | |
| 7-9 | |
| 9-11 | |
| Всего |
Определить:
1.Средний процент естественной убыли.
2.Среднеквадратическое отклонение от этой средней.
3.Коэффициент вариации.
4.Модальный интервал.
Для того, чтобы найти среднюю интервального ряда, находим среднюю каждого интервала, равную полусумме верхней и нижней границы интервала, а затем среднюю всего ряда, как среднюю взвешенную. Построим вспомогательную таблицу.
| % естеств. убыли (нижняя граница интервала) | % естеств. убыли (верхняя граница интервала) | Сред няя интер вала хi | Количество партий товара fi | хi × fi | хi - `x | (хi - `x)2 | (хi - `x)2 × fi |
| -3,18 | 10,11 | 151,68 | |||||
| -1,18 | 1,39 | 33,41 | |||||
| 0,82 | 0,67 | 32,27 | |||||
| 2,82 | 7,95 | 103,38 | |||||
| S | 320,76 |
Тогда средний процент естественной убыли определим как среднюю взвешенную
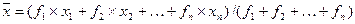 =(15×4+24×6+48×8+13×10)/
=(15×4+24×6+48×8+13×10)/
(15+24+48+13)=718/100=7,18%
Дисперсия процента естественной убыли определяется по формуле D = s2=((4-7,18)2×15+(6-7,18)2×24+(8-7,18)2×48+(10-7,18)2×13)/(15+24+48+13)=320,76/100=3,21
где s - средняя квадратическая взвешенная и находится как корень квадратный из дисперсии, и будет составлять 1,79%.
Коэффициент вариации будет равен:
V=(s/`х )×100%=(1,79/7,18) ×100%=25%
Модальный интервал находится от 7% до 9%, как интервал, имеющий наибольшую частоту партий товара.
Вывод. Из данных 100 партий товара средний процент естественной убыли равен 7,18%; среднеквадратическое отклонение составляет - 1,79%, а коэффициент вариации-25%. Коэффициент вариации показывает, что величина средней характерна для данной совокупности и попадает в модальный иртервал.
Задачи к главе 2
Абсолютные, относительные и средние величины.
Показатели вариации.
Задача 1
В результате выборочного обследования трудового стажа работников по предприятию получены данные:
Везде N – последние две цифры в зачетной книжке.
| Группы работников по стажу работы, лет | Число работников |
| До 5 | 3+N |
| 5-10 | 8+N |
| 10-15 | 20+N |
| 15-20 | 12+N |
| 20 и более | 7+N |
| Итого |
Определите:
1. Средний стаж работы обследуемых работников (выборочную среднюю).
2. Дисперсию и среднее квадратическое отклонение.
3. Коэффициент вариации.
4. Модельный интервал.
Сделать выводы.
Задача 2
За два месяца получены следующие данные о заработной плате продавцов по трем секциям магазина в ден. ед.:
Везде N – последние две цифры в зачетной книжке.
| Секции | Март | Октябрь | ||
| Средняя зарплата | Число продавцов | Средняя зарплата | Фонд оплаты труда | |
| 185+N | 190+N | |||
| 210+N | 220+N | |||
| 198+N | 205+N |
1. Вычислите среднюю месячную заработную плату по трем секциям в целом: а) за март; б) за октябрь.
2. Определить, как изменилась средняя заработная плата в октябре месяце по сравнению с мартом, в абсолютных и относительных измерениях.
3. Укажите, какие формулы средних величин применялись и дайте обоснование к их применению.
Тестовые вопросы к главе 2
