Принципы и методы оценки финансовых инструментов инвестирования

P – рыночная цена, Vt

Финансовый актив, т.е. любая ценная бумага обладает следующими основными характеристиками: цена, стоимость и доходность. Цена стоимость – абсолютные, доходность – относительная. Логика рассуждения инвестора следующая. Если ценная бумага имеет текущую рыночную цену Р, и теоретическую стоимость Vt, которая определяется расчетным путем, то имеются три ситуации.

P > Vt – нет смысла приобретать ценную бумагу, поскольку с позиции инвестора ее рыночная цена завышена

P < Vt – цена занижена, следовательно ценную бумагу целесообразно купить

P = Vt – текущая рыночная цена соответствует теоретической стоимости ценной бумаги, поэтому купля-продажа не целесообразна.

Существуют различные подходы к расчету теоретической стоимости финансового актива. Наиболее распространенным является фундаменталистский подход, который базируется на предположении о том, что теоретическая стоимость любого финансового актива равна дисконтированной стоимости генерируемого им в будущем потока платежей. Согласно этому подходу теоретическая стоимость любой ценной бумаги в общем виде может быть рассчитана по следующей формуле:

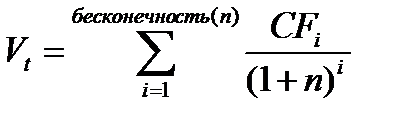(6)

CF_i – ожидаемый денежный поток в i-ом периоде

r – требуемая или альтернативная ставка доходности

Оценка теоретической стоимости зависит от трех основных параметров: ожидаемых денежных поступлений, горизонта прогнозирования или срока владения ценной бумагой и ставки дисконтирования. Первые 2 параметра непосредственно привязаны к финансовому активу, ставка дисконтирования же – это приемлемая норма прибыли, закладываемая инвестором в анализ, которая отражает доходность альтернативных вариантов вложения капитала. Ставка дисконтирования может устанавливаться:

- в размере %% ставки по банковским депозитам

- в размере %% ставки по банковским депозитам + надбавка за риск

- исходя из процентов, выплачиваемых по правительственным облигациям + надбавка за риск

Рассмотрим показатели оценки основных видов облигаций:

- оценка облигаций с нулевым купоном – основана на том, что денежные поступления по годам отсутствуют, поэтому теоретическая стоимость определяется по следующей формуле:

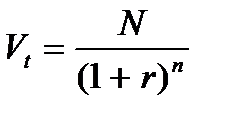(7)

N – номинальная стоимость облигации

n – срок

r – ставка дисконтирования (норма прибыли)

- оценка бессрочной облигации основана на том, что данный вид предусматривает неопределенно долгую выплату дохода в установленном размере или по плавающей процентной ставке:

V_t = С/r (8)

C – выплачиваемый купонный доход

- оценка срочной облигации с фиксированной купонной ставкой основана на том, что денежный поток, генерируемый облигацией представляет собой аннуитет, к которому в конце срока прибавляется дисконтированная номинальная стоимость облигации:

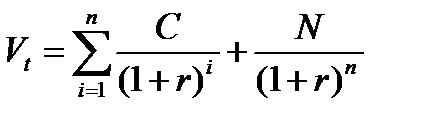(9)

C – совокупный доход

n – срок погашения

Если выплаты осуществляются несколько раз в году, то данная формула трансформируется следующим образом:

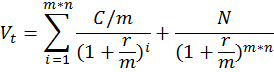
M – количество выплат в году.

Рассмотрим показатели оценки основных видов акций.

Привилегированные акции, как и бессрочные облигации генерируют доход неопределённо долго, поэтому их теоретическая стоимость определяется аналогично как отношение величины дивиденда к рыночным нормам прибыли по акциям данного класса риска:

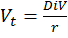(11)

DIV - дивиденды

В некоторых странах привилегированные акции эмитируются на условиях, позволяющих эмитенту выкупить их в определенный момент по соответствующей цене, тогда:

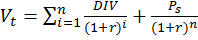(12)

Для оценки обыкновенных акций применяют различные методы. Наиболее распространенный метод – основанный на оценке их будущих поступлений:

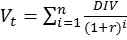(13)

Полученное выражение известно как модель дисконтированных дивидендов, разработанной американским ученым Джоном Уильямсом. Однако данная формула может трансформироваться от динамики дивидендом:

- дивиденды не меняются (применяется формула 11)

- дивиденды возрастают с постоянным темпом прироста

- дивиденды возрастают с изменяющимся темпом прироста

Оценка акций с равномерно возрастающими дивидендами основана на том, что величина последнего выплаченного дивиденда равна С и предполагается, что она ежегодно увеличивается с постоянным темпом прироста g, тогда:

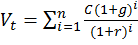(14)

Выполнив математические преобразования можно получить из предыдущей формулы другую, которая называется моделью Гордона:

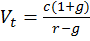(15)

Оценка акций с изменяющимся темпом прироста основана на том, что интервал прогнозирования разбивают на подинтервалы, каждый из которых характеризуется собственным темпом прироста. Т.о. если выделить 2 подинтервала, то:

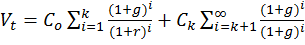(16)

Co – DIV выплаченные в базисный момент времени

Ск – прогноз и DIV в к-периоде

g – прогноз темпов прироста DIVв первый интервал

р – прогноз темпов прироста DIV во второй интервал.